Mass Distribution versus Density Distribution in the Context of Clustering

This paper investigates two fundamental descriptors of data, i.e., density distribution versus mass distribution, in the context of clustering. Density distribution has been the de facto descriptor of data distribution since the introduction of statistics. We show that density distribution has its fundamental limitation -- high-density bias, irrespective of the algorithms used to perform clustering. Existing density-based clustering algorithms have employed different algorithmic means to counter the effect of the high-density bias with some success, but the fundamental limitation of using density distribution remains an obstacle to discovering clusters of arbitrary shapes, sizes and densities. Using the mass distribution as a better foundation, we propose a new algorithm which maximizes the total mass of all clusters, called mass-maximization clustering (MMC). The algorithm can be easily changed to maximize the total density of all clusters in order to examine the fundamental limitation of using density distribution versus mass distribution. The key advantage of the MMC over the density-maximization clustering is that the maximization is conducted without a bias towards dense clusters.

MedRAGChecker: Claim-Level Verification for Biomedical Retrieval-Augmented Generation

Biomedical retrieval-augmented generation (RAG) can ground LLM answers in medical literature, yet long-form outputs often contain isolated unsupported or contradictory claims with safety implications. We introduce MedRAGChecker, a claim-level verification and diagnostic framework for biomedical RAG. Given a question, retrieved evidence, and a generated answer, MedRAGChecker decomposes the answer into atomic claims and estimates claim support by combining evidence-grounded natural language inference (NLI) with biomedical knowledge-graph (KG) consistency signals. Aggregating claim decisions yields answer-level diagnostics that help disentangle retrieval and generation failures, including faithfulness, under-evidence, contradiction, and safety-critical error rates. To enable scalable evaluation, we distill the pipeline into compact biomedical models and use an ensemble verifier with class-specific reliability weighting. Experiments on four biomedical QA benchmarks show that MedRAGChecker reliably flags unsupported and contradicted claims and reveals distinct risk profiles across generators, particularly on safety-critical biomedical relations.

EagleVision: A Dual-Stage Framework with BEV-grounding-based Chain-of-Thought for Spatial Intelligence

Recent spatial intelligence approaches typically attach 3D cues to 2D reasoning pipelines or couple MLLMs with black-box reconstruction modules, leading to weak spatial consistency, limited viewpoint diversity, and evidence chains that cannot be traced back to supporting views. Frameworks for "thinking with images" (e.g., ChatGPT-o3 and DeepEyes) show that stepwise multimodal reasoning can emerge by interleaving hypothesis formation with active acquisition of visual evidence, but they do not address three key challenges in spatial Chain-of-Thought (CoT): building global space perception under strict token budgets, explicitly associating 3D hypotheses with video frames for verification, and designing spatially grounded rewards for reinforcement learning. To address these issues, we present EagleVision, a dual-stage framework for progressive spatial cognition through macro perception and micro verification. In the macro perception stage, EagleVision employs a semantics-perspective-fusion determinantal point process (SPF-DPP) to select a compact set of geometry- and semantics-aware keyframes from long videos under a fixed token budget. In the micro verification stage, we formalize spatial CoT as BEV-grounded pose querying: the agent iteratively predicts poses on a BEV plane, retrieves the nearest real frames, and is trained purely by reinforcement learning with a spatial grounding reward that scores the consistency between predicted poses and observed views. On VSI-Bench, EagleVision achieves state-of-the-art performance among open-source vision-language models, demonstrating strong and generalizable spatial understanding.

Plug-and-Play Clarifier: A Zero-Shot Multimodal Framework for Egocentric Intent Disambiguation

The performance of egocentric AI agents is fundamentally limited by multimodal intent ambiguity. This challenge arises from a combination of underspecified language, imperfect visual data, and deictic gestures, which frequently leads to task failure. Existing monolithic Vision-Language Models (VLMs) struggle to resolve these multimodal ambiguous inputs, often failing silently or hallucinating responses. To address these ambiguities, we introduce the Plug-and-Play Clarifier, a zero-shot and modular framework that decomposes the problem into discrete, solvable sub-tasks. Specifically, our framework consists of three synergistic modules: (1) a text clarifier that uses dialogue-driven reasoning to interactively disambiguate linguistic intent, (2) a vision clarifier that delivers real-time guidance feedback, instructing users to adjust their positioning for improved capture quality, and (3) a cross-modal clarifier with grounding mechanism that robustly interprets 3D pointing gestures and identifies the specific objects users are pointing to. Extensive experiments demonstrate that our framework improves the intent clarification performance of small language models (4--8B) by approximately 30%, making them competitive with significantly larger counterparts. We also observe consistent gains when applying our framework to these larger models. Furthermore, our vision clarifier increases corrective guidance accuracy by over 20%, and our cross-modal clarifier improves semantic answer accuracy for referential grounding by 5%. Overall, our method provides a plug-and-play framework that effectively resolves multimodal ambiguity and significantly enhances user experience in egocentric interaction.

LLMBisect: Breaking Barriers in Bug Bisection with A Comparative Analysis Pipeline

Bug bisection has been an important security task that aims to understand the range of software versions impacted by a bug, i.e., identifying the commit that introduced the bug. However, traditional patch-based bisection methods are faced with several significant barriers: For example, they assume that the bug-inducing commit (BIC) and the patch commit modify the same functions, which is not always true. They often rely solely on code changes, while the commit message frequently contains a wealth of vulnerability-related information. They are also based on simple heuristics (e.g., assuming the BIC initializes lines deleted in the patch) and lack any logical analysis of the vulnerability. In this paper, we make the observation that Large Language Models (LLMs) are well-positioned to break the barriers of existing solutions, e.g., comprehend both textual data and code in patches and commits. Unlike previous BIC identification approaches, which yield poor results, we propose a comprehensive multi-stage pipeline that leverages LLMs to: (1) fully utilize patch information, (2) compare multiple candidate commits in context, and (3) progressively narrow down the candidates through a series of down-selection steps. In our evaluation, we demonstrate that our approach achieves significantly better accuracy than the state-of-the-art solution by more than 38\%. Our results further confirm that the comprehensive multi-stage pipeline is essential, as it improves accuracy by 60\% over a baseline LLM-based bisection method.

MSRepaint: Multiple Sclerosis Repaint with Conditional Denoising Diffusion Implicit Model for Bidirectional Lesion Filling and Synthesis

In multiple sclerosis, lesions interfere with automated magnetic resonance imaging analyses such as brain parcellation and deformable registration, while lesion segmentation models are hindered by the limited availability of annotated training data. To address both issues, we propose MSRepaint, a unified diffusion-based generative model for bidirectional lesion filling and synthesis that restores anatomical continuity for downstream analyses and augments segmentation through realistic data generation. MSRepaint conditions on spatial lesion masks for voxel-level control, incorporates contrast dropout to handle missing inputs, integrates a repainting mechanism to preserve surrounding anatomy during lesion filling and synthesis, and employs a multi-view DDIM inversion and fusion pipeline for 3D consistency with fast inference. Extensive evaluations demonstrate the effectiveness of MSRepaint across multiple tasks. For lesion filling, we evaluate both the accuracy within the filled regions and the impact on downstream tasks including brain parcellation and deformable registration. MSRepaint outperforms the traditional lesion filling methods FSL and NiftySeg, and achieves accuracy on par with FastSurfer-LIT, a recent diffusion model-based inpainting method, while offering over 20 times faster inference. For lesion synthesis, state-of-the-art MS lesion segmentation models trained on MSRepaint-synthesized data outperform those trained on CarveMix-synthesized data or real ISBI challenge training data across multiple benchmarks, including the MICCAI 2016 and UMCL datasets. Additionally, we demonstrate that MSRepaint's unified bidirectional filling and synthesis capability, with full spatial control over lesion appearance, enables high-fidelity simulation of lesion evolution in longitudinal MS progression.

UniMapGen: A Generative Framework for Large-Scale Map Construction from Multi-modal Data

Large-scale map construction is foundational for critical applications such as autonomous driving and navigation systems. Traditional large-scale map construction approaches mainly rely on costly and inefficient special data collection vehicles and labor-intensive annotation processes. While existing satellite-based methods have demonstrated promising potential in enhancing the efficiency and coverage of map construction, they exhibit two major limitations: (1) inherent drawbacks of satellite data (e.g., occlusions, outdatedness) and (2) inefficient vectorization from perception-based methods, resulting in discontinuous and rough roads that require extensive post-processing. This paper presents a novel generative framework, UniMapGen, for large-scale map construction, offering three key innovations: (1) representing lane lines as \textbf{discrete sequence} and establishing an iterative strategy to generate more complete and smooth map vectors than traditional perception-based methods. (2) proposing a flexible architecture that supports \textbf{multi-modal} inputs, enabling dynamic selection among BEV, PV, and text prompt, to overcome the drawbacks of satellite data. (3) developing a \textbf{state update} strategy for global continuity and consistency of the constructed large-scale map. UniMapGen achieves state-of-the-art performance on the OpenSatMap dataset. Furthermore, UniMapGen can infer occluded roads and predict roads missing from dataset annotations. Our code will be released.

Ideal Registration? Segmentation is All You Need

Deep learning has revolutionized image registration by its ability to handle diverse tasks while achieving significant speed advantages over conventional approaches. Current approaches, however, often employ globally uniform smoothness constraints that fail to accommodate the complex, regionally varying deformations characteristic of anatomical motion. To address this limitation, we propose SegReg, a Segmentation-driven Registration framework that implements anatomically adaptive regularization by exploiting region-specific deformation patterns. Our SegReg first decomposes input moving and fixed images into anatomically coherent subregions through segmentation. These localized domains are then processed by the same registration backbone to compute optimized partial deformation fields, which are subsequently integrated into a global deformation field. SegReg achieves near-perfect structural alignment (98.23% Dice on critical anatomies) using ground-truth segmentation, and outperforms existing methods by 2-12% across three clinical registration scenarios (cardiac, abdominal, and lung images) even with automatic segmentation. Our SegReg demonstrates a near-linear dependence of registration accuracy on segmentation quality, transforming the registration challenge into a segmentation problem. The source code will be released upon manuscript acceptance.

Gaussian Primitive Optimized Deformable Retinal Image Registration

Deformable retinal image registration is notoriously difficult due to large homogeneous regions and sparse but critical vascular features, which cause limited gradient signals in standard learning-based frameworks. In this paper, we introduce Gaussian Primitive Optimization (GPO), a novel iterative framework that performs structured message passing to overcome these challenges. After an initial coarse alignment, we extract keypoints at salient anatomical structures (e.g., major vessels) to serve as a minimal set of descriptor-based control nodes (DCN). Each node is modelled as a Gaussian primitive with trainable position, displacement, and radius, thus adapting its spatial influence to local deformation scales. A K-Nearest Neighbors (KNN) Gaussian interpolation then blends and propagates displacement signals from these information-rich nodes to construct a globally coherent displacement field; focusing interpolation on the top (K) neighbors reduces computational overhead while preserving local detail. By strategically anchoring nodes in high-gradient regions, GPO ensures robust gradient flow, mitigating vanishing gradient signal in textureless areas. The framework is optimized end-to-end via a multi-term loss that enforces both keypoint consistency and intensity alignment. Experiments on the FIRE dataset show that GPO reduces the target registration error from 6.2\,px to ~2.4\,px and increases the AUC at 25\,px from 0.770 to 0.938, substantially outperforming existing methods. The source code can be accessed via https://github.com/xintian-99/GPOreg.

PepThink-R1: LLM for Interpretable Cyclic Peptide Optimization with CoT SFT and Reinforcement Learning

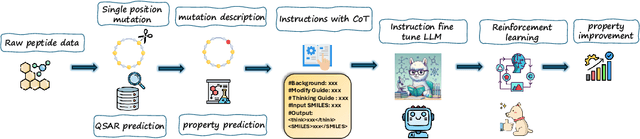
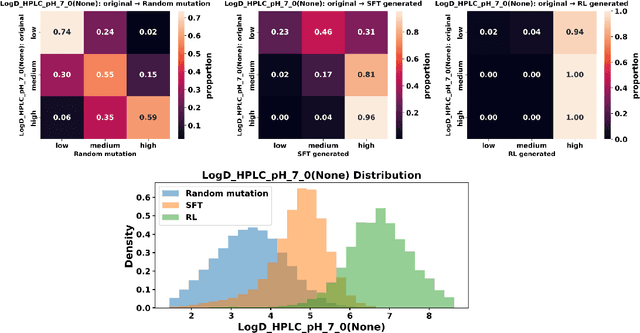
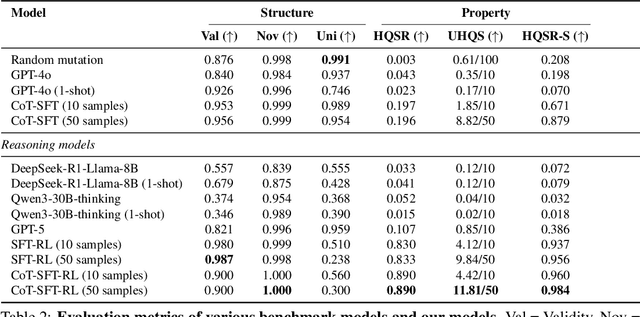
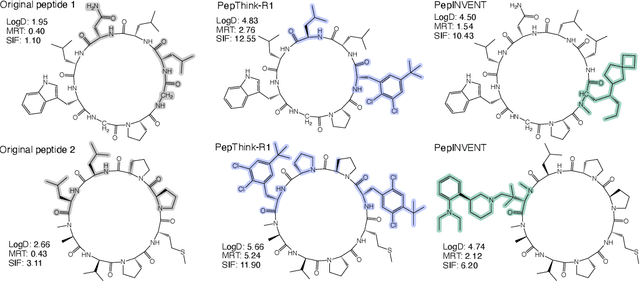
Designing therapeutic peptides with tailored properties is hindered by the vastness of sequence space, limited experimental data, and poor interpretability of current generative models. To address these challenges, we introduce PepThink-R1, a generative framework that integrates large language models (LLMs) with chain-of-thought (CoT) supervised fine-tuning and reinforcement learning (RL). Unlike prior approaches, PepThink-R1 explicitly reasons about monomer-level modifications during sequence generation, enabling interpretable design choices while optimizing for multiple pharmacological properties. Guided by a tailored reward function balancing chemical validity and property improvements, the model autonomously explores diverse sequence variants. We demonstrate that PepThink-R1 generates cyclic peptides with significantly enhanced lipophilicity, stability, and exposure, outperforming existing general LLMs (e.g., GPT-5) and domain-specific baseline in both optimization success and interpretability. To our knowledge, this is the first LLM-based peptide design framework that combines explicit reasoning with RL-driven property control, marking a step toward reliable and transparent peptide optimization for therapeutic discovery.