Biwei Huang
ToolGym: an Open-world Tool-using Environment for Scalable Agent Testing and Data Curation
Jan 09, 2026Abstract:Tool-using LLM agents still struggle in open-world settings with large tool pools, long-horizon objectives, wild constraints, and unreliable tool states. For scalable and realistic training and testing, we introduce an open-world tool-using environment, built on 5,571 format unified tools across 204 commonly used apps. It includes a task creation engine that synthesizes long-horizon, multi-tool workflows with wild constraints, and a state controller that injects interruptions and failures to stress-test robustness. On top of this environment, we develop a tool select-then-execute agent framework with a planner-actor decomposition to separate deliberate reasoning and self-correction from step-wise execution. Comprehensive evaluation of state-of-the-art LLMs reveals the misalignment between tool planning and execution abilities, the constraint following weakness of existing LLMs, and DeepSeek-v3.2's strongest robustness. Finally, we collect 1,170 trajectories from our environment to fine-tune LLMs, achieving superior performance to baselines using 119k samples, indicating the environment's value as both a realistic benchmark and a data engine for tool-using agents. Our code and data will be publicly released.
Transformer Is Inherently a Causal Learner
Jan 09, 2026Abstract:We reveal that transformers trained in an autoregressive manner naturally encode time-delayed causal structures in their learned representations. When predicting future values in multivariate time series, the gradient sensitivities of transformer outputs with respect to past inputs directly recover the underlying causal graph, without any explicit causal objectives or structural constraints. We prove this connection theoretically under standard identifiability conditions and develop a practical extraction method using aggregated gradient attributions. On challenging cases such as nonlinear dynamics, long-term dependencies, and non-stationary systems, this approach greatly surpasses the performance of state-of-the-art discovery algorithms, especially as data heterogeneity increases, exhibiting scaling potential where causal accuracy improves with data volume and heterogeneity, a property traditional methods lack. This unifying view lays the groundwork for a future paradigm where causal discovery operates through the lens of foundation models, and foundation models gain interpretability and enhancement through the lens of causality.
DEPTH: Hallucination-Free Relation Extraction via Dependency-Aware Sentence Simplification and Two-tiered Hierarchical Refinement
Aug 20, 2025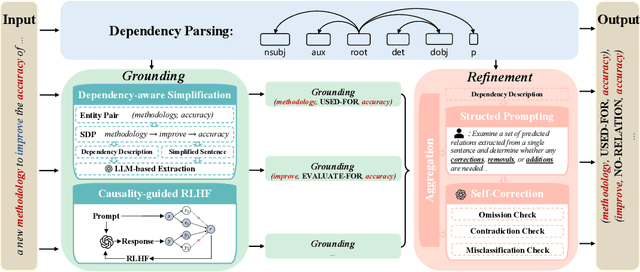

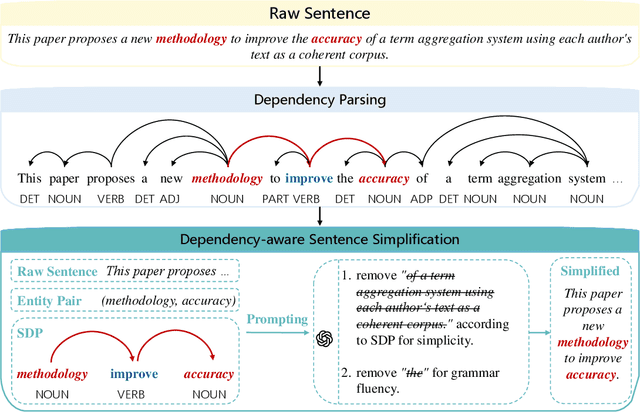

Abstract:Relation extraction enables the construction of structured knowledge for many downstream applications. While large language models (LLMs) have shown great promise in this domain, most existing methods concentrate on relation classification, which predicts the semantic relation type between a related entity pair. However, we observe that LLMs often struggle to reliably determine whether a relation exists, especially in cases involving complex sentence structures or intricate semantics, which leads to spurious predictions. Such hallucinations can introduce noisy edges in knowledge graphs, compromising the integrity of structured knowledge and downstream reliability. To address these challenges, we propose DEPTH, a framework that integrates Dependency-aware sEntence simPlification and Two-tiered Hierarchical refinement into the relation extraction pipeline. Given a sentence and its candidate entity pairs, DEPTH operates in two stages: (1) the Grounding module extracts relations for each pair by leveraging their shortest dependency path, distilling the sentence into a minimal yet coherent relational context that reduces syntactic noise while preserving key semantics; (2) the Refinement module aggregates all local predictions and revises them based on a holistic understanding of the sentence, correcting omissions and inconsistencies. We further introduce a causality-driven reward model that mitigates reward hacking by disentangling spurious correlations, enabling robust fine-tuning via reinforcement learning with human feedback. Experiments on six benchmarks demonstrate that DEPTH reduces the average hallucination rate to 7.0\% while achieving a 17.2\% improvement in average F1 score over state-of-the-art baselines.
Towards General Continuous Memory for Vision-Language Models
May 23, 2025



Abstract:Language models (LMs) and their extension, vision-language models (VLMs), have achieved remarkable performance across various tasks. However, they still struggle with complex reasoning tasks that require multimodal or multilingual real-world knowledge. To support such capabilities, an external memory system that can efficiently provide relevant multimodal information is essential. Existing approaches generally concatenate image and text tokens into a long sequence as memory, which, however, may drastically increase context length and even degrade performance. In contrast, we propose using continuous memory, a compact set of dense embeddings to more effectively and efficiently represent multimodal and multilingual knowledge. Our key insight is that a VLM can serve as its own continuous memory encoder. We empirically show that this design improves performance on complex multimodal reasoning tasks. Building on this, we introduce a data-efficient and parameter-efficient method to fine-tune the VLM into a memory encoder, requiring only 1.2% of the model's parameters and a small corpus of 15.6K self-synthesized samples. Our approach CoMEM utilizes VLM's original capabilities to encode arbitrary multimodal and multilingual knowledge into just 8 continuous embeddings. Since the inference-time VLM remains frozen, our memory module is plug-and-play and can be flexibly integrated as needed. Extensive experiments across eight multimodal reasoning benchmarks demonstrate the effectiveness of our approach.
Activation Control for Efficiently Eliciting Long Chain-of-thought Ability of Language Models
May 23, 2025Abstract:Despite the remarkable reasoning performance, eliciting the long chain-of-thought (CoT) ability in large language models (LLMs) typically requires costly reinforcement learning or supervised fine-tuning on high-quality distilled data. We investigate the internal mechanisms behind this capability and show that a small set of high-impact activations in the last few layers largely governs long-form reasoning attributes, such as output length and self-reflection. By simply amplifying these activations and inserting "wait" tokens, we can invoke the long CoT ability without any training, resulting in significantly increased self-reflection rates and accuracy. Moreover, we find that the activation dynamics follow predictable trajectories, with a sharp rise after special tokens and a subsequent exponential decay. Building on these insights, we introduce a general training-free activation control technique. It leverages a few contrastive examples to identify key activations, and employs simple analytic functions to modulate their values at inference time to elicit long CoTs. Extensive experiments confirm the effectiveness of our method in efficiently eliciting long CoT reasoning in LLMs and improving their performance. Additionally, we propose a parameter-efficient fine-tuning method that trains only a last-layer activation amplification module and a few LoRA layers, outperforming full LoRA fine-tuning on reasoning benchmarks with significantly fewer parameters. Our code and data are publicly released.
A Fast Kernel-based Conditional Independence test with Application to Causal Discovery
May 16, 2025Abstract:Kernel-based conditional independence (KCI) testing is a powerful nonparametric method commonly employed in causal discovery tasks. Despite its flexibility and statistical reliability, cubic computational complexity limits its application to large datasets. To address this computational bottleneck, we propose \textit{FastKCI}, a scalable and parallelizable kernel-based conditional independence test that utilizes a mixture-of-experts approach inspired by embarrassingly parallel inference techniques for Gaussian processes. By partitioning the dataset based on a Gaussian mixture model over the conditioning variables, FastKCI conducts local KCI tests in parallel, aggregating the results using an importance-weighted sampling scheme. Experiments on synthetic datasets and benchmarks on real-world production data validate that FastKCI maintains the statistical power of the original KCI test while achieving substantial computational speedups. FastKCI thus represents a practical and efficient solution for conditional independence testing in causal inference on large-scale data.
Modeling Unseen Environments with Language-guided Composable Causal Components in Reinforcement Learning
May 13, 2025Abstract:Generalization in reinforcement learning (RL) remains a significant challenge, especially when agents encounter novel environments with unseen dynamics. Drawing inspiration from human compositional reasoning -- where known components are reconfigured to handle new situations -- we introduce World Modeling with Compositional Causal Components (WM3C). This novel framework enhances RL generalization by learning and leveraging compositional causal components. Unlike previous approaches focusing on invariant representation learning or meta-learning, WM3C identifies and utilizes causal dynamics among composable elements, facilitating robust adaptation to new tasks. Our approach integrates language as a compositional modality to decompose the latent space into meaningful components and provides theoretical guarantees for their unique identification under mild assumptions. Our practical implementation uses a masked autoencoder with mutual information constraints and adaptive sparsity regularization to capture high-level semantic information and effectively disentangle transition dynamics. Experiments on numerical simulations and real-world robotic manipulation tasks demonstrate that WM3C significantly outperforms existing methods in identifying latent processes, improving policy learning, and generalizing to unseen tasks.
Causal-Copilot: An Autonomous Causal Analysis Agent
Apr 21, 2025Abstract:Causal analysis plays a foundational role in scientific discovery and reliable decision-making, yet it remains largely inaccessible to domain experts due to its conceptual and algorithmic complexity. This disconnect between causal methodology and practical usability presents a dual challenge: domain experts are unable to leverage recent advances in causal learning, while causal researchers lack broad, real-world deployment to test and refine their methods. To address this, we introduce Causal-Copilot, an autonomous agent that operationalizes expert-level causal analysis within a large language model framework. Causal-Copilot automates the full pipeline of causal analysis for both tabular and time-series data -- including causal discovery, causal inference, algorithm selection, hyperparameter optimization, result interpretation, and generation of actionable insights. It supports interactive refinement through natural language, lowering the barrier for non-specialists while preserving methodological rigor. By integrating over 20 state-of-the-art causal analysis techniques, our system fosters a virtuous cycle -- expanding access to advanced causal methods for domain experts while generating rich, real-world applications that inform and advance causal theory. Empirical evaluations demonstrate that Causal-Copilot achieves superior performance compared to existing baselines, offering a reliable, scalable, and extensible solution that bridges the gap between theoretical sophistication and real-world applicability in causal analysis. A live interactive demo of Causal-Copilot is available at https://causalcopilot.com/.
Analytic DAG Constraints for Differentiable DAG Learning
Mar 24, 2025



Abstract:Recovering the underlying Directed Acyclic Graph (DAG) structures from observational data presents a formidable challenge, partly due to the combinatorial nature of the DAG-constrained optimization problem. Recently, researchers have identified gradient vanishing as one of the primary obstacles in differentiable DAG learning and have proposed several DAG constraints to mitigate this issue. By developing the necessary theory to establish a connection between analytic functions and DAG constraints, we demonstrate that analytic functions from the set $\{f(x) = c_0 + \sum_{i=1}^{\infty}c_ix^i | \forall i > 0, c_i > 0; r = \lim_{i\rightarrow \infty}c_{i}/c_{i+1} > 0\}$ can be employed to formulate effective DAG constraints. Furthermore, we establish that this set of functions is closed under several functional operators, including differentiation, summation, and multiplication. Consequently, these operators can be leveraged to create novel DAG constraints based on existing ones. Using these properties, we design a series of DAG constraints and develop an efficient algorithm to evaluate them. Experiments in various settings demonstrate that our DAG constraints outperform previous state-of-the-art comparators. Our implementation is available at https://github.com/zzhang1987/AnalyticDAGLearning.
* Accepted to ICLR 2025
I Predict Therefore I Am: Is Next Token Prediction Enough to Learn Human-Interpretable Concepts from Data?
Mar 12, 2025Abstract:The remarkable achievements of large language models (LLMs) have led many to conclude that they exhibit a form of intelligence. This is as opposed to explanations of their capabilities based on their ability to perform relatively simple manipulations of vast volumes of data. To illuminate the distinction between these explanations, we introduce a novel generative model that generates tokens on the basis of human interpretable concepts represented as latent discrete variables. Under mild conditions, even when the mapping from the latent space to the observed space is non-invertible, we establish an identifiability result: the representations learned by LLMs through next-token prediction can be approximately modeled as the logarithm of the posterior probabilities of these latent discrete concepts, up to an invertible linear transformation. This theoretical finding not only provides evidence that LLMs capture underlying generative factors, but also strongly reinforces the linear representation hypothesis, which posits that LLMs learn linear representations of human-interpretable concepts. Empirically, we validate our theoretical results through evaluations on both simulation data and the Pythia, Llama, and DeepSeek model families.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge