Learning Smooth Humanoid Locomotion through Lipschitz-Constrained Policies

Reinforcement learning combined with sim-to-real transfer offers a general framework for developing locomotion controllers for legged robots. To facilitate successful deployment in the real world, smoothing techniques, such as low-pass filters and smoothness rewards, are often employed to develop policies with smooth behaviors. However, because these techniques are non-differentiable and usually require tedious tuning of a large set of hyperparameters, they tend to require extensive manual tuning for each robotic platform. To address this challenge and establish a general technique for enforcing smooth behaviors, we propose a simple and effective method that imposes a Lipschitz constraint on a learned policy, which we refer to as Lipschitz-Constrained Policies (LCP). We show that the Lipschitz constraint can be implemented in the form of a gradient penalty, which provides a differentiable objective that can be easily incorporated with automatic differentiation frameworks. We demonstrate that LCP effectively replaces the need for smoothing rewards or low-pass filters and can be easily integrated into training frameworks for many distinct humanoid robots. We extensively evaluate LCP in both simulation and real-world humanoid robots, producing smooth and robust locomotion controllers. All simulation and deployment code, along with complete checkpoints, is available on our project page: https://lipschitz-constrained-policy.github.io.

SMT-Based Dynamic Multi-Robot Task Allocation

Multi-Robot Task Allocation (MRTA) is a problem that arises in many application domains including package delivery, warehouse robotics, and healthcare. In this work, we consider the problem of MRTA for a dynamic stream of tasks with task deadlines and capacitated agents (capacity for more than one simultaneous task). Previous work commonly focuses on the static case, uses specialized algorithms for restrictive task specifications, or lacks guarantees. We propose an approach to Dynamic MRTA for capacitated robots that is based on Satisfiability Modulo Theories (SMT) solving and addresses these concerns. We show our approach is both sound and complete, and that the SMT encoding is general, enabling extension to a broader class of task specifications. We show how to leverage the incremental solving capabilities of SMT solvers, keeping learned information when allocating new tasks arriving online, and to solve non-incrementally, which we provide runtime comparisons of. Additionally, we provide an algorithm to start with a smaller but potentially incomplete encoding that can iteratively be adjusted to the complete encoding. We evaluate our method on a parameterized set of benchmarks encoding multi-robot delivery created from a graph abstraction of a hospital-like environment. The effectiveness of our approach is demonstrated using a range of encodings, including quantifier-free theories of uninterpreted functions and linear or bitvector arithmetic across multiple solvers.

Role of Uncertainty in Anticipatory Trajectory Prediction for a Ping-Pong Playing Robot

Robotic interaction in fast-paced environments presents a substantial challenge, particularly in tasks requiring the prediction of dynamic, non-stationary objects for timely and accurate responses. An example of such a task is ping-pong, where the physical limitations of a robot may prevent it from reaching its goal in the time it takes the ball to cross the table. The scene of a ping-pong match contains rich visual information of a player's movement that can allow future game state prediction, with varying degrees of uncertainty. To this aim, we present a visual modeling, prediction, and control system to inform a ping-pong playing robot utilizing visual model uncertainty to allow earlier motion of the robot throughout the game. We present demonstrations and metrics in simulation to show the benefit of incorporating model uncertainty, the limitations of current standard model uncertainty estimators, and the need for more verifiable model uncertainty estimation. Our code is publicly available.

DEC-LOS-RRT: Decentralized Path Planning for Multi-robot Systems with Line-of-sight Constrained Communication

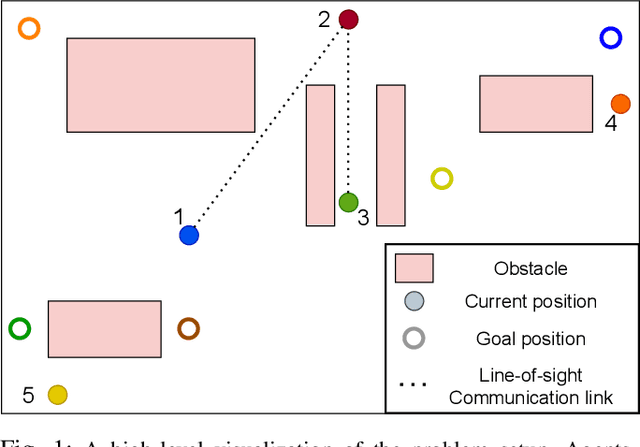
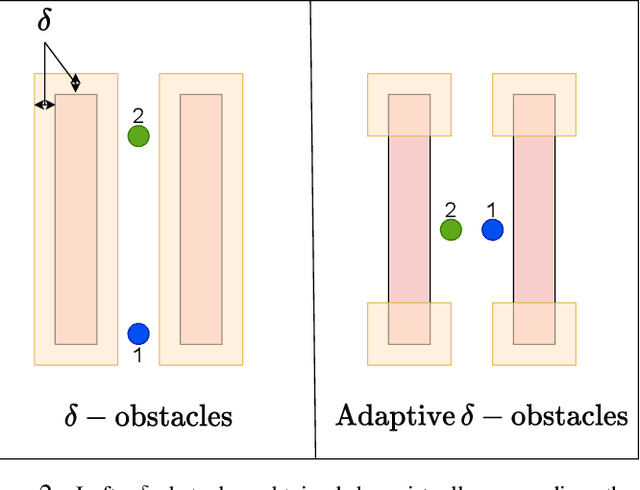
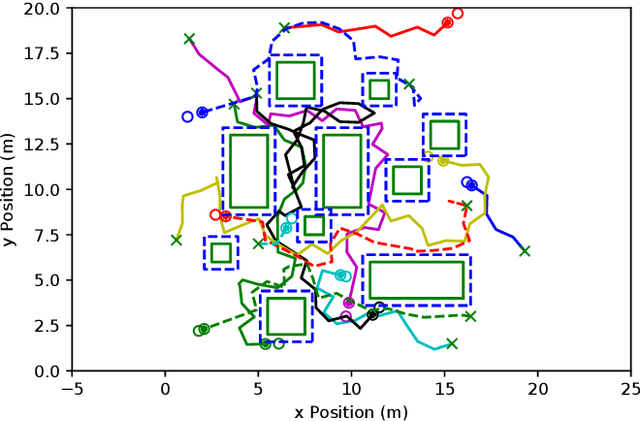
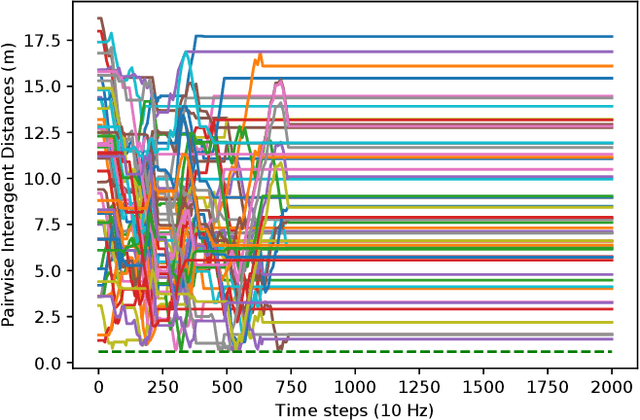
Decentralized planning for multi-agent systems, such as fleets of robots in a search-and-rescue operation, is often constrained by limitations on how agents can communicate with each other. One such limitation is the case when agents can communicate with each other only when they are in line-of-sight (LOS). Developing decentralized planning methods that guarantee safety is difficult in this case, as agents that are occluded from each other might not be able to communicate until it's too late to avoid a safety violation. In this paper, we develop a decentralized planning method that explicitly avoids situations where lack of visibility of other agents would lead to an unsafe situation. Building on top of an existing Rapidly-exploring Random Tree (RRT)-based approach, our method guarantees safety at each iteration. Simulation studies show the effectiveness of our method and compare the degradation in performance with respect to a clairvoyant decentralized planning algorithm where agents can communicate despite not being in LOS of each other.

Who Leads and Who Follows in Strategic Classification?

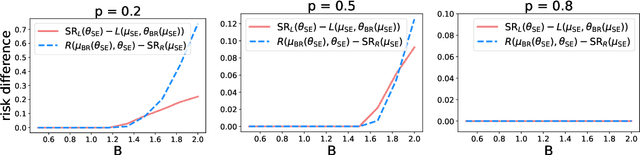
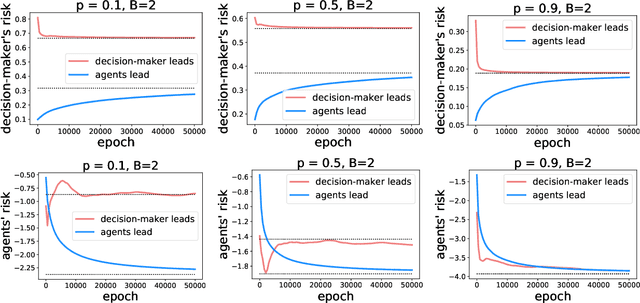
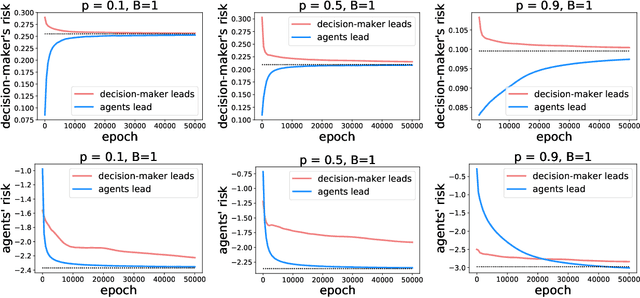
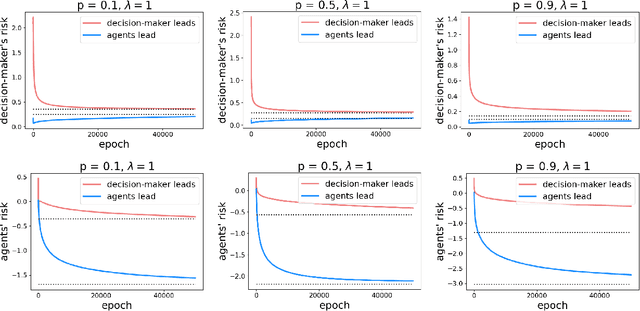
As predictive models are deployed into the real world, they must increasingly contend with strategic behavior. A growing body of work on strategic classification treats this problem as a Stackelberg game: the decision-maker "leads" in the game by deploying a model, and the strategic agents "follow" by playing their best response to the deployed model. Importantly, in this framing, the burden of learning is placed solely on the decision-maker, while the agents' best responses are implicitly treated as instantaneous. In this work, we argue that the order of play in strategic classification is fundamentally determined by the relative frequencies at which the decision-maker and the agents adapt to each other's actions. In particular, by generalizing the standard model to allow both players to learn over time, we show that a decision-maker that makes updates faster than the agents can reverse the order of play, meaning that the agents lead and the decision-maker follows. We observe in standard learning settings that such a role reversal can be desirable for both the decision-maker and the strategic agents. Finally, we show that a decision-maker with the freedom to choose their update frequency can induce learning dynamics that converge to Stackelberg equilibria with either order of play.

Zeroth-Order Methods for Convex-Concave Minmax Problems: Applications to Decision-Dependent Risk Minimization

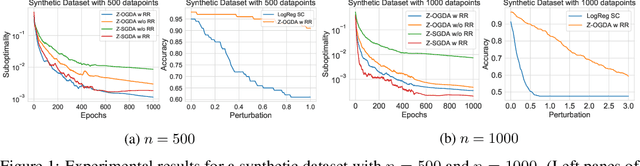
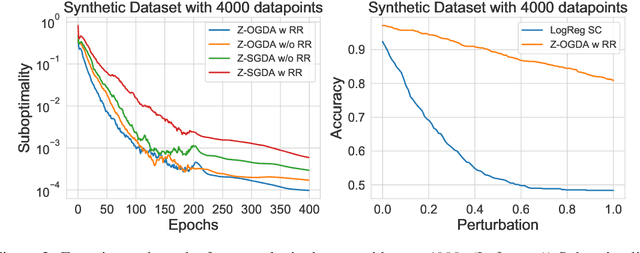
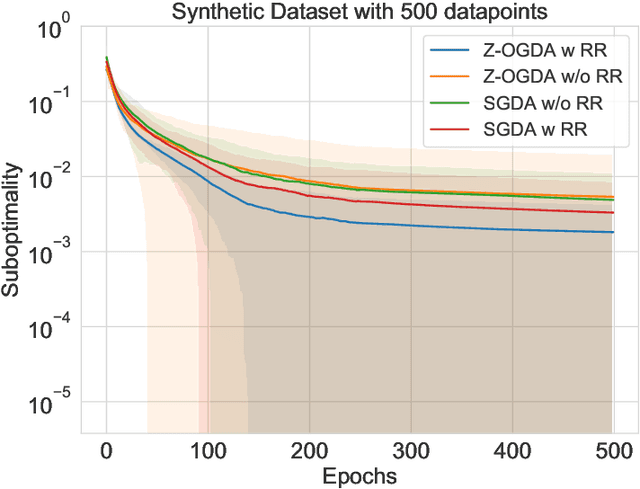
Min-max optimization is emerging as a key framework for analyzing problems of robustness to strategically and adversarially generated data. We propose a random reshuffling-based gradient free Optimistic Gradient Descent-Ascent algorithm for solving convex-concave min-max problems with finite sum structure. We prove that the algorithm enjoys the same convergence rate as that of zeroth-order algorithms for convex minimization problems. We further specialize the algorithm to solve distributionally robust, decision-dependent learning problems, where gradient information is not readily available. Through illustrative simulations, we observe that our proposed approach learns models that are simultaneously robust against adversarial distribution shifts and strategic decisions from the data sources, and outperforms existing methods from the strategic classification literature.

On the Stability of Nonlinear Receding Horizon Control: A Geometric Perspective

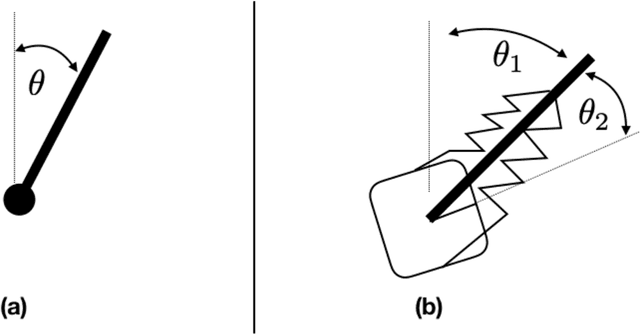
The widespread adoption of nonlinear Receding Horizon Control (RHC) strategies by industry has led to more than 30 years of intense research efforts to provide stability guarantees for these methods. However, current theoretical guarantees require that each (generally nonconvex) planning problem can be solved to (approximate) global optimality, which is an unrealistic requirement for the derivative-based local optimization methods generally used in practical implementations of RHC. This paper takes the first step towards understanding stability guarantees for nonlinear RHC when the inner planning problem is solved to first-order stationary points, but not necessarily global optima. Special attention is given to feedback linearizable systems, and a mixture of positive and negative results are provided. We establish that, under certain strong conditions, first-order solutions to RHC exponentially stabilize linearizable systems. Crucially, this guarantee requires that state costs applied to the planning problems are in a certain sense `compatible' with the global geometry of the system, and a simple counter-example demonstrates the necessity of this condition. These results highlight the need to rethink the role of global geometry in the context of optimization-based control.

Maximum Likelihood Constraint Inference from Stochastic Demonstrations

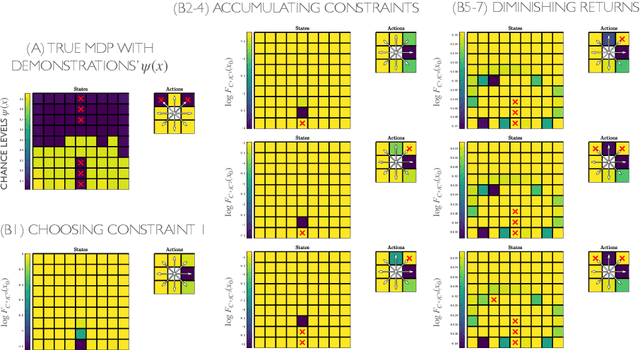
When an expert operates a perilous dynamic system, ideal constraint information is tacitly contained in their demonstrated trajectories and controls. The likelihood of these demonstrations can be computed, given the system dynamics and task objective, and the maximum likelihood constraints can be identified. Prior constraint inference work has focused mainly on deterministic models. Stochastic models, however, can capture the uncertainty and risk tolerance that are often present in real systems of interest. This paper extends maximum likelihood constraint inference to stochastic applications by using maximum causal entropy likelihoods. Furthermore, we propose an efficient algorithm that computes constraint likelihood and risk tolerance in a unified Bellman backup, allowing us to generalize to stochastic systems without increasing computational complexity.

Expert Selection in High-Dimensional Markov Decision Processes

In this work we present a multi-armed bandit framework for online expert selection in Markov decision processes and demonstrate its use in high-dimensional settings. Our method takes a set of candidate expert policies and switches between them to rapidly identify the best performing expert using a variant of the classical upper confidence bound algorithm, thus ensuring low regret in the overall performance of the system. This is useful in applications where several expert policies may be available, and one needs to be selected at run-time for the underlying environment.

Extending DeepSDF for automatic 3D shape retrieval and similarity transform estimation

Recent advances in computer graphics and computer vision have allowed for the development of neural network based generative models for 3D shapes based on signed distance functions (SDFs). These models are useful for shape representation, retrieval and completion. However, this approach to shape retrieval and completion has been limited by the need to have query shapes in the same canonical scale and pose as those observed during training, restricting its effectiveness to real world scenes. In this work, we present a formulation that overcomes this issue by jointly estimating the shape and similarity transformation parameters. We conduct experiments to demonstrate the effectiveness of this formulation on synthetic and real datasets and report favorable comparisons to strong baselines. Finally, we also emphasize the viability of this approach as a form of data compression useful in augmented reality scenarios.