Tijana Zrnic
Look-Ahead Reasoning on Learning Platforms
Nov 18, 2025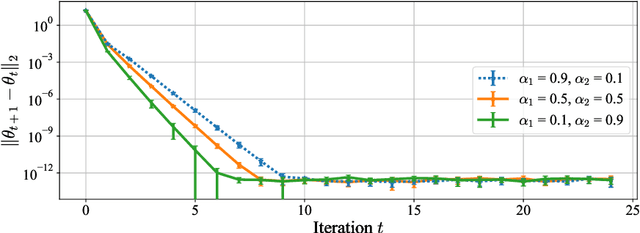
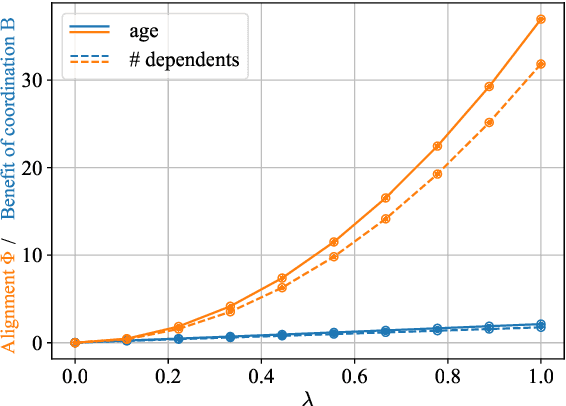
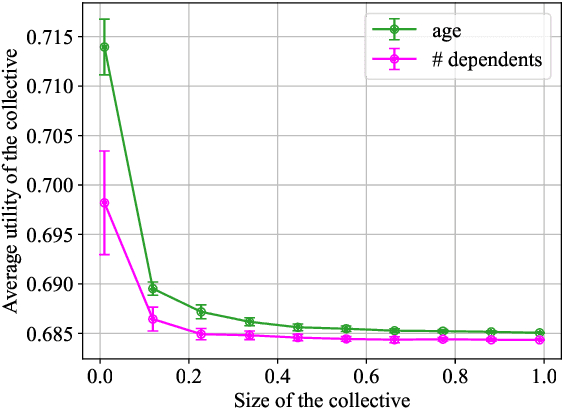
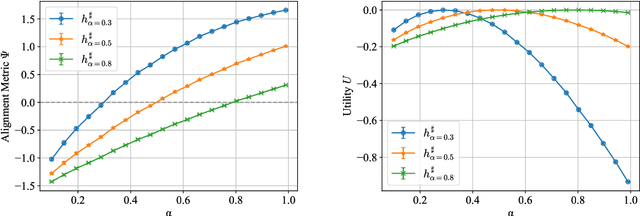
Abstract:On many learning platforms, the optimization criteria guiding model training reflect the priorities of the designer rather than those of the individuals they affect. Consequently, users may act strategically to obtain more favorable outcomes, effectively contesting the platform's predictions. While past work has studied strategic user behavior on learning platforms, the focus has largely been on strategic responses to a deployed model, without considering the behavior of other users. In contrast, look-ahead reasoning takes into account that user actions are coupled, and -- at scale -- impact future predictions. Within this framework, we first formalize level-$k$ thinking, a concept from behavioral economics, where users aim to outsmart their peers by looking one step ahead. We show that, while convergence to an equilibrium is accelerated, the equilibrium remains the same, providing no benefit of higher-level reasoning for individuals in the long run. Then, we focus on collective reasoning, where users take coordinated actions by optimizing through their joint impact on the model. By contrasting collective with selfish behavior, we characterize the benefits and limits of coordination; a new notion of alignment between the learner's and the users' utilities emerges as a key concept. We discuss connections to several related mathematical frameworks, including strategic classification, performative prediction, and algorithmic collective action.
Robust Sampling for Active Statistical Inference
Nov 12, 2025



Abstract:Active statistical inference is a new method for inference with AI-assisted data collection. Given a budget on the number of labeled data points that can be collected and assuming access to an AI predictive model, the basic idea is to improve estimation accuracy by prioritizing the collection of labels where the model is most uncertain. The drawback, however, is that inaccurate uncertainty estimates can make active sampling produce highly noisy results, potentially worse than those from naive uniform sampling. In this work, we present robust sampling strategies for active statistical inference. Robust sampling ensures that the resulting estimator is never worse than the estimator using uniform sampling. Furthermore, with reliable uncertainty estimates, the estimator usually outperforms standard active inference. This is achieved by optimally interpolating between uniform and active sampling, depending on the quality of the uncertainty scores, and by using ideas from robust optimization. We demonstrate the utility of the method on a series of real datasets from computational social science and survey research.
Probably Approximately Correct Labels
Jun 12, 2025



Abstract:Obtaining high-quality labeled datasets is often costly, requiring either extensive human annotation or expensive experiments. We propose a method that supplements such "expert" labels with AI predictions from pre-trained models to construct labeled datasets more cost-effectively. Our approach results in probably approximately correct labels: with high probability, the overall labeling error is small. This solution enables rigorous yet efficient dataset curation using modern AI models. We demonstrate the benefits of the methodology through text annotation with large language models, image labeling with pre-trained vision models, and protein folding analysis with AlphaFold.
Prediction-Powered Inference with Imputed Covariates and Nonuniform Sampling
Jan 30, 2025



Abstract:Machine learning models are increasingly used to produce predictions that serve as input data in subsequent statistical analyses. For example, computer vision predictions of economic and environmental indicators based on satellite imagery are used in downstream regressions; similarly, language models are widely used to approximate human ratings and opinions in social science research. However, failure to properly account for errors in the machine learning predictions renders standard statistical procedures invalid. Prior work uses what we call the Predict-Then-Debias estimator to give valid confidence intervals when machine learning algorithms impute missing variables, assuming a small complete sample from the population of interest. We expand the scope by introducing bootstrap confidence intervals that apply when the complete data is a nonuniform (i.e., weighted, stratified, or clustered) sample and to settings where an arbitrary subset of features is imputed. Importantly, the method can be applied to many settings without requiring additional calculations. We prove that these confidence intervals are valid under no assumptions on the quality of the machine learning model and are no wider than the intervals obtained by methods that do not use machine learning predictions.
Predictions as Surrogates: Revisiting Surrogate Outcomes in the Age of AI
Jan 16, 2025Abstract:We establish a formal connection between the decades-old surrogate outcome model in biostatistics and economics and the emerging field of prediction-powered inference (PPI). The connection treats predictions from pre-trained models, prevalent in the age of AI, as cost-effective surrogates for expensive outcomes. Building on the surrogate outcomes literature, we develop recalibrated prediction-powered inference, a more efficient approach to statistical inference than existing PPI proposals. Our method departs from the existing proposals by using flexible machine learning techniques to learn the optimal ``imputed loss'' through a step we call recalibration. Importantly, the method always improves upon the estimator that relies solely on the data with available true outcomes, even when the optimal imputed loss is estimated imperfectly, and it achieves the smallest asymptotic variance among PPI estimators if the estimate is consistent. Computationally, our optimization objective is convex whenever the loss function that defines the target parameter is convex. We further analyze the benefits of recalibration, both theoretically and numerically, in several common scenarios where machine learning predictions systematically deviate from the outcome of interest. We demonstrate significant gains in effective sample size over existing PPI proposals via three applications leveraging state-of-the-art machine learning/AI models.
A Flexible Defense Against the Winner's Curse
Nov 27, 2024Abstract:Across science and policy, decision-makers often need to draw conclusions about the best candidate among competing alternatives. For instance, researchers may seek to infer the effectiveness of the most successful treatment or determine which demographic group benefits most from a specific treatment. Similarly, in machine learning, practitioners are often interested in the population performance of the model that performs best empirically. However, cherry-picking the best candidate leads to the winner's curse: the observed performance for the winner is biased upwards, rendering conclusions based on standard measures of uncertainty invalid. We introduce the zoom correction, a novel approach for valid inference on the winner. Our method is flexible: it can be employed in both parametric and nonparametric settings, can handle arbitrary dependencies between candidates, and automatically adapts to the level of selection bias. The method easily extends to important related problems, such as inference on the top k winners, inference on the value and identity of the population winner, and inference on "near-winners."
Can Unconfident LLM Annotations Be Used for Confident Conclusions?
Aug 27, 2024Abstract:Large language models (LLMs) have shown high agreement with human raters across a variety of tasks, demonstrating potential to ease the challenges of human data collection. In computational social science (CSS), researchers are increasingly leveraging LLM annotations to complement slow and expensive human annotations. Still, guidelines for collecting and using LLM annotations, without compromising the validity of downstream conclusions, remain limited. We introduce Confidence-Driven Inference: a method that combines LLM annotations and LLM confidence indicators to strategically select which human annotations should be collected, with the goal of producing accurate statistical estimates and provably valid confidence intervals while reducing the number of human annotations needed. Our approach comes with safeguards against LLM annotations of poor quality, guaranteeing that the conclusions will be both valid and no less accurate than if we only relied on human annotations. We demonstrate the effectiveness of Confidence-Driven Inference over baselines in statistical estimation tasks across three CSS settings--text politeness, stance, and bias--reducing the needed number of human annotations by over 25% in each. Although we use CSS settings for demonstration, Confidence-Driven Inference can be used to estimate most standard quantities across a broad range of NLP problems.
A Note on the Prediction-Powered Bootstrap
May 28, 2024



Abstract:We introduce PPBoot: a bootstrap-based method for prediction-powered inference. PPBoot is applicable to arbitrary estimation problems and is very simple to implement, essentially only requiring one application of the bootstrap. Through a series of examples, we demonstrate that PPBoot often performs nearly identically to (and sometimes better than) the earlier PPI(++) method based on asymptotic normality$\unicode{x2013}$when the latter is applicable$\unicode{x2013}$without requiring any asymptotic characterizations. Given its versatility, PPBoot could simplify and expand the scope of application of prediction-powered inference to problems where central limit theorems are hard to prove.
Active Statistical Inference
Mar 05, 2024



Abstract:Inspired by the concept of active learning, we propose active inference$\unicode{x2013}$a methodology for statistical inference with machine-learning-assisted data collection. Assuming a budget on the number of labels that can be collected, the methodology uses a machine learning model to identify which data points would be most beneficial to label, thus effectively utilizing the budget. It operates on a simple yet powerful intuition: prioritize the collection of labels for data points where the model exhibits uncertainty, and rely on the model's predictions where it is confident. Active inference constructs provably valid confidence intervals and hypothesis tests while leveraging any black-box machine learning model and handling any data distribution. The key point is that it achieves the same level of accuracy with far fewer samples than existing baselines relying on non-adaptively-collected data. This means that for the same number of collected samples, active inference enables smaller confidence intervals and more powerful p-values. We evaluate active inference on datasets from public opinion research, census analysis, and proteomics.
PPI++: Efficient Prediction-Powered Inference
Nov 02, 2023Abstract:We present PPI++: a computationally lightweight methodology for estimation and inference based on a small labeled dataset and a typically much larger dataset of machine-learning predictions. The methods automatically adapt to the quality of available predictions, yielding easy-to-compute confidence sets -- for parameters of any dimensionality -- that always improve on classical intervals using only the labeled data. PPI++ builds on prediction-powered inference (PPI), which targets the same problem setting, improving its computational and statistical efficiency. Real and synthetic experiments demonstrate the benefits of the proposed adaptations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge