Rapidly Adapting Policies to the Real World via Simulation-Guided Fine-Tuning

Robot learning requires a considerable amount of high-quality data to realize the promise of generalization. However, large data sets are costly to collect in the real world. Physics simulators can cheaply generate vast data sets with broad coverage over states, actions, and environments. However, physics engines are fundamentally misspecified approximations to reality. This makes direct zero-shot transfer from simulation to reality challenging, especially in tasks where precise and force-sensitive manipulation is necessary. Thus, fine-tuning these policies with small real-world data sets is an appealing pathway for scaling robot learning. However, current reinforcement learning fine-tuning frameworks leverage general, unstructured exploration strategies which are too inefficient to make real-world adaptation practical. This paper introduces the Simulation-Guided Fine-tuning (SGFT) framework, which demonstrates how to extract structural priors from physics simulators to substantially accelerate real-world adaptation. Specifically, our approach uses a value function learned in simulation to guide real-world exploration. We demonstrate this approach across five real-world dexterous manipulation tasks where zero-shot sim-to-real transfer fails. We further demonstrate our framework substantially outperforms baseline fine-tuning methods, requiring up to an order of magnitude fewer real-world samples and succeeding at difficult tasks where prior approaches fail entirely. Last but not least, we provide theoretical justification for this new paradigm which underpins how SGFT can rapidly learn high-performance policies in the face of large sim-to-real dynamics gaps. Project webpage: https://weirdlabuw.github.io/sgft/{weirdlabuw.github.io/sgft}

Dense Dynamics-Aware Reward Synthesis: Integrating Prior Experience with Demonstrations

Many continuous control problems can be formulated as sparse-reward reinforcement learning (RL) tasks. In principle, online RL methods can automatically explore the state space to solve each new task. However, discovering sequences of actions that lead to a non-zero reward becomes exponentially more difficult as the task horizon increases. Manually shaping rewards can accelerate learning for a fixed task, but it is an arduous process that must be repeated for each new environment. We introduce a systematic reward-shaping framework that distills the information contained in 1) a task-agnostic prior data set and 2) a small number of task-specific expert demonstrations, and then uses these priors to synthesize dense dynamics-aware rewards for the given task. This supervision substantially accelerates learning in our experiments, and we provide analysis demonstrating how the approach can effectively guide online learning agents to faraway goals.

Learning to Walk from Three Minutes of Real-World Data with Semi-structured Dynamics Models

Traditionally, model-based reinforcement learning (MBRL) methods exploit neural networks as flexible function approximators to represent a priori unknown environment dynamics. However, training data are typically scarce in practice, and these black-box models often fail to generalize. Modeling architectures that leverage known physics can substantially reduce the complexity of system-identification, but break down in the face of complex phenomena such as contact. We introduce a novel framework for learning semi-structured dynamics models for contact-rich systems which seamlessly integrates structured first principles modeling techniques with black-box auto-regressive models. Specifically, we develop an ensemble of probabilistic models to estimate external forces, conditioned on historical observations and actions, and integrate these predictions using known Lagrangian dynamics. With this semi-structured approach, we can make accurate long-horizon predictions with substantially less data than prior methods. We leverage this capability and propose Semi-Structured Reinforcement Learning (SSRL) a simple model-based learning framework which pushes the sample complexity boundary for real-world learning. We validate our approach on a real-world Unitree Go1 quadruped robot, learning dynamic gaits -- from scratch -- on both hard and soft surfaces with just a few minutes of real-world data. Video and code are available at: https://sites.google.com/utexas.edu/ssrl

Feedback is All You Need: Real-World Reinforcement Learning with Approximate Physics-Based Models

We focus on developing efficient and reliable policy optimization strategies for robot learning with real-world data. In recent years, policy gradient methods have emerged as a promising paradigm for training control policies in simulation. However, these approaches often remain too data inefficient or unreliable to train on real robotic hardware. In this paper we introduce a novel policy gradient-based policy optimization framework which systematically leverages a (possibly highly simplified) first-principles model and enables learning precise control policies with limited amounts of real-world data. Our approach $1)$ uses the derivatives of the model to produce sample-efficient estimates of the policy gradient and $2)$ uses the model to design a low-level tracking controller, which is embedded in the policy class. Theoretical analysis provides insight into how the presence of this feedback controller addresses overcomes key limitations of stand-alone policy gradient methods, while hardware experiments with a small car and quadruped demonstrate that our approach can learn precise control strategies reliably and with only minutes of real-world data.

The Power of Learned Locally Linear Models for Nonlinear Policy Optimization

A common pipeline in learning-based control is to iteratively estimate a model of system dynamics, and apply a trajectory optimization algorithm - e.g.~$\mathtt{iLQR}$ - on the learned model to minimize a target cost. This paper conducts a rigorous analysis of a simplified variant of this strategy for general nonlinear systems. We analyze an algorithm which iterates between estimating local linear models of nonlinear system dynamics and performing $\mathtt{iLQR}$-like policy updates. We demonstrate that this algorithm attains sample complexity polynomial in relevant problem parameters, and, by synthesizing locally stabilizing gains, overcomes exponential dependence in problem horizon. Experimental results validate the performance of our algorithm, and compare to natural deep-learning baselines.

Lyapunov Design for Robust and Efficient Robotic Reinforcement Learning

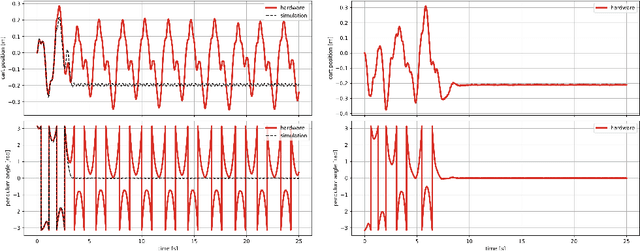
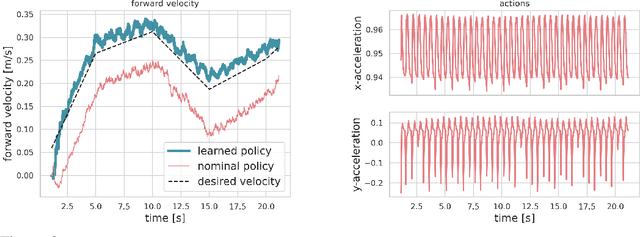
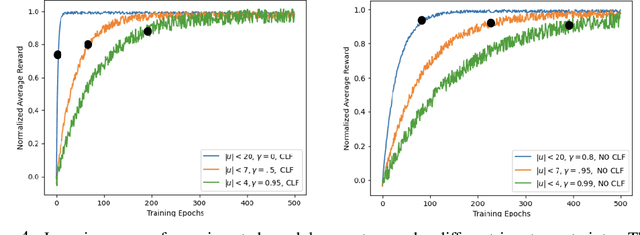
Recent advances in the reinforcement learning (RL) literature have enabled roboticists to automatically train complex policies in simulated environments. However, due to the poor sample complexity of these methods, solving reinforcement learning problems using real-world data remains a challenging problem. This paper introduces a novel cost-shaping method which aims to reduce the number of samples needed to learn a stabilizing controller. The method adds a term involving a control Lyapunov function (CLF) -- an `energy-like' function from the model-based control literature -- to typical cost formulations. Theoretical results demonstrate the new costs lead to stabilizing controllers when smaller discount factors are used, which is well-known to reduce sample complexity. Moreover, the addition of the CLF term `robustifies' the search for a stabilizing controller by ensuring that even highly sub-optimal polices will stabilize the system. We demonstrate our approach with two hardware examples where we learn stabilizing controllers for a cartpole and an A1 quadruped with only seconds and a few minutes of fine-tuning data, respectively.

On the Stability of Nonlinear Receding Horizon Control: A Geometric Perspective

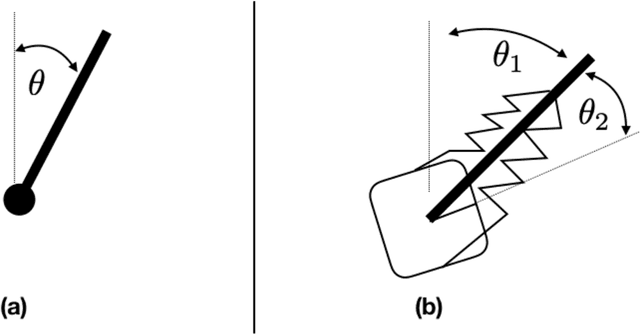
The widespread adoption of nonlinear Receding Horizon Control (RHC) strategies by industry has led to more than 30 years of intense research efforts to provide stability guarantees for these methods. However, current theoretical guarantees require that each (generally nonconvex) planning problem can be solved to (approximate) global optimality, which is an unrealistic requirement for the derivative-based local optimization methods generally used in practical implementations of RHC. This paper takes the first step towards understanding stability guarantees for nonlinear RHC when the inner planning problem is solved to first-order stationary points, but not necessarily global optima. Special attention is given to feedback linearizable systems, and a mixture of positive and negative results are provided. We establish that, under certain strong conditions, first-order solutions to RHC exponentially stabilize linearizable systems. Crucially, this guarantee requires that state costs applied to the planning problems are in a certain sense `compatible' with the global geometry of the system, and a simple counter-example demonstrates the necessity of this condition. These results highlight the need to rethink the role of global geometry in the context of optimization-based control.

Improving Input-Output Linearizing Controllers for Bipedal Robots via Reinforcement Learning

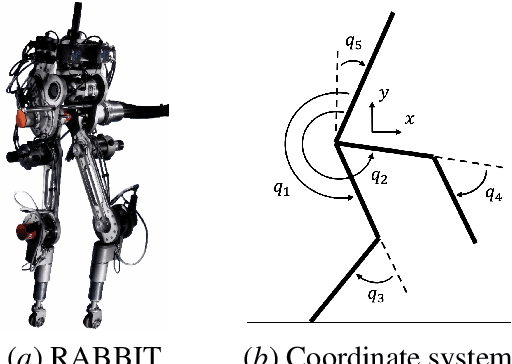
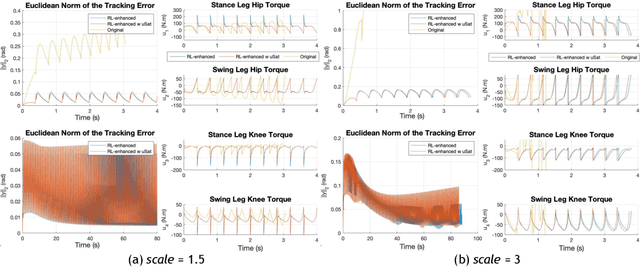
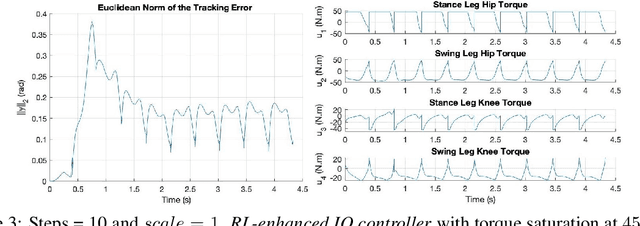
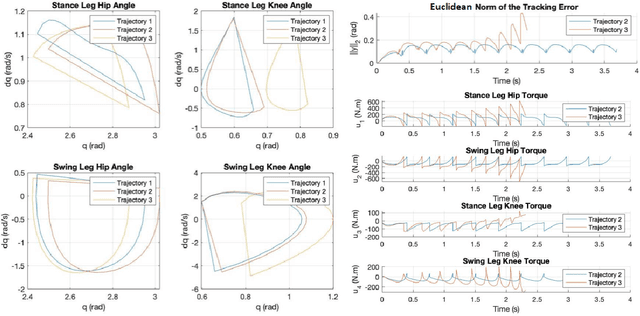
The main drawbacks of input-output linearizing controllers are the need for precise dynamics models and not being able to account for input constraints. Model uncertainty is common in almost every robotic application and input saturation is present in every real world system. In this paper, we address both challenges for the specific case of bipedal robot control by the use of reinforcement learning techniques. Taking the structure of a standard input-output linearizing controller, we use an additive learned term that compensates for model uncertainty. Moreover, by adding constraints to the learning problem we manage to boost the performance of the final controller when input limits are present. We demonstrate the effectiveness of the designed framework for different levels of uncertainty on the five-link planar walking robot RABBIT.

Technical Report: Adaptive Control for Linearizable Systems Using On-Policy Reinforcement Learning

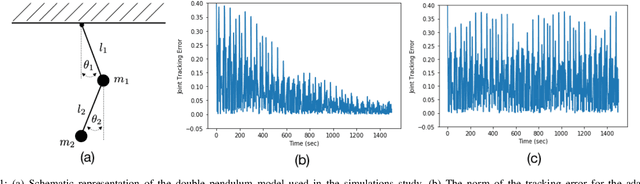
This paper proposes a framework for adaptively learning a feedback linearization-based tracking controller for an unknown system using discrete-time model-free policy-gradient parameter update rules. The primary advantage of the scheme over standard model-reference adaptive control techniques is that it does not require the learned inverse model to be invertible at all instances of time. This enables the use of general function approximators to approximate the linearizing controller for the system without having to worry about singularities. However, the discrete-time and stochastic nature of these algorithms precludes the direct application of standard machinery from the adaptive control literature to provide deterministic stability proofs for the system. Nevertheless, we leverage these techniques alongside tools from the stochastic approximation literature to demonstrate that with high probability the tracking and parameter errors concentrate near zero when a certain persistence of excitation condition is satisfied. A simulated example of a double pendulum demonstrates the utility of the proposed theory. 1

Feedback Linearization for Unknown Systems via Reinforcement Learning

We present a novel approach to control design for nonlinear systems, which leverages reinforcement learning techniques to learn a linearizing controller for a physical plant with unknown dynamics. Feedback linearization is a technique from nonlinear control which renders the input-output dynamics of a nonlinear plant \emph{linear} under application of an appropriate feedback controller. Once a linearizing controller has been constructed, desired output trajectories for the nonlinear plant can be tracked using a variety of linear control techniques. A single learned policy then serves to track arbitrary desired reference signals provided by a higher-level planner. We present theoretical results which provide conditions under which the learning problem has a unique solution which exactly linearizes the plant. We demonstrate the performance of our approach on two simulated problems and a physical robotic platform. For the simulated environments, we observe that the learned feedback linearizing policies can achieve arbitrary tracking of reference trajectories for a fully actuated double pendulum and a 14 dimensional quadrotor. In hardware, we demonstrate that our approach significantly improves tracking performance on a 7-DOF Baxter robot after less than two hours of training.