Reinforcement Learning from User Feedback

As large language models (LLMs) are increasingly deployed in diverse user facing applications, aligning them with real user preferences becomes essential. Existing methods like Reinforcement Learning from Human Feedback (RLHF) rely on expert annotators trained on manually defined guidelines, whose judgments may not reflect the priorities of everyday users. We introduce Reinforcement Learning from User Feedback (RLUF), a framework for aligning LLMs directly to implicit signals from users in production. RLUF addresses key challenges of user feedback: user feedback is often binary (e.g., emoji reactions), sparse, and occasionally adversarial. We train a reward model, P[Love], to predict the likelihood that an LLM response will receive a Love Reaction, a lightweight form of positive user feedback, and integrate P[Love] into a multi-objective policy optimization framework alongside helpfulness and safety objectives. In large-scale experiments, we show that P[Love] is predictive of increased positive feedback and serves as a reliable offline evaluator of future user behavior. Policy optimization using P[Love] significantly raises observed positive-feedback rates, including a 28% increase in Love Reactions during live A/B tests. However, optimizing for positive reactions introduces reward hacking challenges, requiring careful balancing of objectives. By directly leveraging implicit signals from users, RLUF offers a path to aligning LLMs with real-world user preferences at scale.

Learning Auxiliary Tasks Improves Reference-Free Hallucination Detection in Open-Domain Long-Form Generation

Hallucination, the generation of factually incorrect information, remains a significant challenge for large language models (LLMs), especially in open-domain long-form generation. Existing approaches for detecting hallucination in long-form tasks either focus on limited domains or rely heavily on external fact-checking tools, which may not always be available. In this work, we systematically investigate reference-free hallucination detection in open-domain long-form responses. Our findings reveal that internal states (e.g., model's output probability and entropy) alone are insufficient for reliably (i.e., better than random guessing) distinguishing between factual and hallucinated content. To enhance detection, we explore various existing approaches, including prompting-based methods, probing, and fine-tuning, with fine-tuning proving the most effective. To further improve the accuracy, we introduce a new paradigm, named RATE-FT, that augments fine-tuning with an auxiliary task for the model to jointly learn with the main task of hallucination detection. With extensive experiments and analysis using a variety of model families & datasets, we demonstrate the effectiveness and generalizability of our method, e.g., +3% over general fine-tuning methods on LongFact.

Think Smarter not Harder: Adaptive Reasoning with Inference Aware Optimization

Solving mathematics problems has been an intriguing capability of large language models, and many efforts have been made to improve reasoning by extending reasoning length, such as through self-correction and extensive long chain-of-thoughts. While promising in problem-solving, advanced long reasoning chain models exhibit an undesired single-modal behavior, where trivial questions require unnecessarily tedious long chains of thought. In this work, we propose a way to allow models to be aware of inference budgets by formulating it as utility maximization with respect to an inference budget constraint, hence naming our algorithm Inference Budget-Constrained Policy Optimization (IBPO). In a nutshell, models fine-tuned through IBPO learn to ``understand'' the difficulty of queries and allocate inference budgets to harder ones. With different inference budgets, our best models are able to have a $4.14$\% and $5.74$\% absolute improvement ($8.08$\% and $11.2$\% relative improvement) on MATH500 using $2.16$x and $4.32$x inference budgets respectively, relative to LLaMA3.1 8B Instruct. These improvements are approximately $2$x those of self-consistency under the same budgets.

Multi-IF: Benchmarking LLMs on Multi-Turn and Multilingual Instructions Following

Large Language Models (LLMs) have demonstrated impressive capabilities in various tasks, including instruction following, which is crucial for aligning model outputs with user expectations. However, evaluating LLMs' ability to follow instructions remains challenging due to the complexity and subjectivity of human language. Current benchmarks primarily focus on single-turn, monolingual instructions, which do not adequately reflect the complexities of real-world applications that require handling multi-turn and multilingual interactions. To address this gap, we introduce Multi-IF, a new benchmark designed to assess LLMs' proficiency in following multi-turn and multilingual instructions. Multi-IF, which utilizes a hybrid framework combining LLM and human annotators, expands upon the IFEval by incorporating multi-turn sequences and translating the English prompts into another 7 languages, resulting in a dataset of 4,501 multilingual conversations, where each has three turns. Our evaluation of 14 state-of-the-art LLMs on Multi-IF reveals that it presents a significantly more challenging task than existing benchmarks. All the models tested showed a higher rate of failure in executing instructions correctly with each additional turn. For example, o1-preview drops from 0.877 at the first turn to 0.707 at the third turn in terms of average accuracy over all languages. Moreover, languages with non-Latin scripts (Hindi, Russian, and Chinese) generally exhibit higher error rates, suggesting potential limitations in the models' multilingual capabilities. We release Multi-IF prompts and the evaluation code base to encourage further research in this critical area.

Preference Optimization with Multi-Sample Comparisons

Recent advancements in generative models, particularly large language models (LLMs) and diffusion models, have been driven by extensive pretraining on large datasets followed by post-training. However, current post-training methods such as reinforcement learning from human feedback (RLHF) and direct alignment from preference methods (DAP) primarily utilize single-sample comparisons. These approaches often fail to capture critical characteristics such as generative diversity and bias, which are more accurately assessed through multiple samples. To address these limitations, we introduce a novel approach that extends post-training to include multi-sample comparisons. To achieve this, we propose Multi-sample Direct Preference Optimization (mDPO) and Multi-sample Identity Preference Optimization (mIPO). These methods improve traditional DAP methods by focusing on group-wise characteristics. Empirically, we demonstrate that multi-sample comparison is more effective in optimizing collective characteristics~(e.g., diversity and bias) for generative models than single-sample comparison. Additionally, our findings suggest that multi-sample comparisons provide a more robust optimization framework, particularly for dataset with label noise.

The Perfect Blend: Redefining RLHF with Mixture of Judges

Reinforcement learning from human feedback (RLHF) has become the leading approach for fine-tuning large language models (LLM). However, RLHF has limitations in multi-task learning (MTL) due to challenges of reward hacking and extreme multi-objective optimization (i.e., trade-off of multiple and/or sometimes conflicting objectives). Applying RLHF for MTL currently requires careful tuning of the weights for reward model and data combinations. This is often done via human intuition and does not generalize. In this work, we introduce a novel post-training paradigm which we called Constrained Generative Policy Optimization (CGPO). The core of CGPO is Mixture of Judges (MoJ) with cost-efficient constrained policy optimization with stratification, which can identify the perfect blend in RLHF in a principled manner. It shows strong empirical results with theoretical guarantees, does not require extensive hyper-parameter tuning, and is plug-and-play in common post-training pipelines. Together, this can detect and mitigate reward hacking behaviors while reaching a pareto-optimal point across an extremely large number of objectives. Our empirical evaluations demonstrate that CGPO significantly outperforms standard RLHF algorithms like PPO and DPO across various tasks including general chat, STEM questions, instruction following, and coding. Specifically, CGPO shows improvements of 7.4% in AlpacaEval-2 (general chat), 12.5% in Arena-Hard (STEM & reasoning), and consistent gains in other domains like math and coding. Notably, PPO, while commonly used, is prone to severe reward hacking in popular coding benchmarks, which CGPO successfully addresses. This breakthrough in RLHF not only tackles reward hacking and extreme multi-objective optimization challenges but also advances the state-of-the-art in aligning general-purpose LLMs for diverse applications.

On the Equivalence of Graph Convolution and Mixup

This paper investigates the relationship between graph convolution and Mixup techniques. Graph convolution in a graph neural network involves aggregating features from neighboring samples to learn representative features for a specific node or sample. On the other hand, Mixup is a data augmentation technique that generates new examples by averaging features and one-hot labels from multiple samples. One commonality between these techniques is their utilization of information from multiple samples to derive feature representation. This study aims to explore whether a connection exists between these two approaches. Our investigation reveals that, under two mild conditions, graph convolution can be viewed as a specialized form of Mixup that is applied during both the training and testing phases. The two conditions are: 1) \textit{Homophily Relabel} - assigning the target node's label to all its neighbors, and 2) \textit{Test-Time Mixup} - Mixup the feature during the test time. We establish this equivalence mathematically by demonstrating that graph convolution networks (GCN) and simplified graph convolution (SGC) can be expressed as a form of Mixup. We also empirically verify the equivalence by training an MLP using the two conditions to achieve comparable performance.

Effective Long-Context Scaling of Foundation Models

We present a series of long-context LLMs that support effective context windows of up to 32,768 tokens. Our model series are built through continual pretraining from Llama 2 with longer training sequences and on a dataset where long texts are upsampled. We perform extensive evaluation on language modeling, synthetic context probing tasks, and a wide range of research benchmarks. On research benchmarks, our models achieve consistent improvements on most regular tasks and significant improvements on long-context tasks over Llama 2. Notably, with a cost-effective instruction tuning procedure that does not require human-annotated long instruction data, the 70B variant can already surpass gpt-3.5-turbo-16k's overall performance on a suite of long-context tasks. Alongside these results, we provide an in-depth analysis on the individual components of our method. We delve into Llama's position encodings and discuss its limitation in modeling long dependencies. We also examine the impact of various design choices in the pretraining process, including the data mix and the training curriculum of sequence lengths -- our ablation experiments suggest that having abundant long texts in the pretrain dataset is not the key to achieving strong performance, and we empirically verify that long context continual pretraining is more efficient and similarly effective compared to pretraining from scratch with long sequences.

BayesFormer: Transformer with Uncertainty Estimation

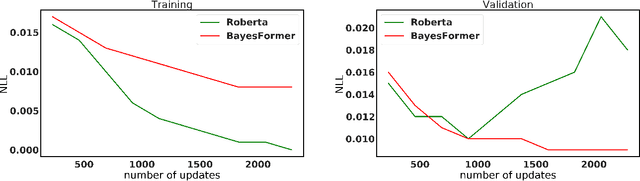
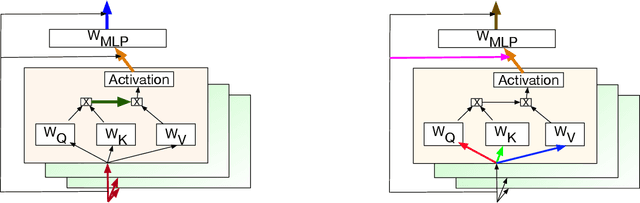
Transformer has become ubiquitous due to its dominant performance in various NLP and image processing tasks. However, it lacks understanding of how to generate mathematically grounded uncertainty estimates for transformer architectures. Models equipped with such uncertainty estimates can typically improve predictive performance, make networks robust, avoid over-fitting and used as acquisition function in active learning. In this paper, we introduce BayesFormer, a Transformer model with dropouts designed by Bayesian theory. We proposed a new theoretical framework to extend the approximate variational inference-based dropout to Transformer-based architectures. Through extensive experiments, we validate the proposed architecture in four paradigms and show improvements across the board: language modeling and classification, long-sequence understanding, machine translation and acquisition function for active learning.

Stochastic Bandits for Multi-platform Budget Optimization in Online Advertising

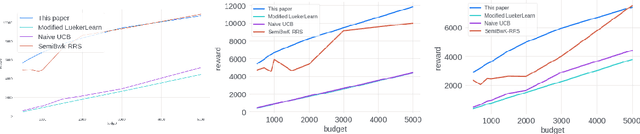
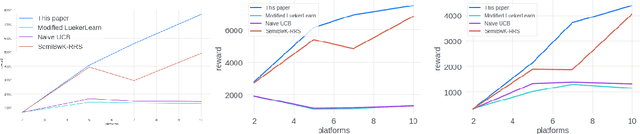
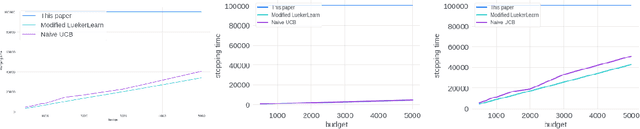
We study the problem of an online advertising system that wants to optimally spend an advertiser's given budget for a campaign across multiple platforms, without knowing the value for showing an ad to the users on those platforms. We model this challenging practical application as a Stochastic Bandits with Knapsacks problem over $T$ rounds of bidding with the set of arms given by the set of distinct bidding $m$-tuples, where $m$ is the number of platforms. We modify the algorithm proposed in Badanidiyuru \emph{et al.,} to extend it to the case of multiple platforms to obtain an algorithm for both the discrete and continuous bid-spaces. Namely, for discrete bid spaces we give an algorithm with regret $O\left(OPT \sqrt {\frac{mn}{B} }+ \sqrt{mn OPT}\right)$, where $OPT$ is the performance of the optimal algorithm that knows the distributions. For continuous bid spaces the regret of our algorithm is $\tilde{O}\left(m^{1/3} \cdot \min\left\{ B^{2/3}, (m T)^{2/3} \right\} \right)$. When restricted to this special-case, this bound improves over Sankararaman and Slivkins in the regime $OPT \ll T$, as is the case in the particular application at hand. Second, we show an $ \Omega\left (\sqrt {m OPT} \right)$ lower bound for the discrete case and an $\Omega\left( m^{1/3} B^{2/3}\right)$ lower bound for the continuous setting, almost matching the upper bounds. Finally, we use a real-world data set from a large internet online advertising company with multiple ad platforms and show that our algorithms outperform common benchmarks and satisfy the required properties warranted in the real-world application.