Detecting Bias and Enhancing Diagnostic Accuracy in Large Language Models for Healthcare

Biased AI-generated medical advice and misdiagnoses can jeopardize patient safety, making the integrity of AI in healthcare more critical than ever. As Large Language Models (LLMs) take on a growing role in medical decision-making, addressing their biases and enhancing their accuracy is key to delivering safe, reliable care. This study addresses these challenges head-on by introducing new resources designed to promote ethical and precise AI in healthcare. We present two datasets: BiasMD, featuring 6,007 question-answer pairs crafted to evaluate and mitigate biases in health-related LLM outputs, and DiseaseMatcher, with 32,000 clinical question-answer pairs spanning 700 diseases, aimed at assessing symptom-based diagnostic accuracy. Using these datasets, we developed the EthiClinician, a fine-tuned model built on the ChatDoctor framework, which outperforms GPT-4 in both ethical reasoning and clinical judgment. By exposing and correcting hidden biases in existing models for healthcare, our work sets a new benchmark for safer, more reliable patient outcomes.

Resprompt: Residual Connection Prompting Advances Multi-Step Reasoning in Large Language Models

Chain-of-thought (CoT) prompting, which offers step-by-step problem-solving rationales, has impressively unlocked the reasoning potential of large language models (LLMs). Yet, the standard CoT is less effective in problems demanding multiple reasoning steps. This limitation arises from the complex reasoning process in multi-step problems: later stages often depend on the results of several steps earlier, not just the results of the immediately preceding step. Such complexities suggest the reasoning process is naturally represented as a graph. The almost linear and straightforward structure of CoT prompting, however, struggles to capture this complex reasoning graph. To address this challenge, we propose Residual Connection Prompting (RESPROMPT), a new prompting strategy that advances multi-step reasoning in LLMs. Our key idea is to reconstruct the reasoning graph within prompts. We achieve this by integrating necessary connections-links present in the reasoning graph but missing in the linear CoT flow-into the prompts. Termed "residual connections", these links are pivotal in morphing the linear CoT structure into a graph representation, effectively capturing the complex reasoning graphs inherent in multi-step problems. We evaluate RESPROMPT on six benchmarks across three diverse domains: math, sequential, and commonsense reasoning. For the open-sourced LLaMA family of models, RESPROMPT yields a significant average reasoning accuracy improvement of 12.5% on LLaMA-65B and 6.8% on LLaMA2-70B. Breakdown analysis further highlights RESPROMPT particularly excels in complex multi-step reasoning: for questions demanding at least five reasoning steps, RESPROMPT outperforms the best CoT based benchmarks by a remarkable average improvement of 21.1% on LLaMA-65B and 14.3% on LLaMA2-70B. Through extensive ablation studies and analyses, we pinpoint how to most effectively build residual connections.

On the Equivalence of Graph Convolution and Mixup

This paper investigates the relationship between graph convolution and Mixup techniques. Graph convolution in a graph neural network involves aggregating features from neighboring samples to learn representative features for a specific node or sample. On the other hand, Mixup is a data augmentation technique that generates new examples by averaging features and one-hot labels from multiple samples. One commonality between these techniques is their utilization of information from multiple samples to derive feature representation. This study aims to explore whether a connection exists between these two approaches. Our investigation reveals that, under two mild conditions, graph convolution can be viewed as a specialized form of Mixup that is applied during both the training and testing phases. The two conditions are: 1) \textit{Homophily Relabel} - assigning the target node's label to all its neighbors, and 2) \textit{Test-Time Mixup} - Mixup the feature during the test time. We establish this equivalence mathematically by demonstrating that graph convolution networks (GCN) and simplified graph convolution (SGC) can be expressed as a form of Mixup. We also empirically verify the equivalence by training an MLP using the two conditions to achieve comparable performance.

Prosody Transfer in Neural Text to Speech Using Global Pitch and Loudness Features

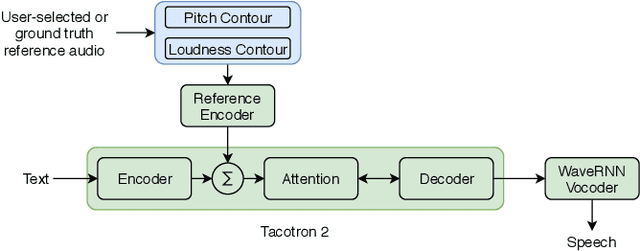
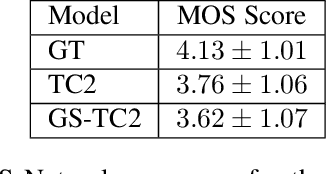
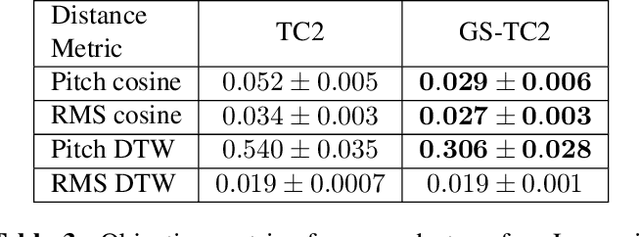
This paper presents a simple yet effective method to achieve prosody transfer from a reference speech signal to synthesized speech. The main idea is to incorporate well-known acoustic correlates of prosody such as pitch and loudness contours of the reference speech into a modern neural text-to-speech (TTS) synthesizer such as Tacotron2 (TC2). More specifically, a small set of acoustic features are extracted from the reference audio and then used to condition a TC2 synthesizer. The trained model is evaluated using subjective listening tests and novel objective evaluations of prosody transfer are proposed. Listening tests show that the synthesized speech is rated as highly natural and that prosody is successfully transferred from the reference speech signal to the synthesized signal.

Learning Mixtures of Separable Dictionaries for Tensor Data: Analysis and Algorithms

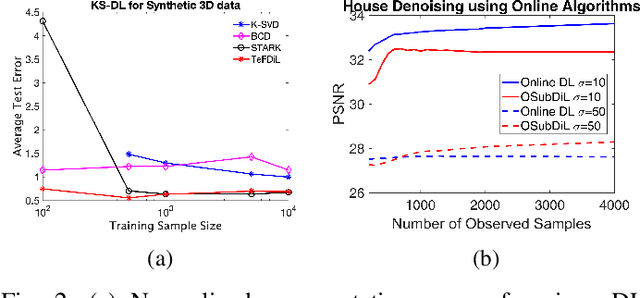
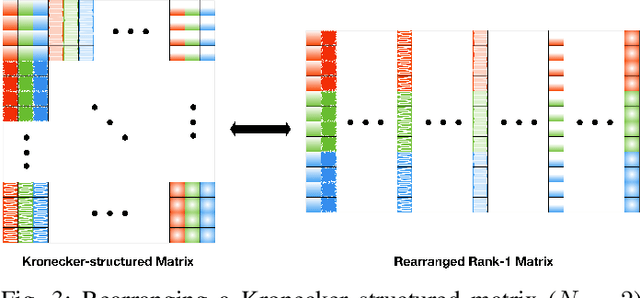
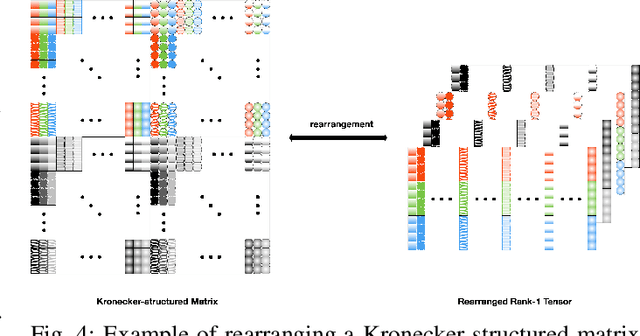
This work addresses the problem of learning sparse representations of tensor data using structured dictionary learning. It proposes learning a mixture of separable dictionaries to better capture the structure of tensor data by generalizing the separable dictionary learning model. Two different approaches for learning mixture of separable dictionaries are explored and sufficient conditions for local identifiability of the underlying dictionary are derived in each case. Moreover, computational algorithms are developed to solve the problem of learning mixture of separable dictionaries in both batch and online settings. Numerical experiments are used to show the usefulness of the proposed model and the efficacy of the developed algorithms.

Identifiability of Kronecker-structured Dictionaries for Tensor Data

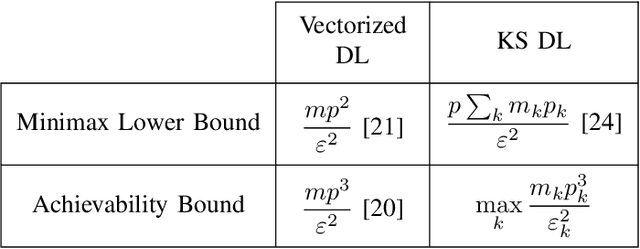
This paper derives sufficient conditions for local recovery of coordinate dictionaries comprising a Kronecker-structured dictionary that is used for representing $K$th-order tensor data. Tensor observations are assumed to be generated from a Kronecker-structured dictionary multiplied by sparse coefficient tensors that follow the separable sparsity model. This work provides sufficient conditions on the underlying coordinate dictionaries, coefficient and noise distributions, and number of samples that guarantee recovery of the individual coordinate dictionaries up to a specified error, as a local minimum of the objective function, with high probability. In particular, the sample complexity to recover $K$ coordinate dictionaries with dimensions $m_k \times p_k$ up to estimation error $\varepsilon_k$ is shown to be $\max_{k \in [K]}\mathcal{O}(m_kp_k^3\varepsilon_k^{-2})$.

STARK: Structured Dictionary Learning Through Rank-one Tensor Recovery

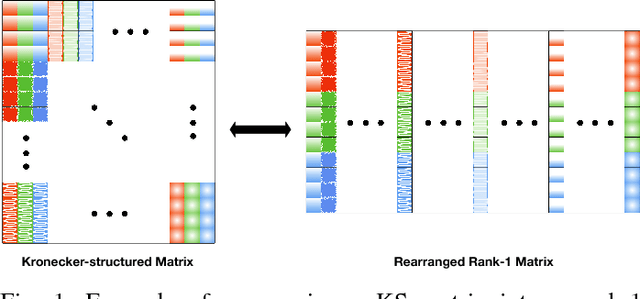
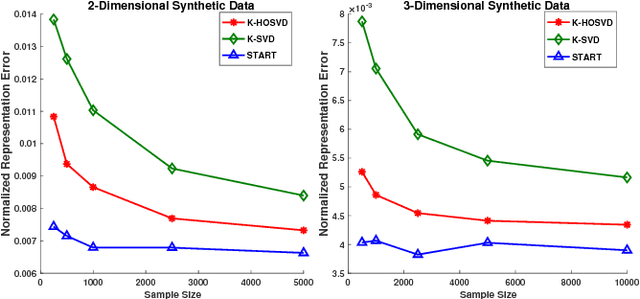
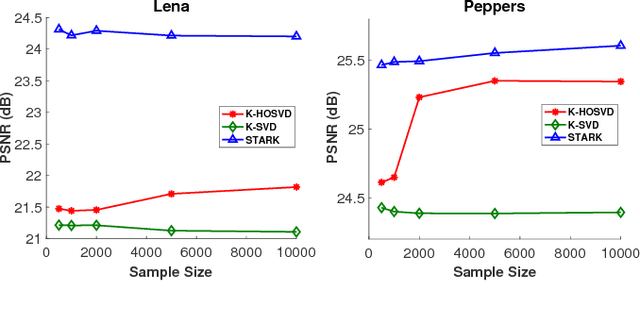
In recent years, a class of dictionaries have been proposed for multidimensional (tensor) data representation that exploit the structure of tensor data by imposing a Kronecker structure on the dictionary underlying the data. In this work, a novel algorithm called "STARK" is provided to learn Kronecker structured dictionaries that can represent tensors of any order. By establishing that the Kronecker product of any number of matrices can be rearranged to form a rank-1 tensor, we show that Kronecker structure can be enforced on the dictionary by solving a rank-1 tensor recovery problem. Because rank-1 tensor recovery is a challenging nonconvex problem, we resort to solving a convex relaxation of this problem. Empirical experiments on synthetic and real data show promising results for our proposed algorithm.

Minimax Lower Bounds for Kronecker-Structured Dictionary Learning

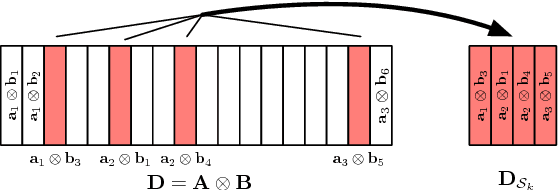
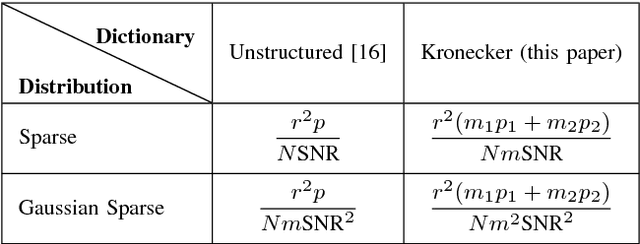
Dictionary learning is the problem of estimating the collection of atomic elements that provide a sparse representation of measured/collected signals or data. This paper finds fundamental limits on the sample complexity of estimating dictionaries for tensor data by proving a lower bound on the minimax risk. This lower bound depends on the dimensions of the tensor and parameters of the generative model. The focus of this paper is on second-order tensor data, with the underlying dictionaries constructed by taking the Kronecker product of two smaller dictionaries and the observed data generated by sparse linear combinations of dictionary atoms observed through white Gaussian noise. In this regard, the paper provides a general lower bound on the minimax risk and also adapts the proof techniques for equivalent results using sparse and Gaussian coefficient models. The reported results suggest that the sample complexity of dictionary learning for tensor data can be significantly lower than that for unstructured data.