Boosting LLM Reasoning via Spontaneous Self-Correction

While large language models (LLMs) have demonstrated remarkable success on a broad range of tasks, math reasoning remains a challenging one. One of the approaches for improving math reasoning is self-correction, which designs self-improving loops to let the model correct its own mistakes. However, existing self-correction approaches treat corrections as standalone post-generation refinements, relying on extra prompt and system designs to elicit self-corrections, instead of performing real-time, spontaneous self-corrections in a single pass. To address this, we propose SPOC, a spontaneous self-correction approach that enables LLMs to generate interleaved solutions and verifications in a single inference pass, with generation dynamically terminated based on verification outcomes, thereby effectively scaling inference time compute. SPOC considers a multi-agent perspective by assigning dual roles -- solution proposer and verifier -- to the same model. We adopt a simple yet effective approach to generate synthetic data for fine-tuning, enabling the model to develop capabilities for self-verification and multi-agent collaboration. We further improve its solution proposal and verification accuracy through online reinforcement learning. Experiments on mathematical reasoning benchmarks show that SPOC significantly improves performance. Notably, SPOC boosts the accuracy of Llama-3.1-8B and 70B Instruct models, achieving gains of 8.8% and 11.6% on MATH500, 10.0% and 20.0% on AMC23, and 3.3% and 6.7% on AIME24, respectively.

Language Model Distillation: A Temporal Difference Imitation Learning Perspective

Large language models have led to significant progress across many NLP tasks, although their massive sizes often incur substantial computational costs. Distillation has become a common practice to compress these large and highly capable models into smaller, more efficient ones. Many existing language model distillation methods can be viewed as behavior cloning from the perspective of imitation learning or inverse reinforcement learning. This viewpoint has inspired subsequent studies that leverage (inverse) reinforcement learning techniques, including variations of behavior cloning and temporal difference learning methods. Rather than proposing yet another specific temporal difference method, we introduce a general framework for temporal difference-based distillation by exploiting the distributional sparsity of the teacher model. Specifically, it is often observed that language models assign most probability mass to a small subset of tokens. Motivated by this observation, we design a temporal difference learning framework that operates on a reduced action space (a subset of vocabulary), and demonstrate how practical algorithms can be derived and the resulting performance improvements.

Think Smarter not Harder: Adaptive Reasoning with Inference Aware Optimization

Solving mathematics problems has been an intriguing capability of large language models, and many efforts have been made to improve reasoning by extending reasoning length, such as through self-correction and extensive long chain-of-thoughts. While promising in problem-solving, advanced long reasoning chain models exhibit an undesired single-modal behavior, where trivial questions require unnecessarily tedious long chains of thought. In this work, we propose a way to allow models to be aware of inference budgets by formulating it as utility maximization with respect to an inference budget constraint, hence naming our algorithm Inference Budget-Constrained Policy Optimization (IBPO). In a nutshell, models fine-tuned through IBPO learn to ``understand'' the difficulty of queries and allocate inference budgets to harder ones. With different inference budgets, our best models are able to have a $4.14$\% and $5.74$\% absolute improvement ($8.08$\% and $11.2$\% relative improvement) on MATH500 using $2.16$x and $4.32$x inference budgets respectively, relative to LLaMA3.1 8B Instruct. These improvements are approximately $2$x those of self-consistency under the same budgets.

$\mathcal{B}$-Coder: Value-Based Deep Reinforcement Learning for Program Synthesis

Program synthesis aims to create accurate, executable code from natural language descriptions. This field has leveraged the power of reinforcement learning (RL) in conjunction with large language models (LLMs), significantly enhancing code generation capabilities. This integration focuses on directly optimizing functional correctness, transcending conventional supervised losses. While current literature predominantly favors policy-based algorithms, attributes of program synthesis suggest a natural compatibility with value-based methods. This stems from rich collection of off-policy programs developed by human programmers, and the straightforward verification of generated programs through automated unit testing (i.e. easily obtainable rewards in RL language). Diverging from the predominant use of policy-based algorithms, our work explores the applicability of value-based approaches, leading to the development of our $\mathcal{B}$-Coder (pronounced Bellman coder). Yet, training value-based methods presents challenges due to the enormous search space inherent to program synthesis. To this end, we propose an initialization protocol for RL agents utilizing pre-trained LMs and a conservative Bellman operator to reduce training complexities. Moreover, we demonstrate how to leverage the learned value functions as a dual strategy to post-process generated programs. Our empirical evaluations demonstrated $\mathcal{B}$-Coder's capability in achieving state-of-the-art performance compared with policy-based methods. Remarkably, this achievement is reached with minimal reward engineering effort, highlighting the effectiveness of value-based RL, independent of reward designs.

Slowly Changing Adversarial Bandit Algorithms are Provably Efficient for Discounted MDPs

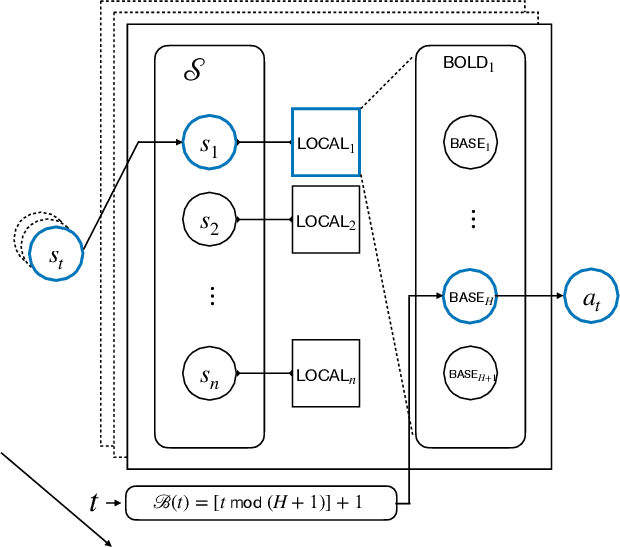
Reinforcement learning (RL) generalizes bandit problems with additional difficulties on longer planning horzion and unknown transition kernel. We show that, under some mild assumptions, \textbf{any} slowly changing adversarial bandit algorithm enjoys near-optimal regret in adversarial bandits can achieve near-optimal (expected) regret in non-episodic discounted MDPs. The slowly changing property required by our generalization is mild, see e.g. (Even-Dar et al. 2009, Neu et al. 2010), we also show, for example, \expt~(Auer et al. 2002) is slowly changing and enjoys near-optimal regret in MDPs.

Orthogonal Gromov-Wasserstein Discrepancy with Efficient Lower Bound

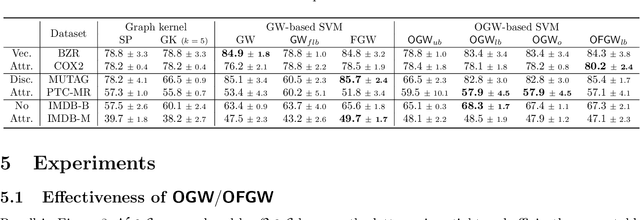
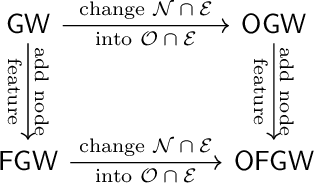
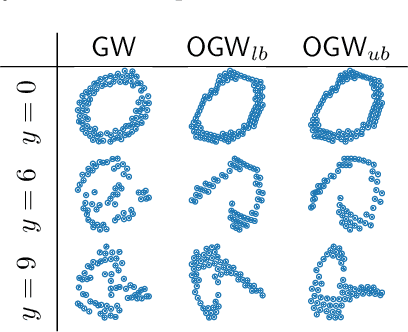
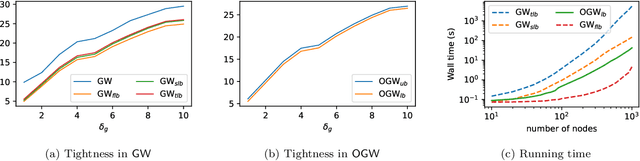
Comparing structured data from possibly different metric-measure spaces is a fundamental task in machine learning, with applications in, e.g., graph classification. The Gromov-Wasserstein (GW) discrepancy formulates a coupling between the structured data based on optimal transportation, tackling the incomparability between different structures by aligning the intra-relational geometries. Although efficient local solvers such as conditional gradient and Sinkhorn are available, the inherent non-convexity still prevents a tractable evaluation, and the existing lower bounds are not tight enough for practical use. To address this issue, we take inspiration from the connection with the quadratic assignment problem, and propose the orthogonal Gromov-Wasserstein (OGW) discrepancy as a surrogate of GW. It admits an efficient and closed-form lower bound with the complexity of $\mathcal{O}(n^3)$, and directly extends to the fused Gromov-Wasserstein (FGW) distance, incorporating node features into the coupling. Extensive experiments on both the synthetic and real-world datasets show the tightness of our lower bounds, and both OGW and its lower bounds efficiently deliver accurate predictions and satisfactory barycenters for graph sets.