TransMPC: Transformer-based Explicit MPC with Variable Prediction Horizon

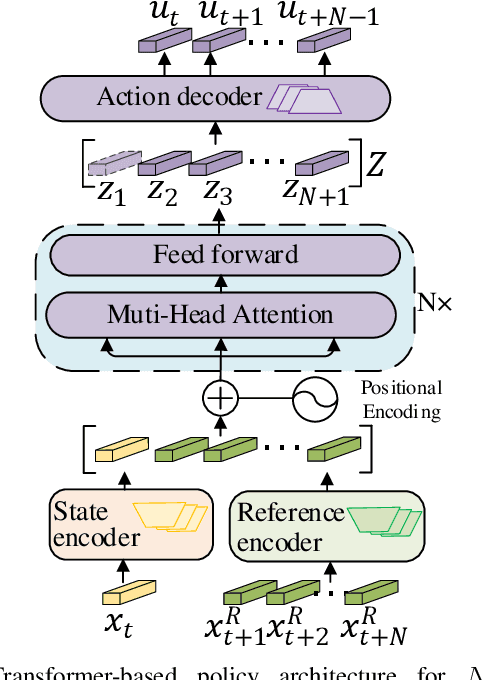
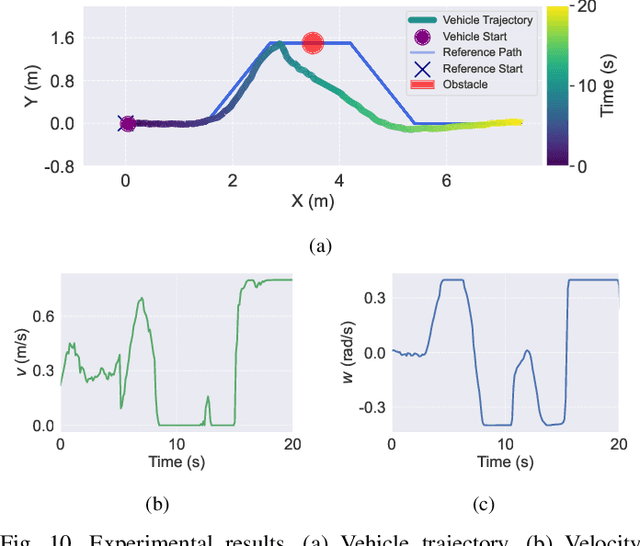
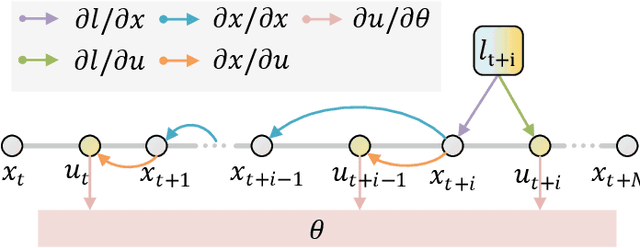
Traditional online Model Predictive Control (MPC) methods often suffer from excessive computational complexity, limiting their practical deployment. Explicit MPC mitigates online computational load by pre-computing control policies offline; however, existing explicit MPC methods typically rely on simplified system dynamics and cost functions, restricting their accuracy for complex systems. This paper proposes TransMPC, a novel Transformer-based explicit MPC algorithm capable of generating highly accurate control sequences in real-time for complex dynamic systems. Specifically, we formulate the MPC policy as an encoder-only Transformer leveraging bidirectional self-attention, enabling simultaneous inference of entire control sequences in a single forward pass. This design inherently accommodates variable prediction horizons while ensuring low inference latency. Furthermore, we introduce a direct policy optimization framework that alternates between sampling and learning phases. Unlike imitation-based approaches dependent on precomputed optimal trajectories, TransMPC directly optimizes the true finite-horizon cost via automatic differentiation. Random horizon sampling combined with a replay buffer provides independent and identically distributed (i.i.d.) training samples, ensuring robust generalization across varying states and horizon lengths. Extensive simulations and real-world vehicle control experiments validate the effectiveness of TransMPC in terms of solution accuracy, adaptability to varying horizons, and computational efficiency.

Distributional Soft Actor-Critic with Diffusion Policy

Reinforcement learning has been proven to be highly effective in handling complex control tasks. Traditional methods typically use unimodal distributions, such as Gaussian distributions, to model the output of value distributions. However, unimodal distribution often and easily causes bias in value function estimation, leading to poor algorithm performance. This paper proposes a distributional reinforcement learning algorithm called DSAC-D (Distributed Soft Actor Critic with Diffusion Policy) to address the challenges of estimating bias in value functions and obtaining multimodal policy representations. A multimodal distributional policy iteration framework that can converge to the optimal policy was established by introducing policy entropy and value distribution function. A diffusion value network that can accurately characterize the distribution of multi peaks was constructed by generating a set of reward samples through reverse sampling using a diffusion model. Based on this, a distributional reinforcement learning algorithm with dual diffusion of the value network and the policy network was derived. MuJoCo testing tasks demonstrate that the proposed algorithm not only learns multimodal policy, but also achieves state-of-the-art (SOTA) performance in all 9 control tasks, with significant suppression of estimation bias and total average return improvement of over 10\% compared to existing mainstream algorithms. The results of real vehicle testing show that DSAC-D can accurately characterize the multimodal distribution of different driving styles, and the diffusion policy network can characterize multimodal trajectories.

Enhanced DACER Algorithm with High Diffusion Efficiency

Due to their expressive capacity, diffusion models have shown great promise in offline RL and imitation learning. Diffusion Actor-Critic with Entropy Regulator (DACER) extended this capability to online RL by using the reverse diffusion process as a policy approximator, trained end-to-end with policy gradient methods, achieving strong performance. However, this comes at the cost of requiring many diffusion steps, which significantly hampers training efficiency, while directly reducing the steps leads to noticeable performance degradation. Critically, the lack of inference efficiency becomes a significant bottleneck for applying diffusion policies in real-time online RL settings. To improve training and inference efficiency while maintaining or even enhancing performance, we propose a Q-gradient field objective as an auxiliary optimization target to guide the denoising process at each diffusion step. Nonetheless, we observe that the independence of the Q-gradient field from the diffusion time step negatively impacts the performance of the diffusion policy. To address this, we introduce a temporal weighting mechanism that enables the model to efficiently eliminate large-scale noise in the early stages and refine actions in the later stages. Experimental results on MuJoCo benchmarks and several multimodal tasks demonstrate that the DACER2 algorithm achieves state-of-the-art performance in most MuJoCo control tasks with only five diffusion steps, while also exhibiting stronger multimodality compared to DACER.

Global Optimality of Single-Timescale Actor-Critic under Continuous State-Action Space: A Study on Linear Quadratic Regulator

Actor-critic methods have achieved state-of-the-art performance in various challenging tasks. However, theoretical understandings of their performance remain elusive and challenging. Existing studies mostly focus on practically uncommon variants such as double-loop or two-timescale stepsize actor-critic algorithms for simplicity. These results certify local convergence on finite state- or action-space only. We push the boundary to investigate the classic single-sample single-timescale actor-critic on continuous (infinite) state-action space, where we employ the canonical linear quadratic regulator (LQR) problem as a case study. We show that the popular single-timescale actor-critic can attain an epsilon-optimal solution with an order of epsilon to -2 sample complexity for solving LQR on the demanding continuous state-action space. Our work provides new insights into the performance of single-timescale actor-critic, which further bridges the gap between theory and practice.

Predictive Lagrangian Optimization for Constrained Reinforcement Learning

Constrained optimization is popularly seen in reinforcement learning for addressing complex control tasks. From the perspective of dynamic system, iteratively solving a constrained optimization problem can be framed as the temporal evolution of a feedback control system. Classical constrained optimization methods, such as penalty and Lagrangian approaches, inherently use proportional and integral feedback controllers. In this paper, we propose a more generic equivalence framework to build the connection between constrained optimization and feedback control system, for the purpose of developing more effective constrained RL algorithms. Firstly, we define that each step of the system evolution determines the Lagrange multiplier by solving a multiplier feedback optimal control problem (MFOCP). In this problem, the control input is multiplier, the state is policy parameters, the dynamics is described by policy gradient descent, and the objective is to minimize constraint violations. Then, we introduce a multiplier guided policy learning (MGPL) module to perform policy parameters updating. And we prove that the resulting optimal policy, achieved through alternating MFOCP and MGPL, aligns with the solution of the primal constrained RL problem, thereby establishing our equivalence framework. Furthermore, we point out that the existing PID Lagrangian is merely one special case within our framework that utilizes a PID controller. We also accommodate the integration of other various feedback controllers, thereby facilitating the development of new algorithms. As a representative, we employ model predictive control (MPC) as the feedback controller and consequently propose a new algorithm called predictive Lagrangian optimization (PLO). Numerical experiments demonstrate its superiority over the PID Lagrangian method, achieving a larger feasible region up to 7.2% and a comparable average reward.

Conformal Symplectic Optimization for Stable Reinforcement Learning

Training deep reinforcement learning (RL) agents necessitates overcoming the highly unstable nonconvex stochastic optimization inherent in the trial-and-error mechanism. To tackle this challenge, we propose a physics-inspired optimization algorithm called relativistic adaptive gradient descent (RAD), which enhances long-term training stability. By conceptualizing neural network (NN) training as the evolution of a conformal Hamiltonian system, we present a universal framework for transferring long-term stability from conformal symplectic integrators to iterative NN updating rules, where the choice of kinetic energy governs the dynamical properties of resulting optimization algorithms. By utilizing relativistic kinetic energy, RAD incorporates principles from special relativity and limits parameter updates below a finite speed, effectively mitigating abnormal gradient influences. Additionally, RAD models NN optimization as the evolution of a multi-particle system where each trainable parameter acts as an independent particle with an individual adaptive learning rate. We prove RAD's sublinear convergence under general nonconvex settings, where smaller gradient variance and larger batch sizes contribute to tighter convergence. Notably, RAD degrades to the well-known adaptive moment estimation (ADAM) algorithm when its speed coefficient is chosen as one and symplectic factor as a small positive value. Experimental results show RAD outperforming nine baseline optimizers with five RL algorithms across twelve environments, including standard benchmarks and challenging scenarios. Notably, RAD achieves up to a 155.1% performance improvement over ADAM in Atari games, showcasing its efficacy in stabilizing and accelerating RL training.

Guiding Reinforcement Learning with Incomplete System Dynamics

Model-free reinforcement learning (RL) is inherently a reactive method, operating under the assumption that it starts with no prior knowledge of the system and entirely depends on trial-and-error for learning. This approach faces several challenges, such as poor sample efficiency, generalization, and the need for well-designed reward functions to guide learning effectively. On the other hand, controllers based on complete system dynamics do not require data. This paper addresses the intermediate situation where there is not enough model information for complete controller design, but there is enough to suggest that a model-free approach is not the best approach either. By carefully decoupling known and unknown information about the system dynamics, we obtain an embedded controller guided by our partial model and thus improve the learning efficiency of an RL-enhanced approach. A modular design allows us to deploy mainstream RL algorithms to refine the policy. Simulation results show that our method significantly improves sample efficiency compared with standard RL methods on continuous control tasks, and also offers enhanced performance over traditional control approaches. Experiments on a real ground vehicle also validate the performance of our method, including generalization and robustness.

Diffusion Actor-Critic with Entropy Regulator

Reinforcement learning (RL) has proven highly effective in addressing complex decision-making and control tasks. However, in most traditional RL algorithms, the policy is typically parameterized as a diagonal Gaussian distribution with learned mean and variance, which constrains their capability to acquire complex policies. In response to this problem, we propose an online RL algorithm termed diffusion actor-critic with entropy regulator (DACER). This algorithm conceptualizes the reverse process of the diffusion model as a novel policy function and leverages the capability of the diffusion model to fit multimodal distributions, thereby enhancing the representational capacity of the policy. Since the distribution of the diffusion policy lacks an analytical expression, its entropy cannot be determined analytically. To mitigate this, we propose a method to estimate the entropy of the diffusion policy utilizing Gaussian mixture model. Building on the estimated entropy, we can learn a parameter $\alpha$ that modulates the degree of exploration and exploitation. Parameter $\alpha$ will be employed to adaptively regulate the variance of the added noise, which is applied to the action output by the diffusion model. Experimental trials on MuJoCo benchmarks and a multimodal task demonstrate that the DACER algorithm achieves state-of-the-art (SOTA) performance in most MuJoCo control tasks while exhibiting a stronger representational capacity of the diffusion policy.

Policy Bifurcation in Safe Reinforcement Learning

Safe reinforcement learning (RL) offers advanced solutions to constrained optimal control problems. Existing studies in safe RL implicitly assume continuity in policy functions, where policies map states to actions in a smooth, uninterrupted manner; however, our research finds that in some scenarios, the feasible policy should be discontinuous or multi-valued, interpolating between discontinuous local optima can inevitably lead to constraint violations. We are the first to identify the generating mechanism of such a phenomenon, and employ topological analysis to rigorously prove the existence of policy bifurcation in safe RL, which corresponds to the contractibility of the reachable tuple. Our theorem reveals that in scenarios where the obstacle-free state space is non-simply connected, a feasible policy is required to be bifurcated, meaning its output action needs to change abruptly in response to the varying state. To train such a bifurcated policy, we propose a safe RL algorithm called multimodal policy optimization (MUPO), which utilizes a Gaussian mixture distribution as the policy output. The bifurcated behavior can be achieved by selecting the Gaussian component with the highest mixing coefficient. Besides, MUPO also integrates spectral normalization and forward KL divergence to enhance the policy's capability of exploring different modes. Experiments with vehicle control tasks show that our algorithm successfully learns the bifurcated policy and ensures satisfying safety, while a continuous policy suffers from inevitable constraint violations.

Integrated Drill Boom Hole-Seeking Control via Reinforcement Learning

Intelligent drill boom hole-seeking is a promising technology for enhancing drilling efficiency, mitigating potential safety hazards, and relieving human operators. Most existing intelligent drill boom control methods rely on a hierarchical control framework based on inverse kinematics. However, these methods are generally time-consuming due to the computational complexity of inverse kinematics and the inefficiency of the sequential execution of multiple joints. To tackle these challenges, this study proposes an integrated drill boom control method based on Reinforcement Learning (RL). We develop an integrated drill boom control framework that utilizes a parameterized policy to directly generate control inputs for all joints at each time step, taking advantage of joint posture and target hole information. By formulating the hole-seeking task as a Markov decision process, contemporary mainstream RL algorithms can be directly employed to learn a hole-seeking policy, thus eliminating the need for inverse kinematics solutions and promoting cooperative multi-joint control. To enhance the drilling accuracy throughout the entire drilling process, we devise a state representation that combines Denavit-Hartenberg joint information and preview hole-seeking discrepancy data. Simulation results show that the proposed method significantly outperforms traditional methods in terms of hole-seeking accuracy and time efficiency.