CycleINR: Cycle Implicit Neural Representation for Arbitrary-Scale Volumetric Super-Resolution of Medical Data

In the realm of medical 3D data, such as CT and MRI images, prevalent anisotropic resolution is characterized by high intra-slice but diminished inter-slice resolution. The lowered resolution between adjacent slices poses challenges, hindering optimal viewing experiences and impeding the development of robust downstream analysis algorithms. Various volumetric super-resolution algorithms aim to surmount these challenges, enhancing inter-slice resolution and overall 3D medical imaging quality. However, existing approaches confront inherent challenges: 1) often tailored to specific upsampling factors, lacking flexibility for diverse clinical scenarios; 2) newly generated slices frequently suffer from over-smoothing, degrading fine details, and leading to inter-slice inconsistency. In response, this study presents CycleINR, a novel enhanced Implicit Neural Representation model for 3D medical data volumetric super-resolution. Leveraging the continuity of the learned implicit function, the CycleINR model can achieve results with arbitrary up-sampling rates, eliminating the need for separate training. Additionally, we enhance the grid sampling in CycleINR with a local attention mechanism and mitigate over-smoothing by integrating cycle-consistent loss. We introduce a new metric, Slice-wise Noise Level Inconsistency (SNLI), to quantitatively assess inter-slice noise level inconsistency. The effectiveness of our approach is demonstrated through image quality evaluations on an in-house dataset and a downstream task analysis on the Medical Segmentation Decathlon liver tumor dataset.

Towards a Comprehensive, Efficient and Promptable Anatomic Structure Segmentation Model using 3D Whole-body CT Scans

Segment anything model (SAM) demonstrates strong generalization ability on natural image segmentation. However, its direct adaption in medical image segmentation tasks shows significant performance drops with inferior accuracy and unstable results. It may also requires an excessive number of prompt points to obtain a reasonable accuracy. For segmenting 3D radiological CT or MRI scans, a 2D SAM model has to separately handle hundreds of 2D slices. Although quite a few studies explore adapting SAM into medical image volumes, the efficiency of 2D adaption methods is unsatisfactory and 3D adaptation methods only capable of segmenting specific organs/tumors. In this work, we propose a comprehensive and scalable 3D SAM model for whole-body CT segmentation, named CT-SAM3D. Instead of adapting SAM, we propose a 3D promptable segmentation model using a (nearly) fully labeled CT dataset. To train CT-SAM3D effectively, ensuring the model's accurate responses to higher-dimensional spatial prompts is crucial, and 3D patch-wise training is required due to GPU memory constraints. For this purpose, we propose two key technical developments: 1) a progressively and spatially aligned prompt encoding method to effectively encode click prompts in local 3D space; and 2) a cross-patch prompt learning scheme to capture more 3D spatial context, which is beneficial for reducing the editing workloads when interactively prompting on large organs. CT-SAM3D is trained and validated using a curated dataset of 1204 CT scans containing 107 whole-body anatomies, reporting significantly better quantitative performance against all previous SAM-derived models by a large margin with much fewer click prompts. Our model can handle segmenting unseen organ as well. Code, data, and our 3D interactive segmentation tool with quasi-real-time responses will be made publicly available.

Anatomical Invariance Modeling and Semantic Alignment for Self-supervised Learning in 3D Medical Image Segmentation

Self-supervised learning (SSL) has recently achieved promising performance for 3D medical image segmentation tasks. Most current methods follow existing SSL paradigm originally designed for photographic or natural images, which cannot explicitly and thoroughly exploit the intrinsic similar anatomical structures across varying medical images. This may in fact degrade the quality of learned deep representations by maximizing the similarity among features containing spatial misalignment information and different anatomical semantics. In this work, we propose a new self-supervised learning framework, namely Alice, that explicitly fulfills Anatomical invariance modeling and semantic alignment via elaborately combining discriminative and generative objectives. Alice introduces a new contrastive learning strategy which encourages the similarity between views that are diversely mined but with consistent high-level semantics, in order to learn invariant anatomical features. Moreover, we design a conditional anatomical feature alignment module to complement corrupted embeddings with globally matched semantics and inter-patch topology information, conditioned by the distribution of local image content, which permits to create better contrastive pairs. Our extensive quantitative experiments on two public 3D medical image segmentation benchmarks of FLARE 2022 and BTCV demonstrate and validate the performance superiority of Alice, surpassing the previous best SSL counterpart methods by 2.11% and 1.77% in Dice coefficients, respectively.

Med-Query: Steerable Parsing of 9-DoF Medical Anatomies with Query Embedding

Automatic parsing of human anatomies at instance-level from 3D computed tomography (CT) scans is a prerequisite step for many clinical applications. The presence of pathologies, broken structures or limited field-of-view (FOV) all can make anatomy parsing algorithms vulnerable. In this work, we explore how to exploit and conduct the prosperous detection-then-segmentation paradigm in 3D medical data, and propose a steerable, robust, and efficient computing framework for detection, identification, and segmentation of anatomies in CT scans. Considering complicated shapes, sizes and orientations of anatomies, without lose of generality, we present the nine degrees-of-freedom (9-DoF) pose estimation solution in full 3D space using a novel single-stage, non-hierarchical forward representation. Our whole framework is executed in a steerable manner where any anatomy of interest can be directly retrieved to further boost the inference efficiency. We have validated the proposed method on three medical imaging parsing tasks of ribs, spine, and abdominal organs. For rib parsing, CT scans have been annotated at the rib instance-level for quantitative evaluation, similarly for spine vertebrae and abdominal organs. Extensive experiments on 9-DoF box detection and rib instance segmentation demonstrate the effectiveness of our framework (with the identification rate of 97.0% and the segmentation Dice score of 90.9%) in high efficiency, compared favorably against several strong baselines (e.g., CenterNet, FCOS, and nnU-Net). For spine identification and segmentation, our method achieves a new state-of-the-art result on the public CTSpine1K dataset. Last, we report highly competitive results in multi-organ segmentation at FLARE22 competition. Our annotations, code and models will be made publicly available at: https://github.com/alibaba-damo-academy/Med_Query.

NeuralMPS: Non-Lambertian Multispectral Photometric Stereo via Spectral Reflectance Decomposition

Multispectral photometric stereo(MPS) aims at recovering the surface normal of a scene from a single-shot multispectral image captured under multispectral illuminations. Existing MPS methods adopt the Lambertian reflectance model to make the problem tractable, but it greatly limits their application to real-world surfaces. In this paper, we propose a deep neural network named NeuralMPS to solve the MPS problem under general non-Lambertian spectral reflectances. Specifically, we present a spectral reflectance decomposition(SRD) model to disentangle the spectral reflectance into geometric components and spectral components. With this decomposition, we show that the MPS problem for surfaces with a uniform material is equivalent to the conventional photometric stereo(CPS) with unknown light intensities. In this way, NeuralMPS reduces the difficulty of the non-Lambertian MPS problem by leveraging the well-studied non-Lambertian CPS methods. Experiments on both synthetic and real-world scenes demonstrate the effectiveness of our method.

A Reinforcement Learning Framework with Description Language for Critical Driving Scenario Generation

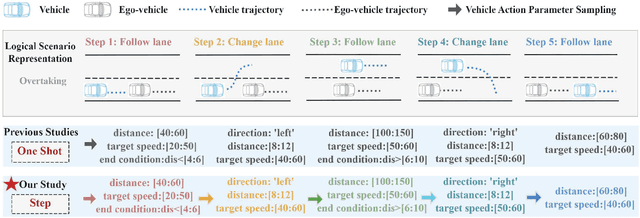
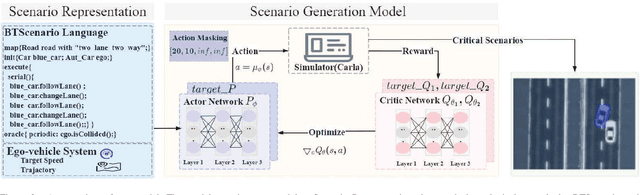
Critical scenario generation requires the ability of finding critical parameter combinations from the infinite parameter space in the logic scenario. Existing solutions aims to explore the correlation of parameters in the initial scenario without considering the connection between the parameters in the action sequence. How to model action sequences and consider the effects of different action parameter in the scenario remains a key challenge to solve the problem. In this paper, we propose a framework to generate critical scenarios for speeding up evaluating specific tasks. Specifically, we first propose a description language, BTScenario, to model the scenario, which contains the map, actors, interactions between actors, and oracles. We then use reinforcement learning to search for combinations of critical parameters. By adopting the action mask, the effects of non-fixed length and sequences in parameter space can be prevented. We demonstrate that the proposed framework is more efficient than random test and combination test methods in various scenarios.

A New Probabilistic V-Net Model with Hierarchical Spatial Feature Transform for Efficient Abdominal Multi-Organ Segmentation

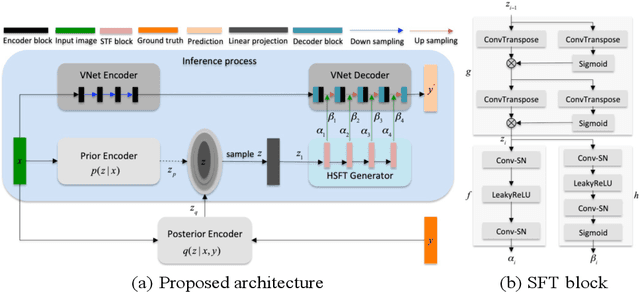
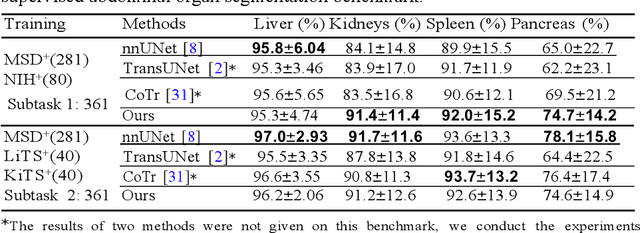
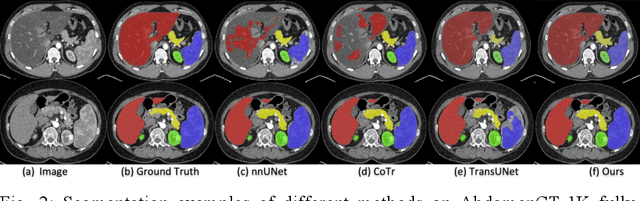
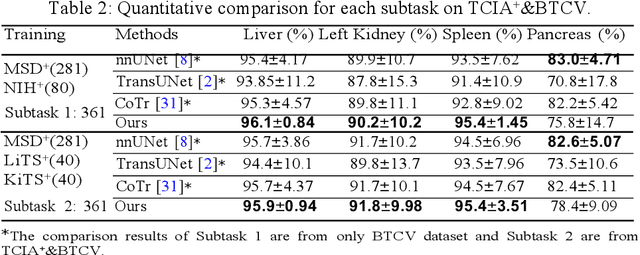
Accurate and robust abdominal multi-organ segmentation from CT imaging of different modalities is a challenging task due to complex inter- and intra-organ shape and appearance variations among abdominal organs. In this paper, we propose a probabilistic multi-organ segmentation network with hierarchical spatial-wise feature modulation to capture flexible organ semantic variants and inject the learnt variants into different scales of feature maps for guiding segmentation. More specifically, we design an input decomposition module via a conditional variational auto-encoder to learn organ-specific distributions on the low dimensional latent space and model richer organ semantic variations that is conditioned on input images.Then by integrating these learned variations into the V-Net decoder hierarchically via spatial feature transformation, which has the ability to convert the variations into conditional Affine transformation parameters for spatial-wise feature maps modulating and guiding the fine-scale segmentation. The proposed method is trained on the publicly available AbdomenCT-1K dataset and evaluated on two other open datasets, i.e., 100 challenging/pathological testing patient cases from AbdomenCT-1K fully-supervised abdominal organ segmentation benchmark and 90 cases from TCIA+&BTCV dataset. Highly competitive or superior quantitative segmentation results have been achieved using these datasets for four abdominal organs of liver, kidney, spleen and pancreas with reported Dice scores improved by 7.3% for kidneys and 9.7% for pancreas, while being ~7 times faster than two strong baseline segmentation methods(nnUNet and CoTr).

Edge-preserving Near-light Photometric Stereo with Neural Surfaces

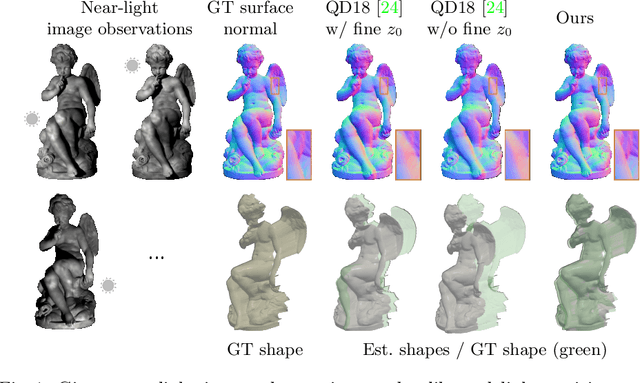
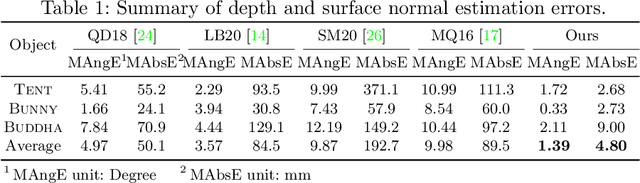
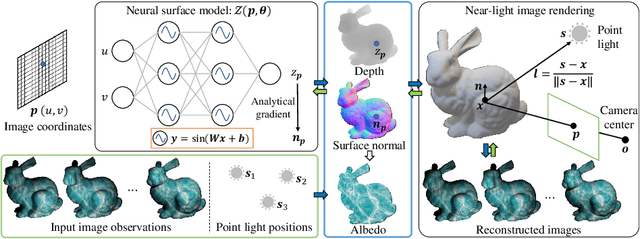
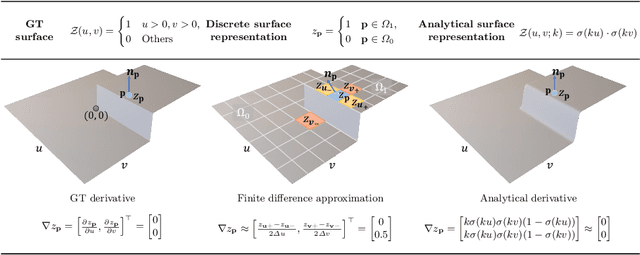
This paper presents a near-light photometric stereo method that faithfully preserves sharp depth edges in the 3D reconstruction. Unlike previous methods that rely on finite differentiation for approximating depth partial derivatives and surface normals, we introduce an analytically differentiable neural surface in near-light photometric stereo for avoiding differentiation errors at sharp depth edges, where the depth is represented as a neural function of the image coordinates. By further formulating the Lambertian albedo as a dependent variable resulting from the surface normal and depth, our method is insusceptible to inaccurate depth initialization. Experiments on both synthetic and real-world scenes demonstrate the effectiveness of our method for detailed shape recovery with edge preservation.

End-to-end Robustness for Sensing-Reasoning Machine Learning Pipelines

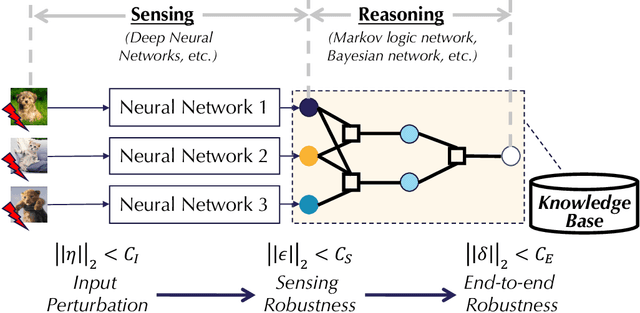
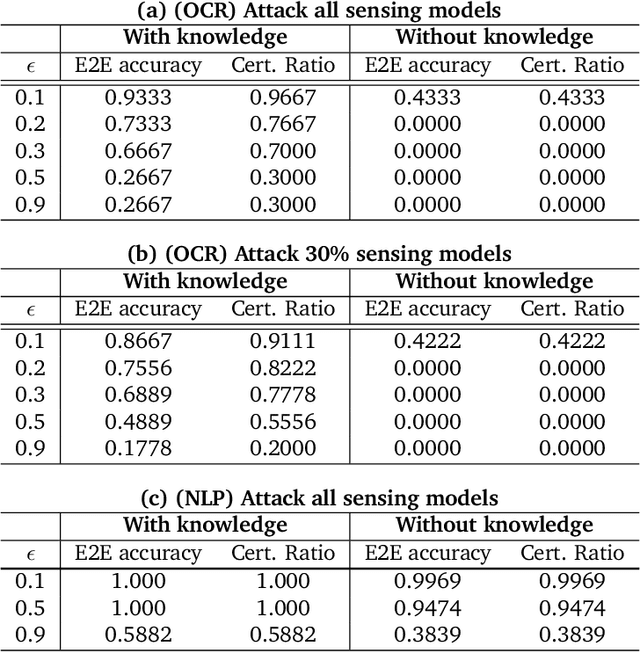
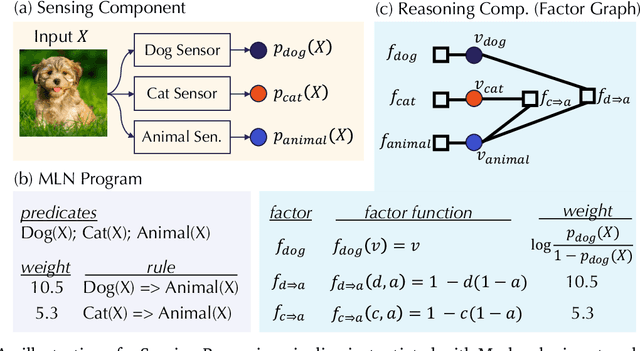
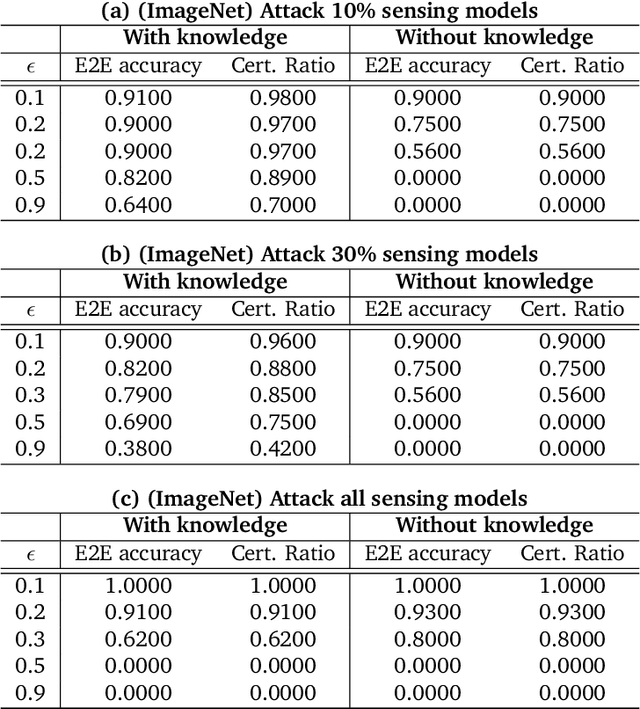
As machine learning (ML) being applied to many mission-critical scenarios, certifying ML model robustness becomes increasingly important. Many previous works focuses on the robustness of independent ML and ensemble models, and can only certify a very small magnitude of the adversarial perturbation. In this paper, we take a different viewpoint and improve learning robustness by going beyond independent ML and ensemble models. We aim at promoting the generic Sensing-Reasoning machine learning pipeline which contains both the sensing (e.g. deep neural networks) and reasoning (e.g. Markov logic networks (MLN)) components enriched with domain knowledge. Can domain knowledge help improve learning robustness? Can we formally certify the end-to-end robustness of such an ML pipeline? We first theoretically analyze the computational complexity of checking the provable robustness in the reasoning component. We then derive the provable robustness bound for several concrete reasoning components. We show that for reasoning components such as MLN and a specific family of Bayesian networks it is possible to certify the robustness of the whole pipeline even with a large magnitude of perturbation which cannot be certified by existing work. Finally, we conduct extensive real-world experiments on large scale datasets to evaluate the certified robustness for Sensing-Reasoning ML pipelines.

Towards a Fast Steady-State Visual Evoked Potentials Brain-Computer Interface

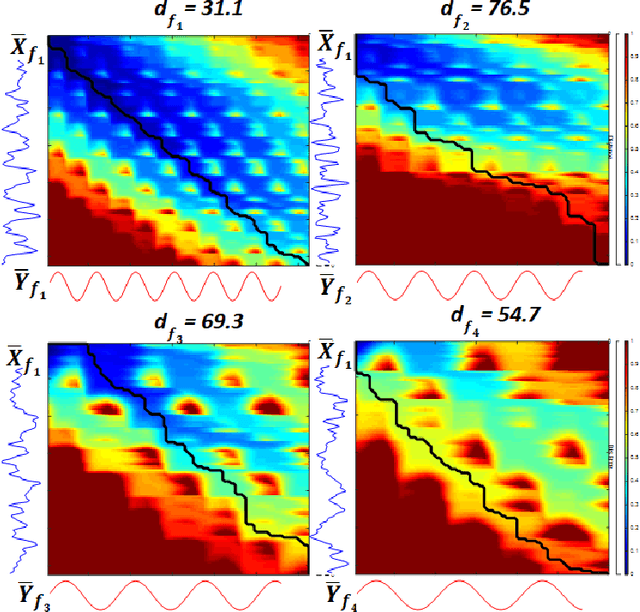
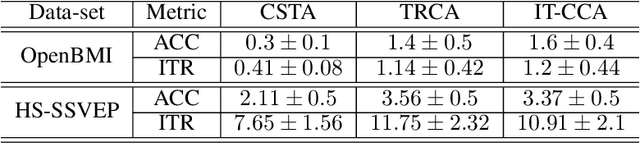
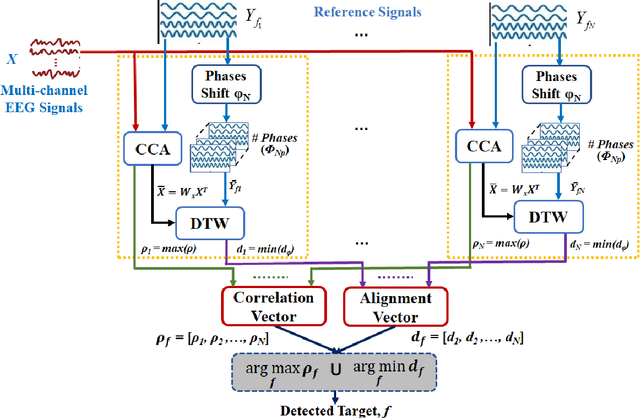
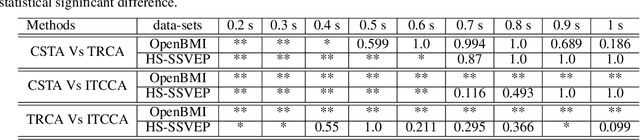
Steady-state visual evoked potentials (SSVEP) brain-computer interface (BCI) provides reliable responses leading to high accuracy and information throughput. But achieving high accuracy typically requires a relatively long time window of one second or more. Various methods were proposed to improve sub-second response accuracy through subject-specific training and calibration. Substantial performance improvements were achieved with tedious calibration and subject-specific training; resulting in the user's discomfort. So, we propose a training-free method by combining spatial-filtering and temporal alignment (CSTA) to recognize SSVEP responses in sub-second response time. CSTA exploits linear correlation and non-linear similarity between steady-state responses and stimulus templates with complementary fusion to achieve desirable performance improvements. We evaluated the performance of CSTA in terms of accuracy and Information Transfer Rate (ITR) in comparison with both training-based and training-free methods using two SSVEP data-sets. We observed that CSTA achieves the maximum mean accuracy of 97.43$\pm$2.26 % and 85.71$\pm$13.41 % with four-class and forty-class SSVEP data-sets respectively in sub-second response time in offline analysis. CSTA yields significantly higher mean performance (p<0.001) than the training-free method on both data-sets. Compared with training-based methods, CSTA shows 29.33$\pm$19.65 % higher mean accuracy with statistically significant differences in time window less than 0.5 s. In longer time windows, CSTA exhibits either better or comparable performance though not statistically significantly better than training-based methods. We show that the proposed method brings advantages of subject-independent SSVEP classification without requiring training while enabling high target recognition performance in sub-second response time.