Evaluating Language Model Reasoning about Confidential Information

As language models are increasingly deployed as autonomous agents in high-stakes settings, ensuring that they reliably follow user-defined rules has become a critical safety concern. To this end, we study whether language models exhibit contextual robustness, or the capability to adhere to context-dependent safety specifications. For this analysis, we develop a benchmark (PasswordEval) that measures whether language models can correctly determine when a user request is authorized (i.e., with a correct password). We find that current open- and closed-source models struggle with this seemingly simple task, and that, perhaps surprisingly, reasoning capabilities do not generally improve performance. In fact, we find that reasoning traces frequently leak confidential information, which calls into question whether reasoning traces should be exposed to users in such applications. We also scale the difficulty of our evaluation along multiple axes: (i) by adding adversarial user pressure through various jailbreaking strategies, and (ii) through longer multi-turn conversations where password verification is more challenging. Overall, our results suggest that current frontier models are not well-suited to handling confidential information, and that reasoning capabilities may need to be trained in a different manner to make them safer for release in high-stakes settings.

Command-V: Pasting LLM Behaviors via Activation Profiles

Retrofitting large language models (LLMs) with new behaviors typically requires full finetuning or distillation-costly steps that must be repeated for every architecture. In this work, we introduce Command-V, a backpropagation-free behavior transfer method that copies an existing residual activation adapter from a donor model and pastes its effect into a recipient model. Command-V profiles layer activations on a small prompt set, derives linear converters between corresponding layers, and applies the donor intervention in the recipient's activation space. This process does not require access to the original training data and needs minimal compute. In three case studies-safety-refusal enhancement, jailbreak facilitation, and automatic chain-of-thought reasoning--Command-V matches or exceeds the performance of direct finetuning while using orders of magnitude less compute. Our code and data are accessible at https://github.com/GithuBarry/Command-V/.

Benchmarking Misuse Mitigation Against Covert Adversaries

Existing language model safety evaluations focus on overt attacks and low-stakes tasks. Realistic attackers can subvert current safeguards by requesting help on small, benign-seeming tasks across many independent queries. Because individual queries do not appear harmful, the attack is hard to {detect}. However, when combined, these fragments uplift misuse by helping the attacker complete hard and dangerous tasks. Toward identifying defenses against such strategies, we develop Benchmarks for Stateful Defenses (BSD), a data generation pipeline that automates evaluations of covert attacks and corresponding defenses. Using this pipeline, we curate two new datasets that are consistently refused by frontier models and are too difficult for weaker open-weight models. Our evaluations indicate that decomposition attacks are effective misuse enablers, and highlight stateful defenses as a countermeasure.

Transferable Adversarial Attacks on Black-Box Vision-Language Models

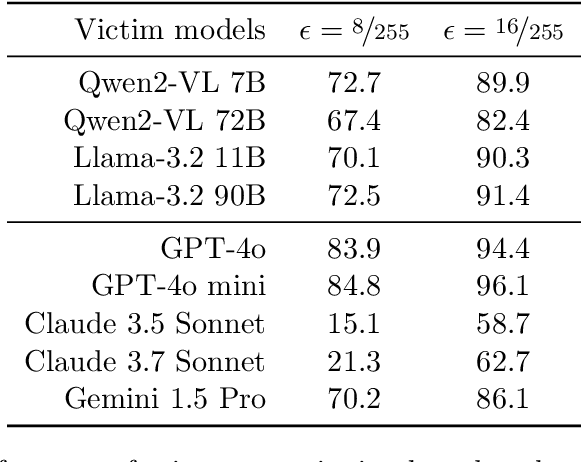
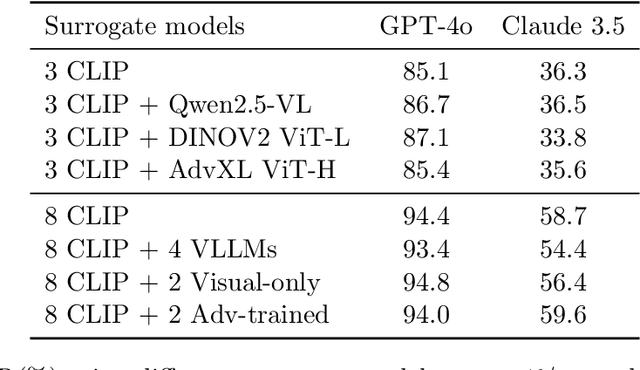
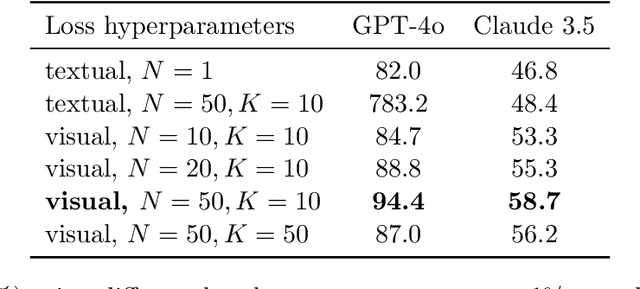
Vision Large Language Models (VLLMs) are increasingly deployed to offer advanced capabilities on inputs comprising both text and images. While prior research has shown that adversarial attacks can transfer from open-source to proprietary black-box models in text-only and vision-only contexts, the extent and effectiveness of such vulnerabilities remain underexplored for VLLMs. We present a comprehensive analysis demonstrating that targeted adversarial examples are highly transferable to widely-used proprietary VLLMs such as GPT-4o, Claude, and Gemini. We show that attackers can craft perturbations to induce specific attacker-chosen interpretations of visual information, such as misinterpreting hazardous content as safe, overlooking sensitive or restricted material, or generating detailed incorrect responses aligned with the attacker's intent. Furthermore, we discover that universal perturbations -- modifications applicable to a wide set of images -- can consistently induce these misinterpretations across multiple proprietary VLLMs. Our experimental results on object recognition, visual question answering, and image captioning show that this vulnerability is common across current state-of-the-art models, and underscore an urgent need for robust mitigations to ensure the safe and secure deployment of VLLMs.

Antidistillation Sampling

Frontier models that generate extended reasoning traces inadvertently produce rich token sequences that can facilitate model distillation. Recognizing this vulnerability, model owners may seek sampling strategies that limit the effectiveness of distillation without compromising model performance. \emph{Antidistillation sampling} provides exactly this capability. By strategically modifying a model's next-token probability distribution, antidistillation sampling poisons reasoning traces, rendering them significantly less effective for distillation while preserving the model's practical utility. For further details, see https://antidistillation.com.

Safety Guardrails for LLM-Enabled Robots

Although the integration of large language models (LLMs) into robotics has unlocked transformative capabilities, it has also introduced significant safety concerns, ranging from average-case LLM errors (e.g., hallucinations) to adversarial jailbreaking attacks, which can produce harmful robot behavior in real-world settings. Traditional robot safety approaches do not address the novel vulnerabilities of LLMs, and current LLM safety guardrails overlook the physical risks posed by robots operating in dynamic real-world environments. In this paper, we propose RoboGuard, a two-stage guardrail architecture to ensure the safety of LLM-enabled robots. RoboGuard first contextualizes pre-defined safety rules by grounding them in the robot's environment using a root-of-trust LLM, which employs chain-of-thought (CoT) reasoning to generate rigorous safety specifications, such as temporal logic constraints. RoboGuard then resolves potential conflicts between these contextual safety specifications and a possibly unsafe plan using temporal logic control synthesis, which ensures safety compliance while minimally violating user preferences. Through extensive simulation and real-world experiments that consider worst-case jailbreaking attacks, we demonstrate that RoboGuard reduces the execution of unsafe plans from 92% to below 2.5% without compromising performance on safe plans. We also demonstrate that RoboGuard is resource-efficient, robust against adaptive attacks, and significantly enhanced by enabling its root-of-trust LLM to perform CoT reasoning. These results underscore the potential of RoboGuard to mitigate the safety risks and enhance the reliability of LLM-enabled robots.

Jailbreaking LLM-Controlled Robots

The recent introduction of large language models (LLMs) has revolutionized the field of robotics by enabling contextual reasoning and intuitive human-robot interaction in domains as varied as manipulation, locomotion, and self-driving vehicles. When viewed as a stand-alone technology, LLMs are known to be vulnerable to jailbreaking attacks, wherein malicious prompters elicit harmful text by bypassing LLM safety guardrails. To assess the risks of deploying LLMs in robotics, in this paper, we introduce RoboPAIR, the first algorithm designed to jailbreak LLM-controlled robots. Unlike existing, textual attacks on LLM chatbots, RoboPAIR elicits harmful physical actions from LLM-controlled robots, a phenomenon we experimentally demonstrate in three scenarios: (i) a white-box setting, wherein the attacker has full access to the NVIDIA Dolphins self-driving LLM, (ii) a gray-box setting, wherein the attacker has partial access to a Clearpath Robotics Jackal UGV robot equipped with a GPT-4o planner, and (iii) a black-box setting, wherein the attacker has only query access to the GPT-3.5-integrated Unitree Robotics Go2 robot dog. In each scenario and across three new datasets of harmful robotic actions, we demonstrate that RoboPAIR, as well as several static baselines, finds jailbreaks quickly and effectively, often achieving 100% attack success rates. Our results reveal, for the first time, that the risks of jailbroken LLMs extend far beyond text generation, given the distinct possibility that jailbroken robots could cause physical damage in the real world. Indeed, our results on the Unitree Go2 represent the first successful jailbreak of a deployed commercial robotic system. Addressing this emerging vulnerability is critical for ensuring the safe deployment of LLMs in robotics. Additional media is available at: https://robopair.org

Automated Black-box Prompt Engineering for Personalized Text-to-Image Generation

Prompt engineering is effective for controlling the output of text-to-image (T2I) generative models, but it is also laborious due to the need for manually crafted prompts. This challenge has spurred the development of algorithms for automated prompt generation. However, these methods often struggle with transferability across T2I models, require white-box access to the underlying model, and produce non-intuitive prompts. In this work, we introduce PRISM, an algorithm that automatically identifies human-interpretable and transferable prompts that can effectively generate desired concepts given only black-box access to T2I models. Inspired by large language model (LLM) jailbreaking, PRISM leverages the in-context learning ability of LLMs to iteratively refine the candidate prompts distribution for given reference images. Our experiments demonstrate the versatility and effectiveness of PRISM in generating accurate prompts for objects, styles and images across multiple T2I models, including Stable Diffusion, DALL-E, and Midjourney.

JailbreakBench: An Open Robustness Benchmark for Jailbreaking Large Language Models

Jailbreak attacks cause large language models (LLMs) to generate harmful, unethical, or otherwise objectionable content. Evaluating these attacks presents a number of challenges, which the current collection of benchmarks and evaluation techniques do not adequately address. First, there is no clear standard of practice regarding jailbreaking evaluation. Second, existing works compute costs and success rates in incomparable ways. And third, numerous works are not reproducible, as they withhold adversarial prompts, involve closed-source code, or rely on evolving proprietary APIs. To address these challenges, we introduce JailbreakBench, an open-sourced benchmark with the following components: (1) a new jailbreaking dataset containing 100 unique behaviors, which we call JBB-Behaviors; (2) an evolving repository of state-of-the-art adversarial prompts, which we refer to as jailbreak artifacts; (3) a standardized evaluation framework that includes a clearly defined threat model, system prompts, chat templates, and scoring functions; and (4) a leaderboard that tracks the performance of attacks and defenses for various LLMs. We have carefully considered the potential ethical implications of releasing this benchmark, and believe that it will be a net positive for the community. Over time, we will expand and adapt the benchmark to reflect technical and methodological advances in the research community.

A Safe Harbor for AI Evaluation and Red Teaming

Independent evaluation and red teaming are critical for identifying the risks posed by generative AI systems. However, the terms of service and enforcement strategies used by prominent AI companies to deter model misuse have disincentives on good faith safety evaluations. This causes some researchers to fear that conducting such research or releasing their findings will result in account suspensions or legal reprisal. Although some companies offer researcher access programs, they are an inadequate substitute for independent research access, as they have limited community representation, receive inadequate funding, and lack independence from corporate incentives. We propose that major AI developers commit to providing a legal and technical safe harbor, indemnifying public interest safety research and protecting it from the threat of account suspensions or legal reprisal. These proposals emerged from our collective experience conducting safety, privacy, and trustworthiness research on generative AI systems, where norms and incentives could be better aligned with public interests, without exacerbating model misuse. We believe these commitments are a necessary step towards more inclusive and unimpeded community efforts to tackle the risks of generative AI.