A Simple and Efficient Sampling-based Algorithm for General Reachability Analysis

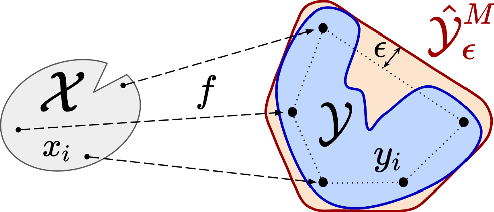
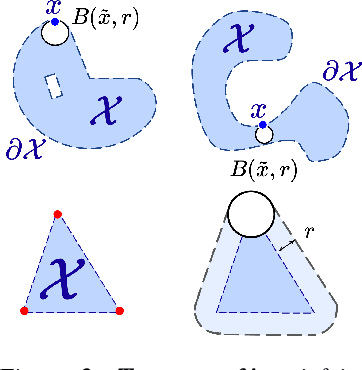
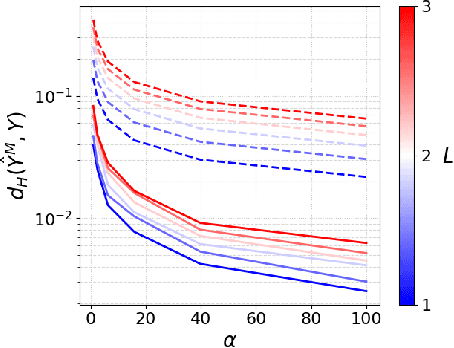
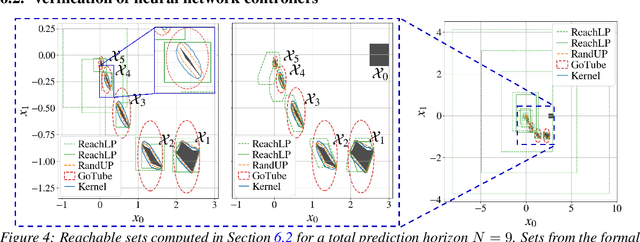
In this work, we analyze an efficient sampling-based algorithm for general-purpose reachability analysis, which remains a notoriously challenging problem with applications ranging from neural network verification to safety analysis of dynamical systems. By sampling inputs, evaluating their images in the true reachable set, and taking their $\epsilon$-padded convex hull as a set estimator, this algorithm applies to general problem settings and is simple to implement. Our main contribution is the derivation of asymptotic and finite-sample accuracy guarantees using random set theory. This analysis informs algorithmic design to obtain an $\epsilon$-close reachable set approximation with high probability, provides insights into which reachability problems are most challenging, and motivates safety-critical applications of the technique. On a neural network verification task, we show that this approach is more accurate and significantly faster than prior work. Informed by our analysis, we also design a robust model predictive controller that we demonstrate in hardware experiments.

On the Problem of Reformulating Systems with Uncertain Dynamics as a Stochastic Differential Equation

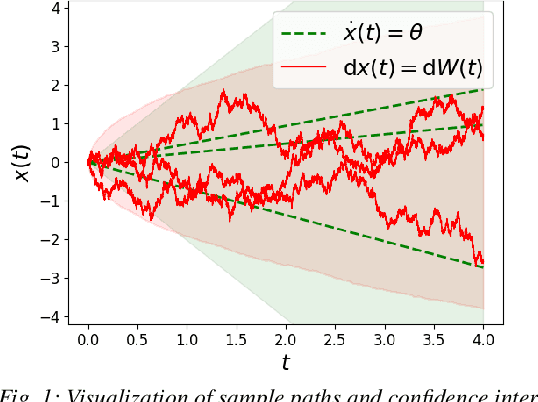
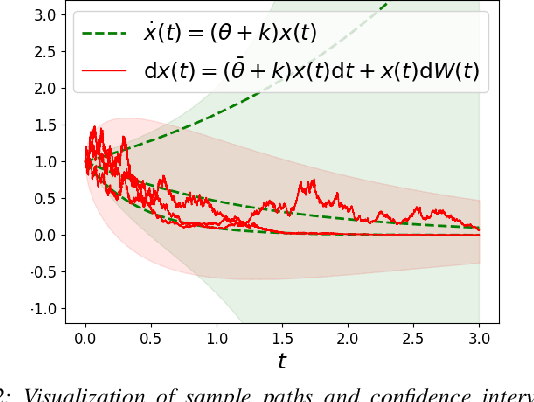
We identify an issue in recent approaches to learning-based control that reformulate systems with uncertain dynamics using a stochastic differential equation. Specifically, we discuss the approximation that replaces a model with fixed but uncertain parameters (a source of epistemic uncertainty) with a model subject to external disturbances modeled as a Brownian motion (corresponding to aleatoric uncertainty).

Convex Optimization for Trajectory Generation

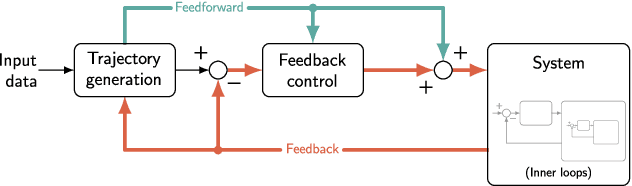
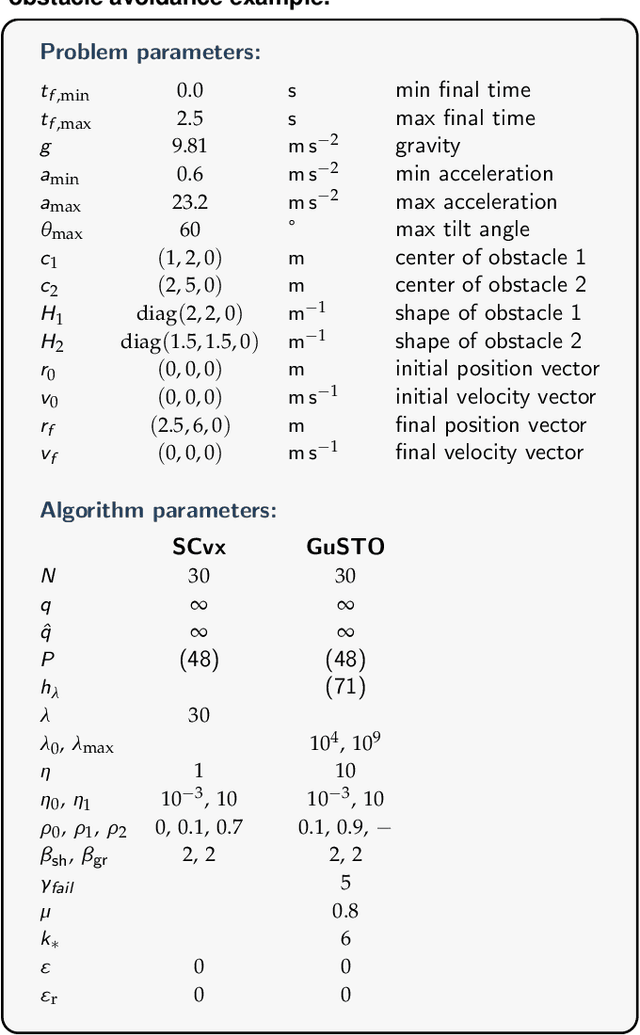
Reliable and efficient trajectory generation methods are a fundamental need for autonomous dynamical systems of tomorrow. The goal of this article is to provide a comprehensive tutorial of three major convex optimization-based trajectory generation methods: lossless convexification (LCvx), and two sequential convex programming algorithms known as SCvx and GuSTO. In this article, trajectory generation is the computation of a dynamically feasible state and control signal that satisfies a set of constraints while optimizing key mission objectives. The trajectory generation problem is almost always nonconvex, which typically means that it is not readily amenable to efficient and reliable solution onboard an autonomous vehicle. The three algorithms that we discuss use problem reformulation and a systematic algorithmic strategy to nonetheless solve nonconvex trajectory generation tasks through the use of a convex optimizer. The theoretical guarantees and computational speed offered by convex optimization have made the algorithms popular in both research and industry circles. To date, the list of applications includes rocket landing, spacecraft hypersonic reentry, spacecraft rendezvous and docking, aerial motion planning for fixed-wing and quadrotor vehicles, robot motion planning, and more. Among these applications are high-profile rocket flights conducted by organizations like NASA, Masten Space Systems, SpaceX, and Blue Origin. This article aims to give the reader the tools and understanding necessary to work with each algorithm, and to know what each method can and cannot do. A publicly available source code repository supports the provided numerical examples. By the end of the article, the reader should be ready to use the methods, to extend them, and to contribute to their many exciting modern applications.

NeBula: Quest for Robotic Autonomy in Challenging Environments; TEAM CoSTAR at the DARPA Subterranean Challenge

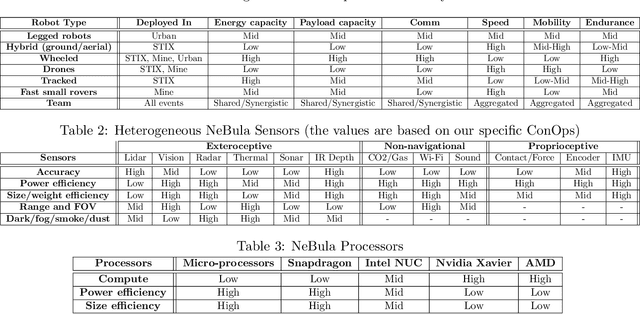
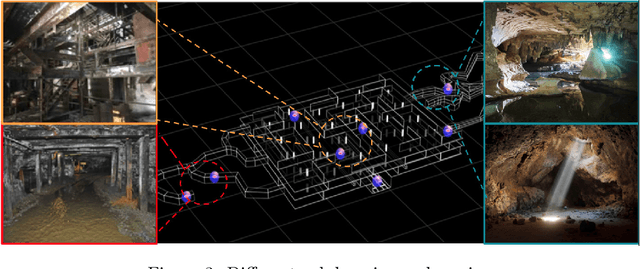
This paper presents and discusses algorithms, hardware, and software architecture developed by the TEAM CoSTAR (Collaborative SubTerranean Autonomous Robots), competing in the DARPA Subterranean Challenge. Specifically, it presents the techniques utilized within the Tunnel (2019) and Urban (2020) competitions, where CoSTAR achieved 2nd and 1st place, respectively. We also discuss CoSTAR's demonstrations in Martian-analog surface and subsurface (lava tubes) exploration. The paper introduces our autonomy solution, referred to as NeBula (Networked Belief-aware Perceptual Autonomy). NeBula is an uncertainty-aware framework that aims at enabling resilient and modular autonomy solutions by performing reasoning and decision making in the belief space (space of probability distributions over the robot and world states). We discuss various components of the NeBula framework, including: (i) geometric and semantic environment mapping; (ii) a multi-modal positioning system; (iii) traversability analysis and local planning; (iv) global motion planning and exploration behavior; (i) risk-aware mission planning; (vi) networking and decentralized reasoning; and (vii) learning-enabled adaptation. We discuss the performance of NeBula on several robot types (e.g. wheeled, legged, flying), in various environments. We discuss the specific results and lessons learned from fielding this solution in the challenging courses of the DARPA Subterranean Challenge competition.

Analysis of Theoretical and Numerical Properties of Sequential Convex Programming for Continuous-Time Optimal Control

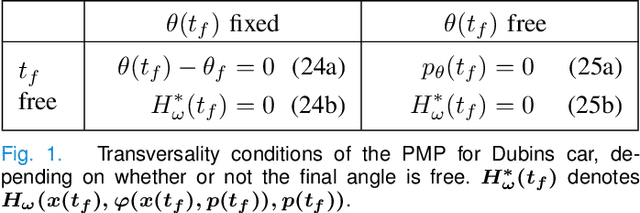
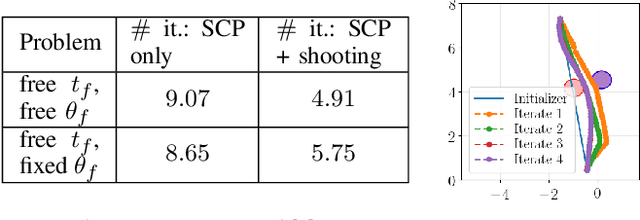
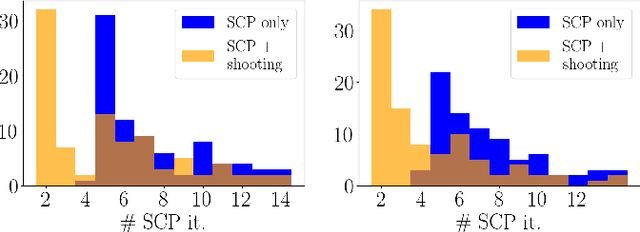
Through the years, Sequential Convex Programming (SCP) has gained great interest as an efficient tool for non-convex optimal control. Despite the large number of existing algorithmic frameworks, only a few are accompanied by rigorous convergence analysis, which are often only tailored to discrete-time problem formulations. In this paper, we present a unifying theoretical analysis of a fairly general class of SCP procedures which is applied to the original continuous-time formulation. Besides the extension of classical convergence guarantees to continuous-time settings, our analysis reveals two new features inherited by SCP-type methods. First, we show how one can more easily account for manifold-type constraints, which play a key role in the optimal control of mechanical systems. Second, we demonstrate how the theoretical analysis may be leveraged to devise an accelerated implementation of SCP based on indirect methods. Detailed numerical experiments are provided to show the key benefits of a continuous-time analysis to improve performance.

Safe Model-Based Meta-Reinforcement Learning: A Sequential Exploration-Exploitation Framework

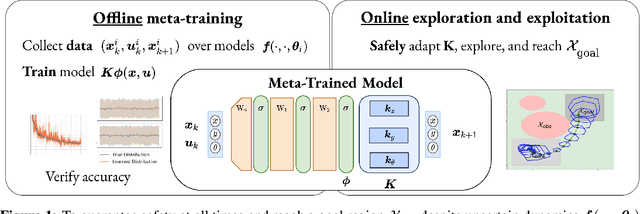
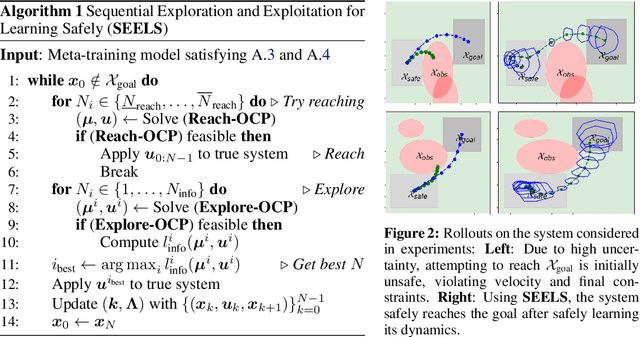
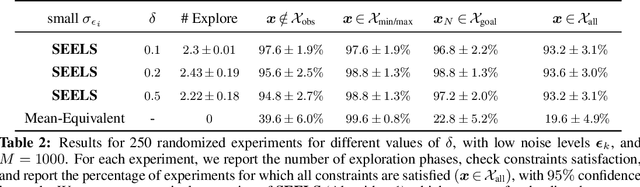
Safe deployment of autonomous robots in diverse environments requires agents that are capable of safe and efficient adaptation to new scenarios. Indeed, achieving both data efficiency and well-calibrated safety has been a central problem in robotic learning and adaptive control due in part to the tension between these objectives. In this work, we develop a framework for probabilistically safe operation with uncertain dynamics. This framework relies on Bayesian meta-learning for efficient inference of system dynamics with calibrated uncertainty. We leverage the model structure to construct confidence bounds which hold throughout the learning process, and factor this uncertainty into a model-based planning framework. By decomposing the problem of control under uncertainty into discrete exploration and exploitation phases, our framework extends to problems with high initial uncertainty while maintaining probabilistic safety and persistent feasibility guarantees during every phase of operation. We validate our approach on the problem of a nonlinear free flying space robot manipulating a payload in cluttered environments, and show it can safely learn and reach a goal.

Sampling-based Reachability Analysis: A Random Set Theory Approach with Adversarial Sampling

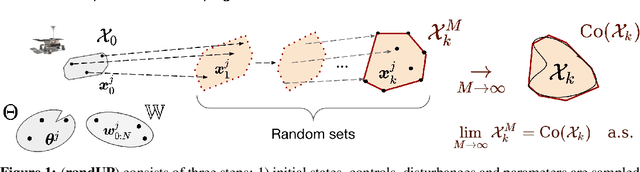
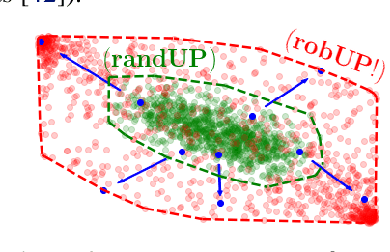
Reachability analysis is at the core of many applications, from neural network verification, to safe trajectory planning of uncertain systems. However, this problem is notoriously challenging, and current approaches tend to be either too restrictive, too slow, too conservative, or approximate and therefore lack guarantees. In this paper, we propose a simple yet effective sampling-based approach to perform reachability analysis for arbitrary dynamical systems. Our key novel idea consists of using random set theory to give a rigorous interpretation of our method, and prove that it returns sets which are guaranteed to converge to the convex hull of the true reachable sets. Additionally, we leverage recent work on robust deep learning and propose a new adversarial sampling approach to robustify our algorithm and accelerate its convergence. We show that our method is faster and less conservative than other approaches, present results for approximate reachability analysis of neural networks and robust trajectory optimization of high-dimensional uncertain nonlinear systems, and discuss future applications.

Contact Inertial Odometry: Collisions are your Friend

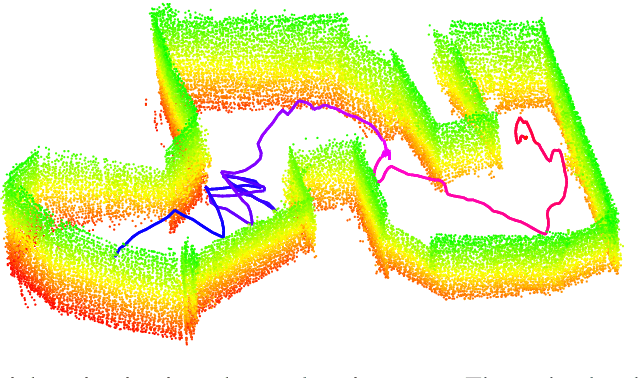
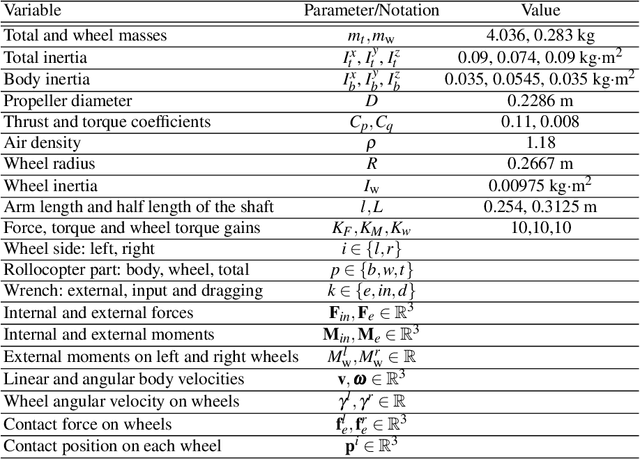
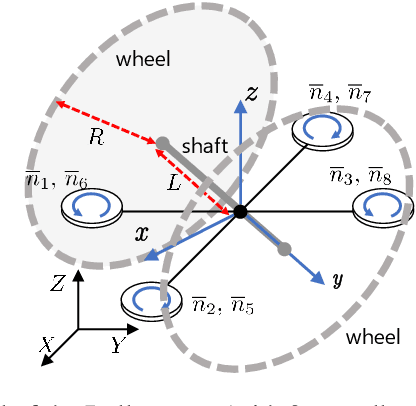
Autonomous exploration of unknown environments with aerial vehicles remains a challenging problem, especially in perceptually degraded conditions. Dust, smoke, fog, and a lack of visual or LiDAR-based features result in severe difficulties for state estimation and planning. The absence of measurement updates from visual or LiDAR odometry can cause large drifts in velocity estimates while propagating measurements from an IMU. Furthermore, it is not possible to construct a map for collision checking in absence of pose updates. In this work, we show that it is indeed possible to navigate without any exteroceptive sensing by exploiting collisions instead of treating them as constraints. To this end, we first perform modeling and system identification for a hybrid ground and aerial vehicle which can withstand collisions. Next, we develop a novel external wrench estimation algorithm for this class of vehicles. We then present a novel contact-based inertial odometry (CIO) algorithm: it uses estimated external forces to detect collisions and to generate pseudo-measurements of the robot velocity, fused in an Extended Kalman Filter. Finally, we implement a reactive planner and control law which encourage exploration by bouncing off obstacles. We validate our framework in hardware experiments and show that a quadrotor can traverse a cluttered environment using an IMU only. This work can be used on drones to recover from visual inertial odometry failure or on micro-drones that do not have the payload capacity to carry cameras, LiDARs or powerful computers.

Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach

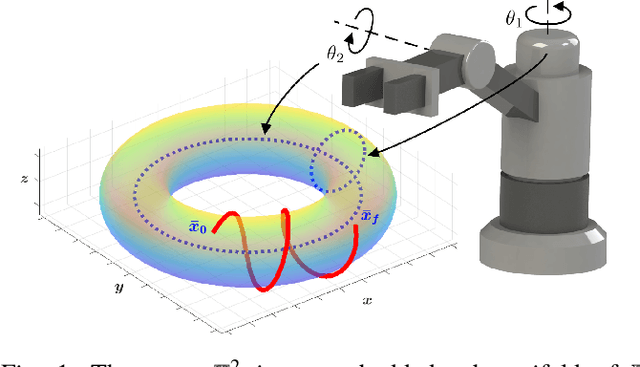
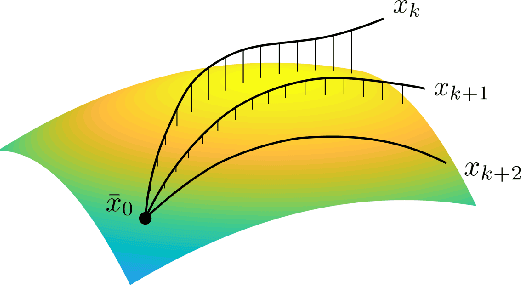
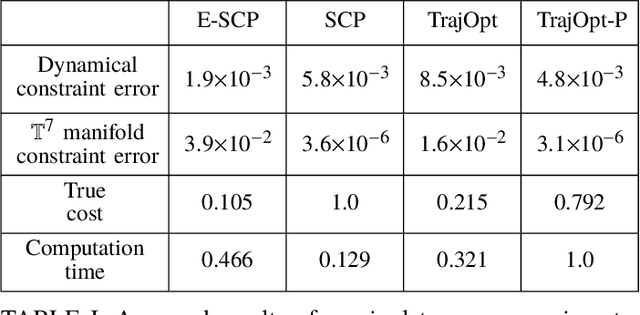
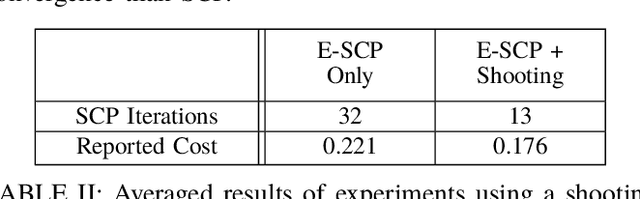
Sequential Convex Programming (SCP) has recently gained popularity as a tool for trajectory optimization due to its sound theoretical properties and practical performance. Yet, most SCP-based methods for trajectory optimization are restricted to Euclidean settings, which precludes their application to problem instances where one must reason about manifold-type constraints (that is, constraints, such as loop closure, which restrict the motion of a system to a subset of the ambient space). The aim of this paper is to fill this gap by extending SCP-based trajectory optimization methods to a manifold setting. The key insight is to leverage geometric embeddings to lift a manifold-constrained trajectory optimization problem into an equivalent problem defined over a space enjoying a Euclidean structure. This insight allows one to extend existing SCP methods to a manifold setting in a fairly natural way. In particular, we present a SCP algorithm for manifold problems with refined theoretical guarantees that resemble those derived for the Euclidean setting, and demonstrate its practical performance via numerical experiments.