Rethinking Diffusion Models with Symmetries through Canonicalization with Applications to Molecular Graph Generation

Many generative tasks in chemistry and science involve distributions invariant to group symmetries (e.g., permutation and rotation). A common strategy enforces invariance and equivariance through architectural constraints such as equivariant denoisers and invariant priors. In this paper, we challenge this tradition through the alternative canonicalization perspective: first map each sample to an orbit representative with a canonical pose or order, train an unconstrained (non-equivariant) diffusion or flow model on the canonical slice, and finally recover the invariant distribution by sampling a random symmetry transform at generation time. Building on a formal quotient-space perspective, our work provides a comprehensive theory of canonical diffusion by proving: (i) the correctness, universality and superior expressivity of canonical generative models over invariant targets; (ii) canonicalization accelerates training by removing diffusion score complexity induced by group mixtures and reducing conditional variance in flow matching. We then show that aligned priors and optimal transport act complementarily with canonicalization and further improves training efficiency. We instantiate the framework for molecular graph generation under $S_n \times SE(3)$ symmetries. By leveraging geometric spectra-based canonicalization and mild positional encodings, canonical diffusion significantly outperforms equivariant baselines in 3D molecule generation tasks, with similar or even less computation. Moreover, with a novel architecture Canon, CanonFlow achieves state-of-the-art performance on the challenging GEOM-DRUG dataset, and the advantage remains large in few-step generation.

MoEEdit: Efficient and Routing-Stable Knowledge Editing for Mixture-of-Experts LLMs

Knowledge editing (KE) enables precise modifications to factual content in large language models (LLMs). Existing KE methods are largely designed for dense architectures, limiting their applicability to the increasingly prevalent sparse Mixture-of-Experts (MoE) models that underpin modern scalable LLMs. Although MoEs offer strong efficiency and capacity scaling, naively adapting dense-model editors is both computationally costly and prone to routing distribution shifts that undermine stability and consistency. To address these challenges, we introduce MoEEdit, the first routing-stable framework for parameter-modifying knowledge editing in MoE LLMs. Our method reparameterizes expert updates via per-expert null-space projections that keep router inputs invariant and thereby suppress routing shifts. The resulting block-structured optimization is solved efficiently with a block coordinate descent (BCD) solver. Experiments show that MoEEdit attains state-of-the-art efficacy and generalization while preserving high specificity and routing stability, with superior compute and memory efficiency. These results establish a robust foundation for scalable, precise knowledge editing in sparse LLMs and underscore the importance of routing-stable interventions.

Accelerated Sequential Flow Matching: A Bayesian Filtering Perspective

Sequential prediction from streaming observations is a fundamental problem in stochastic dynamical systems, where inherent uncertainty often leads to multiple plausible futures. While diffusion and flow-matching models are capable of modeling complex, multi-modal trajectories, their deployment in real-time streaming environments typically relies on repeated sampling from a non-informative initial distribution, incurring substantial inference latency and potential system backlogs. In this work, we introduce Sequential Flow Matching, a principled framework grounded in Bayesian filtering. By treating streaming inference as learning a probability flow that transports the predictive distribution from one time step to the next, our approach naturally aligns with the recursive structure of Bayesian belief updates. We provide theoretical justification that initializing generation from the previous posterior offers a principled warm start that can accelerate sampling compared to naïve re-sampling. Across a wide range of forecasting, decision-making and state estimation tasks, our method achieves performance competitive with full-step diffusion while requiring only one or very few sampling steps, therefore with faster sampling. It suggests that framing sequential inference via Bayesian filtering provides a new and principled perspective towards efficient real-time deployment of flow-based models.

Scalable Spatio-Temporal SE(3) Diffusion for Long-Horizon Protein Dynamics

Molecular dynamics (MD) simulations remain the gold standard for studying protein dynamics, but their computational cost limits access to biologically relevant timescales. Recent generative models have shown promise in accelerating simulations, yet they struggle with long-horizon generation due to architectural constraints, error accumulation, and inadequate modeling of spatio-temporal dynamics. We present STAR-MD (Spatio-Temporal Autoregressive Rollout for Molecular Dynamics), a scalable SE(3)-equivariant diffusion model that generates physically plausible protein trajectories over microsecond timescales. Our key innovation is a causal diffusion transformer with joint spatio-temporal attention that efficiently captures complex space-time dependencies while avoiding the memory bottlenecks of existing methods. On the standard ATLAS benchmark, STAR-MD achieves state-of-the-art performance across all metrics--substantially improving conformational coverage, structural validity, and dynamic fidelity compared to previous methods. STAR-MD successfully extrapolates to generate stable microsecond-scale trajectories where baseline methods fail catastrophically, maintaining high structural quality throughout the extended rollout. Our comprehensive evaluation reveals severe limitations in current models for long-horizon generation, while demonstrating that STAR-MD's joint spatio-temporal modeling enables robust dynamics simulation at biologically relevant timescales, paving the way for accelerated exploration of protein function.

GRIP: Algorithm-Agnostic Machine Unlearning for Mixture-of-Experts via Geometric Router Constraints

Machine unlearning (MU) for large language models has become critical for AI safety, yet existing methods fail to generalize to Mixture-of-Experts (MoE) architectures. We identify that traditional unlearning methods exploit MoE's architectural vulnerability: they manipulate routers to redirect queries away from knowledgeable experts rather than erasing knowledge, causing a loss of model utility and superficial forgetting. We propose Geometric Routing Invariance Preservation (GRIP), an algorithm-agnostic framework for unlearning for MoE. Our core contribution is a geometric constraint, implemented by projecting router gradient updates into an expert-specific null-space. Crucially, this decouples routing stability from parameter rigidity: while discrete expert selections remain stable for retained knowledge, the continuous router parameters remain plastic within the null space, allowing the model to undergo necessary internal reconfiguration to satisfy unlearning objectives. This forces the unlearning optimization to erase knowledge directly from expert parameters rather than exploiting the superficial router manipulation shortcut. GRIP functions as an adapter, constraining router parameter updates without modifying the underlying unlearning algorithm. Extensive experiments on large-scale MoE models demonstrate that our adapter eliminates expert selection shift (achieving over 95% routing stability) across all tested unlearning methods while preserving their utility. By preventing existing algorithms from exploiting MoE model's router vulnerability, GRIP adapts existing unlearning research from dense architectures to MoEs.

Rethinking the Value of Multi-Agent Workflow: A Strong Single Agent Baseline

Recent advances in LLM-based multi-agent systems (MAS) show that workflows composed of multiple LLM agents with distinct roles, tools, and communication patterns can outperform single-LLM baselines on complex tasks. However, most frameworks are homogeneous, where all agents share the same base LLM and differ only in prompts, tools, and positions in the workflow. This raises the question of whether such workflows can be simulated by a single agent through multi-turn conversations. We investigate this across seven benchmarks spanning coding, mathematics, general question answering, domain-specific reasoning, and real-world planning and tool use. Our results show that a single agent can reach the performance of homogeneous workflows with an efficiency advantage from KV cache reuse, and can even match the performance of an automatically optimized heterogeneous workflow. Building on this finding, we propose \textbf{OneFlow}, an algorithm that automatically tailors workflows for single-agent execution, reducing inference costs compared to existing automatic multi-agent design frameworks without trading off accuracy. These results position the single-LLM implementation of multi-agent workflows as a strong baseline for MAS research. We also note that single-LLM methods cannot capture heterogeneous workflows due to the lack of KV cache sharing across different LLMs, highlighting future opportunities in developing \textit{truly} heterogeneous multi-agent systems.

Step-DeepResearch Technical Report

As LLMs shift toward autonomous agents, Deep Research has emerged as a pivotal metric. However, existing academic benchmarks like BrowseComp often fail to meet real-world demands for open-ended research, which requires robust skills in intent recognition, long-horizon decision-making, and cross-source verification. To address this, we introduce Step-DeepResearch, a cost-effective, end-to-end agent. We propose a Data Synthesis Strategy Based on Atomic Capabilities to reinforce planning and report writing, combined with a progressive training path from agentic mid-training to SFT and RL. Enhanced by a Checklist-style Judger, this approach significantly improves robustness. Furthermore, to bridge the evaluation gap in the Chinese domain, we establish ADR-Bench for realistic deep research scenarios. Experimental results show that Step-DeepResearch (32B) scores 61.4% on Scale AI Research Rubrics. On ADR-Bench, it significantly outperforms comparable models and rivals SOTA closed-source models like OpenAI and Gemini DeepResearch. These findings prove that refined training enables medium-sized models to achieve expert-level capabilities at industry-leading cost-efficiency.

Simultaneous Secrecy and Covert Communications (SSACC) in Mobility-Aware RIS-Aided Networks

In this paper, we propose a simultaneous secrecy and covert communications (SSACC) scheme in a reconfigurable intelligent surface (RIS)-aided network with a cooperative jammer. The scheme enhances communication security by maximizing the secrecy capacity and the detection error probability (DEP). Under a worst-case scenario for covert communications, we consider that the eavesdropper can optimally adjust the detection threshold to minimize the DEP. Accordingly, we derive closedform expressions for both average minimum DEP (AMDEP) and average secrecy capacity (ASC). To balance AMDEP and ASC, we propose a new performance metric and design an algorithm based on generative diffusion models (GDM) and deep reinforcement learning (DRL). The algorithm maximizes data rates under user mobility while ensuring high AMDEP and ASC by optimizing power allocation. Simulation results demonstrate that the proposed algorithm achieves faster convergence and superior performance compared to conventional deep deterministic policy gradient (DDPG) methods, thereby validating its effectiveness in balancing security and capacity performance.

CoDA: A Context-Decoupled Hierarchical Agent with Reinforcement Learning

Large Language Model (LLM) agents trained with reinforcement learning (RL) show great promise for solving complex, multi-step tasks. However, their performance is often crippled by "Context Explosion", where the accumulation of long text outputs overwhelms the model's context window and leads to reasoning failures. To address this, we introduce CoDA, a Context-Decoupled hierarchical Agent, a simple but effective reinforcement learning framework that decouples high-level planning from low-level execution. It employs a single, shared LLM backbone that learns to operate in two distinct, contextually isolated roles: a high-level Planner that decomposes tasks within a concise strategic context, and a low-level Executor that handles tool interactions in an ephemeral, isolated workspace. We train this unified agent end-to-end using PECO (Planner-Executor Co-Optimization), a reinforcement learning methodology that applies a trajectory-level reward to jointly optimize both roles, fostering seamless collaboration through context-dependent policy updates. Extensive experiments demonstrate that CoDA achieves significant performance improvements over state-of-the-art baselines on complex multi-hop question-answering benchmarks, and it exhibits strong robustness in long-context scenarios, maintaining stable performance while all other baselines suffer severe degradation, thus further validating the effectiveness of our hierarchical design in mitigating context overload.

From Small to Large: Generalization Bounds for Transformers on Variable-Size Inputs

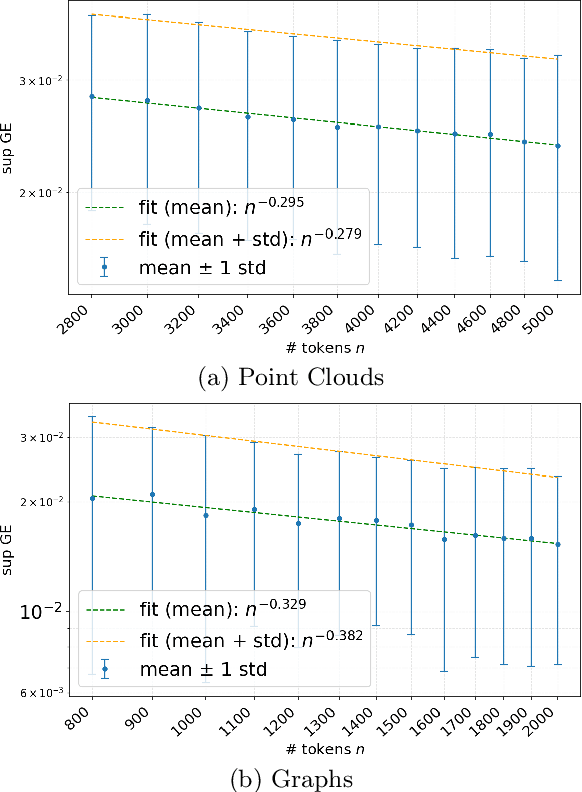
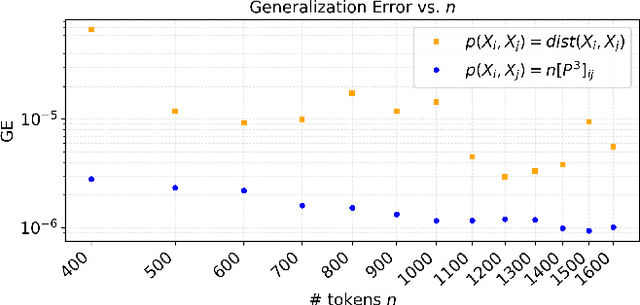
Transformers exhibit a notable property of \emph{size generalization}, demonstrating an ability to extrapolate from smaller token sets to significantly longer ones. This behavior has been documented across diverse applications, including point clouds, graphs, and natural language. Despite its empirical success, this capability still lacks some rigorous theoretical characterizations. In this paper, we develop a theoretical framework to analyze this phenomenon for geometric data, which we represent as discrete samples from a continuous source (e.g., point clouds from manifolds, graphs from graphons). Our core contribution is a bound on the error between the Transformer's output for a discrete sample and its continuous-domain equivalent. We prove that for Transformers with stable positional encodings, this bound is determined by the sampling density and the intrinsic dimensionality of the data manifold. Experiments on graphs and point clouds of various sizes confirm the tightness of our theoretical bound.