On the Query Complexity of Verifier-Assisted Language Generation

Recently, a plethora of works have proposed inference-time algorithms (e.g. best-of-n), which incorporate verifiers to assist the generation process. Their quality-efficiency trade-offs have been empirically benchmarked on a variety of constrained generation tasks, but the algorithmic design landscape is still largely poorly understood. In this paper, we develop a mathematical framework for reasoning about constrained generation using a pre-trained language model generator oracle and a process verifier--which can decide whether a prefix can be extended to a string which satisfies the constraints of choice. We show that even in very simple settings, access to a verifier can render an intractable problem (information-theoretically or computationally) to a tractable one. In fact, we show even simple algorithms, like tokenwise rejection sampling, can enjoy significant benefits from access to a verifier. Empirically, we show that a natural modification of tokenwise rejection sampling, in which the sampler is allowed to "backtrack" (i.e., erase the final few generated tokens) has robust and substantive benefits over natural baselines (e.g. (blockwise) rejection sampling, nucleus sampling)--both in terms of computational efficiency, accuracy and diversity.

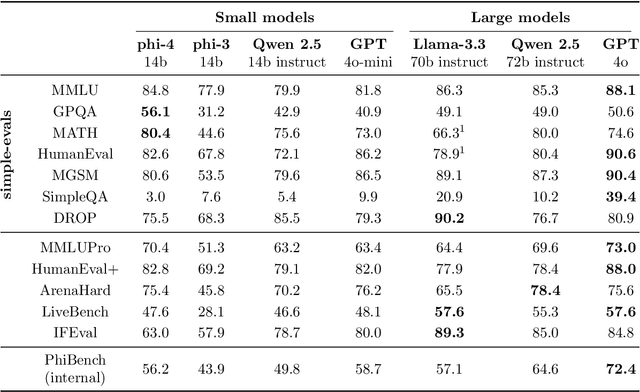
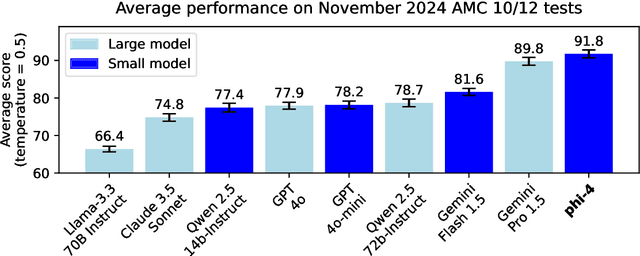
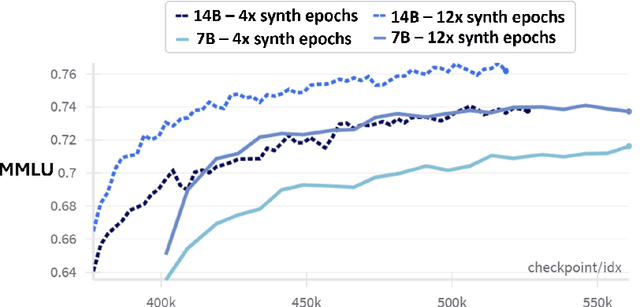
Phi-4 Technical Report

We present phi-4, a 14-billion parameter language model developed with a training recipe that is centrally focused on data quality. Unlike most language models, where pre-training is based primarily on organic data sources such as web content or code, phi-4 strategically incorporates synthetic data throughout the training process. While previous models in the Phi family largely distill the capabilities of a teacher model (specifically GPT-4), phi-4 substantially surpasses its teacher model on STEM-focused QA capabilities, giving evidence that our data-generation and post-training techniques go beyond distillation. Despite minimal changes to the phi-3 architecture, phi-4 achieves strong performance relative to its size -- especially on reasoning-focused benchmarks -- due to improved data, training curriculum, and innovations in the post-training scheme.

Self-Improvement in Language Models: The Sharpening Mechanism

Recent work in language modeling has raised the possibility of self-improvement, where a language models evaluates and refines its own generations to achieve higher performance without external feedback. It is impossible for this self-improvement to create information that is not already in the model, so why should we expect that this will lead to improved capabilities? We offer a new perspective on the capabilities of self-improvement through a lens we refer to as sharpening. Motivated by the observation that language models are often better at verifying response quality than they are at generating correct responses, we formalize self-improvement as using the model itself as a verifier during post-training in order to ``sharpen'' the model to one placing large mass on high-quality sequences, thereby amortizing the expensive inference-time computation of generating good sequences. We begin by introducing a new statistical framework for sharpening in which the learner aims to sharpen a pre-trained base policy via sample access, and establish fundamental limits. Then we analyze two natural families of self-improvement algorithms based on SFT and RLHF.

ASL STEM Wiki: Dataset and Benchmark for Interpreting STEM Articles

Deaf and hard-of-hearing (DHH) students face significant barriers in accessing science, technology, engineering, and mathematics (STEM) education, notably due to the scarcity of STEM resources in signed languages. To help address this, we introduce ASL STEM Wiki: a parallel corpus of 254 Wikipedia articles on STEM topics in English, interpreted into over 300 hours of American Sign Language (ASL). ASL STEM Wiki is the first continuous signing dataset focused on STEM, facilitating the development of AI resources for STEM education in ASL. We identify several use cases of ASL STEM Wiki with human-centered applications. For example, because this dataset highlights the frequent use of fingerspelling for technical concepts, which inhibits DHH students' ability to learn, we develop models to identify fingerspelled words -- which can later be used to query for appropriate ASL signs to suggest to interpreters.

Phi-3 Technical Report: A Highly Capable Language Model Locally on Your Phone

We introduce phi-3-mini, a 3.8 billion parameter language model trained on 3.3 trillion tokens, whose overall performance, as measured by both academic benchmarks and internal testing, rivals that of models such as Mixtral 8x7B and GPT-3.5 (e.g., phi-3-mini achieves 69% on MMLU and 8.38 on MT-bench), despite being small enough to be deployed on a phone. The innovation lies entirely in our dataset for training, a scaled-up version of the one used for phi-2, composed of heavily filtered web data and synthetic data. The model is also further aligned for robustness, safety, and chat format. We also provide some initial parameter-scaling results with a 7B and 14B models trained for 4.8T tokens, called phi-3-small and phi-3-medium, both significantly more capable than phi-3-mini (e.g., respectively 75% and 78% on MMLU, and 8.7 and 8.9 on MT-bench).

Can large language models explore in-context?

We investigate the extent to which contemporary Large Language Models (LLMs) can engage in exploration, a core capability in reinforcement learning and decision making. We focus on native performance of existing LLMs, without training interventions. We deploy LLMs as agents in simple multi-armed bandit environments, specifying the environment description and interaction history entirely in-context, i.e., within the LLM prompt. We experiment with GPT-3.5, GPT-4, and Llama2, using a variety of prompt designs, and find that the models do not robustly engage in exploration without substantial interventions: i) Across all of our experiments, only one configuration resulted in satisfactory exploratory behavior: GPT-4 with chain-of-thought reasoning and an externally summarized interaction history, presented as sufficient statistics; ii) All other configurations did not result in robust exploratory behavior, including those with chain-of-thought reasoning but unsummarized history. Although these findings can be interpreted positively, they suggest that external summarization -- which may not be possible in more complex settings -- is important for obtaining desirable behavior from LLM agents. We conclude that non-trivial algorithmic interventions, such as fine-tuning or dataset curation, may be required to empower LLM-based decision making agents in complex settings.

Butterfly Effects of SGD Noise: Error Amplification in Behavior Cloning and Autoregression

This work studies training instabilities of behavior cloning with deep neural networks. We observe that minibatch SGD updates to the policy network during training result in sharp oscillations in long-horizon rewards, despite negligibly affecting the behavior cloning loss. We empirically disentangle the statistical and computational causes of these oscillations, and find them to stem from the chaotic propagation of minibatch SGD noise through unstable closed-loop dynamics. While SGD noise is benign in the single-step action prediction objective, it results in catastrophic error accumulation over long horizons, an effect we term gradient variance amplification (GVA). We show that many standard mitigation techniques do not alleviate GVA, but find an exponential moving average (EMA) of iterates to be surprisingly effective at doing so. We illustrate the generality of this phenomenon by showing the existence of GVA and its amelioration by EMA in both continuous control and autoregressive language generation. Finally, we provide theoretical vignettes that highlight the benefits of EMA in alleviating GVA and shed light on the extent to which classical convex models can help in understanding the benefits of iterate averaging in deep learning.

Pareto Frontiers in Neural Feature Learning: Data, Compute, Width, and Luck

This work investigates the nuanced algorithm design choices for deep learning in the presence of computational-statistical gaps. We begin by considering offline sparse parity learning, a supervised classification problem which admits a statistical query lower bound for gradient-based training of a multilayer perceptron. This lower bound can be interpreted as a multi-resource tradeoff frontier: successful learning can only occur if one is sufficiently rich (large model), knowledgeable (large dataset), patient (many training iterations), or lucky (many random guesses). We show, theoretically and experimentally, that sparse initialization and increasing network width yield significant improvements in sample efficiency in this setting. Here, width plays the role of parallel search: it amplifies the probability of finding "lottery ticket" neurons, which learn sparse features more sample-efficiently. Finally, we show that the synthetic sparse parity task can be useful as a proxy for real problems requiring axis-aligned feature learning. We demonstrate improved sample efficiency on tabular classification benchmarks by using wide, sparsely-initialized MLP models; these networks sometimes outperform tuned random forests.

Exposing Attention Glitches with Flip-Flop Language Modeling

Why do large language models sometimes output factual inaccuracies and exhibit erroneous reasoning? The brittleness of these models, particularly when executing long chains of reasoning, currently seems to be an inevitable price to pay for their advanced capabilities of coherently synthesizing knowledge, pragmatics, and abstract thought. Towards making sense of this fundamentally unsolved problem, this work identifies and analyzes the phenomenon of attention glitches, in which the Transformer architecture's inductive biases intermittently fail to capture robust reasoning. To isolate the issue, we introduce flip-flop language modeling (FFLM), a parametric family of synthetic benchmarks designed to probe the extrapolative behavior of neural language models. This simple generative task requires a model to copy binary symbols over long-range dependencies, ignoring the tokens in between. We find that Transformer FFLMs suffer from a long tail of sporadic reasoning errors, some of which we can eliminate using various regularization techniques. Our preliminary mechanistic analyses show why the remaining errors may be very difficult to diagnose and resolve. We hypothesize that attention glitches account for (some of) the closed-domain hallucinations in natural LLMs.

Learning Hidden Markov Models Using Conditional Samples

This paper is concerned with the computational complexity of learning the Hidden Markov Model (HMM). Although HMMs are some of the most widely used tools in sequential and time series modeling, they are cryptographically hard to learn in the standard setting where one has access to i.i.d. samples of observation sequences. In this paper, we depart from this setup and consider an interactive access model, in which the algorithm can query for samples from the conditional distributions of the HMMs. We show that interactive access to the HMM enables computationally efficient learning algorithms, thereby bypassing cryptographic hardness. Specifically, we obtain efficient algorithms for learning HMMs in two settings: (a) An easier setting where we have query access to the exact conditional probabilities. Here our algorithm runs in polynomial time and makes polynomially many queries to approximate any HMM in total variation distance. (b) A harder setting where we can only obtain samples from the conditional distributions. Here the performance of the algorithm depends on a new parameter, called the fidelity of the HMM. We show that this captures cryptographically hard instances and previously known positive results. We also show that these results extend to a broader class of distributions with latent low rank structure. Our algorithms can be viewed as generalizations and robustifications of Angluin's $L^*$ algorithm for learning deterministic finite automata from membership queries.