Transcendence: Generative Models Can Outperform The Experts That Train Them

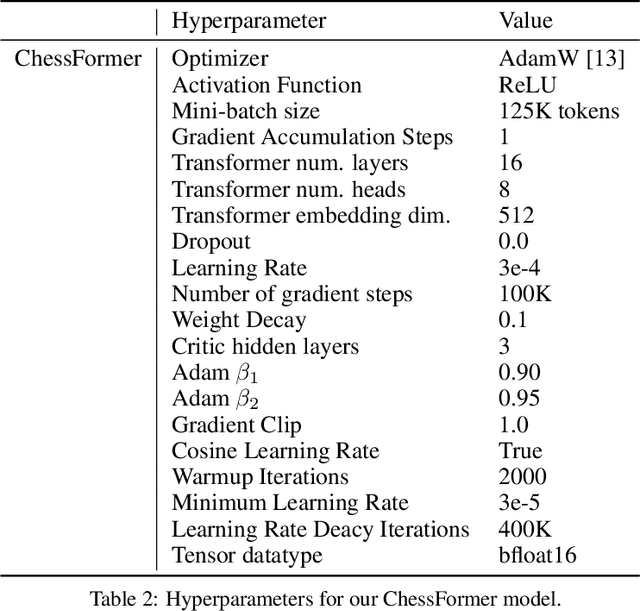
Generative models are trained with the simple objective of imitating the conditional probability distribution induced by the data they are trained on. Therefore, when trained on data generated by humans, we may not expect the artificial model to outperform the humans on their original objectives. In this work, we study the phenomenon of transcendence: when a generative model achieves capabilities that surpass the abilities of the experts generating its data. We demonstrate transcendence by training an autoregressive transformer to play chess from game transcripts, and show that the trained model can sometimes achieve better performance than all players in the dataset. We theoretically prove that transcendence is enabled by low-temperature sampling, and rigorously assess this experimentally. Finally, we discuss other sources of transcendence, laying the groundwork for future investigation of this phenomenon in a broader setting.

Foundational Challenges in Assuring Alignment and Safety of Large Language Models

This work identifies 18 foundational challenges in assuring the alignment and safety of large language models (LLMs). These challenges are organized into three different categories: scientific understanding of LLMs, development and deployment methods, and sociotechnical challenges. Based on the identified challenges, we pose $200+$ concrete research questions.

The Evolution of Statistical Induction Heads: In-Context Learning Markov Chains

Large language models have the ability to generate text that mimics patterns in their inputs. We introduce a simple Markov Chain sequence modeling task in order to study how this in-context learning (ICL) capability emerges. In our setting, each example is sampled from a Markov chain drawn from a prior distribution over Markov chains. Transformers trained on this task form \emph{statistical induction heads} which compute accurate next-token probabilities given the bigram statistics of the context. During the course of training, models pass through multiple phases: after an initial stage in which predictions are uniform, they learn to sub-optimally predict using in-context single-token statistics (unigrams); then, there is a rapid phase transition to the correct in-context bigram solution. We conduct an empirical and theoretical investigation of this multi-phase process, showing how successful learning results from the interaction between the transformer's layers, and uncovering evidence that the presence of the simpler unigram solution may delay formation of the final bigram solution. We examine how learning is affected by varying the prior distribution over Markov chains, and consider the generalization of our in-context learning of Markov chains (ICL-MC) task to $n$-grams for $n > 2$.

Distinguishing the Knowable from the Unknowable with Language Models

We study the feasibility of identifying epistemic uncertainty (reflecting a lack of knowledge), as opposed to aleatoric uncertainty (reflecting entropy in the underlying distribution), in the outputs of large language models (LLMs) over free-form text. In the absence of ground-truth probabilities, we explore a setting where, in order to (approximately) disentangle a given LLM's uncertainty, a significantly larger model stands in as a proxy for the ground truth. We show that small linear probes trained on the embeddings of frozen, pretrained models accurately predict when larger models will be more confident at the token level and that probes trained on one text domain generalize to others. Going further, we propose a fully unsupervised method that achieves non-trivial accuracy on the same task. Taken together, we interpret these results as evidence that LLMs naturally contain internal representations of different types of uncertainty that could potentially be leveraged to devise more informative indicators of model confidence in diverse practical settings.

Watermarks in the Sand: Impossibility of Strong Watermarking for Generative Models

Watermarking generative models consists of planting a statistical signal (watermark) in a model's output so that it can be later verified that the output was generated by the given model. A strong watermarking scheme satisfies the property that a computationally bounded attacker cannot erase the watermark without causing significant quality degradation. In this paper, we study the (im)possibility of strong watermarking schemes. We prove that, under well-specified and natural assumptions, strong watermarking is impossible to achieve. This holds even in the private detection algorithm setting, where the watermark insertion and detection algorithms share a secret key, unknown to the attacker. To prove this result, we introduce a generic efficient watermark attack; the attacker is not required to know the private key of the scheme or even which scheme is used. Our attack is based on two assumptions: (1) The attacker has access to a "quality oracle" that can evaluate whether a candidate output is a high-quality response to a prompt, and (2) The attacker has access to a "perturbation oracle" which can modify an output with a nontrivial probability of maintaining quality, and which induces an efficiently mixing random walk on high-quality outputs. We argue that both assumptions can be satisfied in practice by an attacker with weaker computational capabilities than the watermarked model itself, to which the attacker has only black-box access. Furthermore, our assumptions will likely only be easier to satisfy over time as models grow in capabilities and modalities. We demonstrate the feasibility of our attack by instantiating it to attack three existing watermarking schemes for large language models: Kirchenbauer et al. (2023), Kuditipudi et al. (2023), and Zhao et al. (2023). The same attack successfully removes the watermarks planted by all three schemes, with only minor quality degradation.

Feature emergence via margin maximization: case studies in algebraic tasks

Understanding the internal representations learned by neural networks is a cornerstone challenge in the science of machine learning. While there have been significant recent strides in some cases towards understanding how neural networks implement specific target functions, this paper explores a complementary question -- why do networks arrive at particular computational strategies? Our inquiry focuses on the algebraic learning tasks of modular addition, sparse parities, and finite group operations. Our primary theoretical findings analytically characterize the features learned by stylized neural networks for these algebraic tasks. Notably, our main technique demonstrates how the principle of margin maximization alone can be used to fully specify the features learned by the network. Specifically, we prove that the trained networks utilize Fourier features to perform modular addition and employ features corresponding to irreducible group-theoretic representations to perform compositions in general groups, aligning closely with the empirical observations of Nanda et al. and Chughtai et al. More generally, we hope our techniques can help to foster a deeper understanding of why neural networks adopt specific computational strategies.

Pareto Frontiers in Neural Feature Learning: Data, Compute, Width, and Luck

This work investigates the nuanced algorithm design choices for deep learning in the presence of computational-statistical gaps. We begin by considering offline sparse parity learning, a supervised classification problem which admits a statistical query lower bound for gradient-based training of a multilayer perceptron. This lower bound can be interpreted as a multi-resource tradeoff frontier: successful learning can only occur if one is sufficiently rich (large model), knowledgeable (large dataset), patient (many training iterations), or lucky (many random guesses). We show, theoretically and experimentally, that sparse initialization and increasing network width yield significant improvements in sample efficiency in this setting. Here, width plays the role of parallel search: it amplifies the probability of finding "lottery ticket" neurons, which learn sparse features more sample-efficiently. Finally, we show that the synthetic sparse parity task can be useful as a proxy for real problems requiring axis-aligned feature learning. We demonstrate improved sample efficiency on tabular classification benchmarks by using wide, sparsely-initialized MLP models; these networks sometimes outperform tuned random forests.

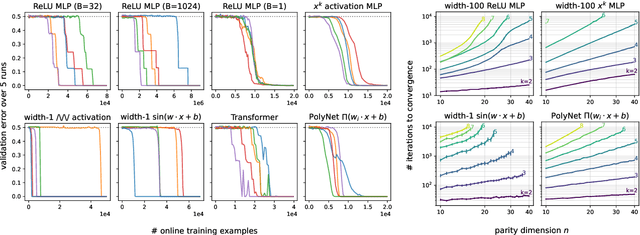
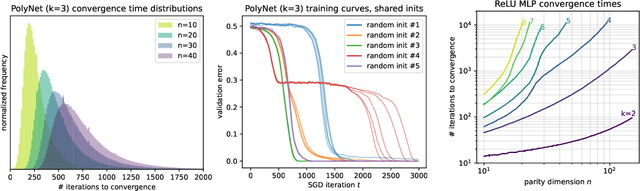
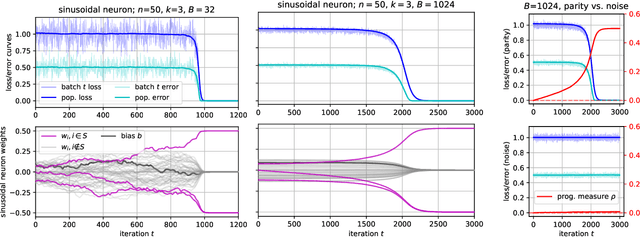
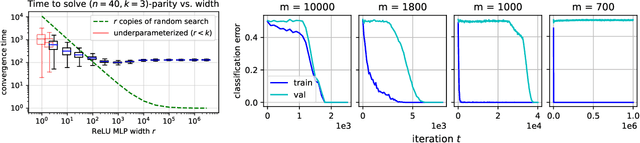
Hidden Progress in Deep Learning: SGD Learns Parities Near the Computational Limit

There is mounting empirical evidence of emergent phenomena in the capabilities of deep learning methods as we scale up datasets, model sizes, and training times. While there are some accounts of how these resources modulate statistical capacity, far less is known about their effect on the computational problem of model training. This work conducts such an exploration through the lens of learning $k$-sparse parities of $n$ bits, a canonical family of problems which pose theoretical computational barriers. In this setting, we find that neural networks exhibit surprising phase transitions when scaling up dataset size and running time. In particular, we demonstrate empirically that with standard training, a variety of architectures learn sparse parities with $n^{O(k)}$ examples, with loss (and error) curves abruptly dropping after $n^{O(k)}$ iterations. These positive results nearly match known SQ lower bounds, even without an explicit sparsity-promoting prior. We elucidate the mechanisms of these phenomena with a theoretical analysis: we find that the phase transition in performance is not due to SGD "stumbling in the dark" until it finds the hidden set of features (a natural algorithm which also runs in $n^{O(k)}$ time); instead, we show that SGD gradually amplifies a Fourier gap in the population gradient.

Inductive Biases and Variable Creation in Self-Attention Mechanisms

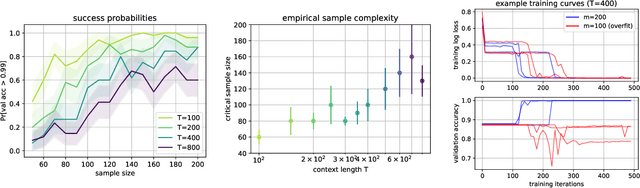
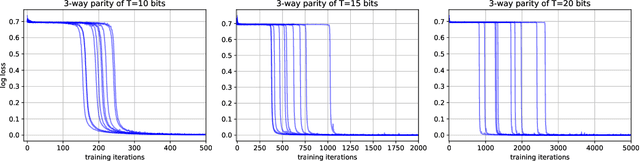
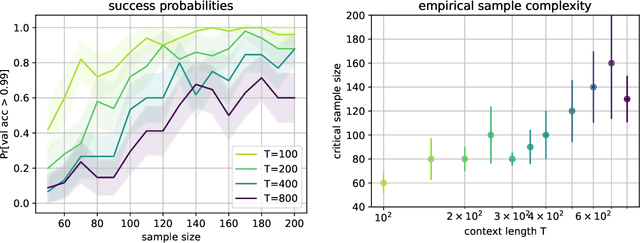
Self-attention, an architectural motif designed to model long-range interactions in sequential data, has driven numerous recent breakthroughs in natural language processing and beyond. This work provides a theoretical analysis of the inductive biases of self-attention modules, where our focus is to rigorously establish which functions and long-range dependencies self-attention blocks prefer to represent. Our main result shows that bounded-norm Transformer layers create sparse variables: they can represent sparse functions of the input sequence, with sample complexity scaling only logarithmically with the context length. Furthermore, we propose new experimental protocols to support this analysis and to guide the practice of training Transformers, built around the large body of work on provably learning sparse Boolean functions.

SGD on Neural Networks Learns Functions of Increasing Complexity

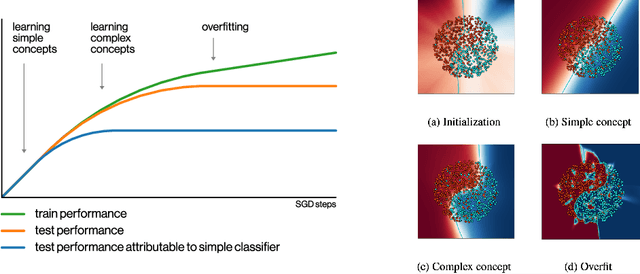
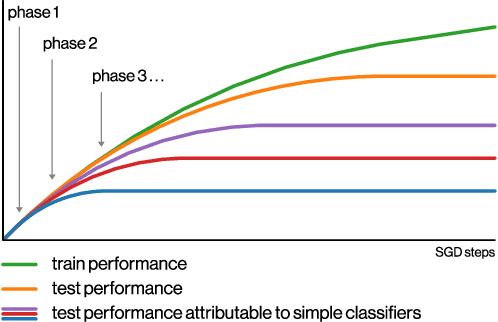
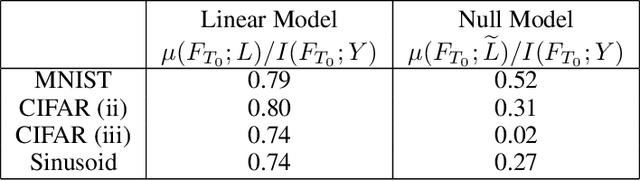
We perform an experimental study of the dynamics of Stochastic Gradient Descent (SGD) in learning deep neural networks for several real and synthetic classification tasks. We show that in the initial epochs, almost all of the performance improvement of the classifier obtained by SGD can be explained by a linear classifier. More generally, we give evidence for the hypothesis that, as iterations progress, SGD learns functions of increasing complexity. This hypothesis can be helpful in explaining why SGD-learned classifiers tend to generalize well even in the over-parameterized regime. We also show that the linear classifier learned in the initial stages is "retained" throughout the execution even if training is continued to the point of zero training error, and complement this with a theoretical result in a simplified model. Key to our work is a new measure of how well one classifier explains the performance of another, based on conditional mutual information.