Multi-Task Imitation Learning for Linear Dynamical Systems

We study representation learning for efficient imitation learning over linear systems. In particular, we consider a setting where learning is split into two phases: (a) a pre-training step where a shared $k$-dimensional representation is learned from $H$ source policies, and (b) a target policy fine-tuning step where the learned representation is used to parameterize the policy class. We find that the imitation gap over trajectories generated by the learned target policy is bounded by $\tilde{O}\left( \frac{k n_x}{HN_{\mathrm{shared}}} + \frac{k n_u}{N_{\mathrm{target}}}\right)$, where $n_x > k$ is the state dimension, $n_u$ is the input dimension, $N_{\mathrm{shared}}$ denotes the total amount of data collected for each policy during representation learning, and $N_{\mathrm{target}}$ is the amount of target task data. This result formalizes the intuition that aggregating data across related tasks to learn a representation can significantly improve the sample efficiency of learning a target task. The trends suggested by this bound are corroborated in simulation.

Lyapunov Density Models: Constraining Distribution Shift in Learning-Based Control

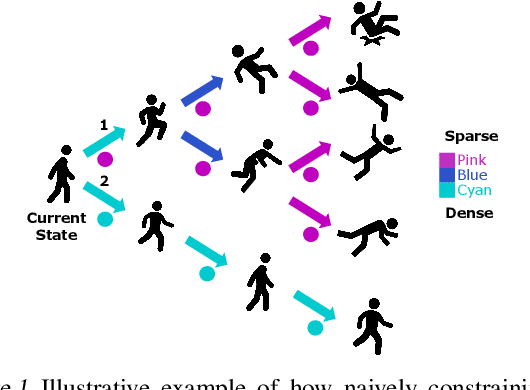
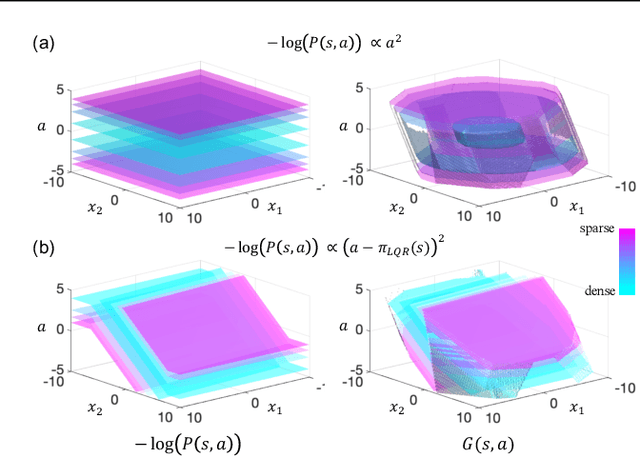
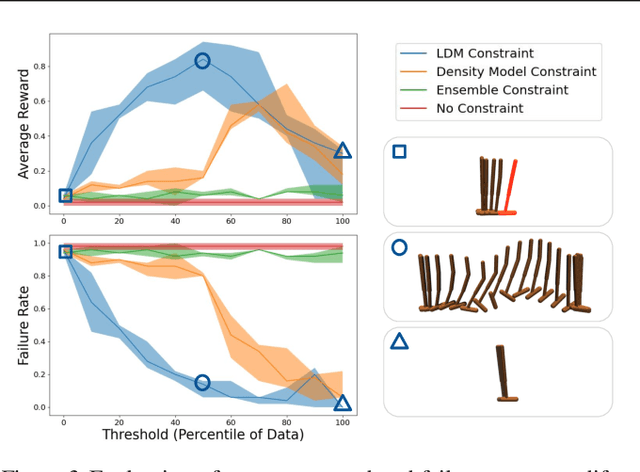
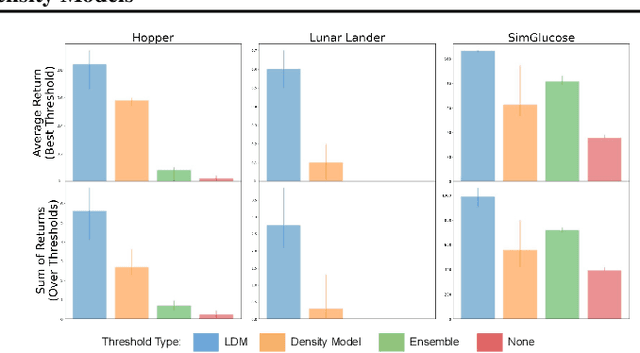
Learned models and policies can generalize effectively when evaluated within the distribution of the training data, but can produce unpredictable and erroneous outputs on out-of-distribution inputs. In order to avoid distribution shift when deploying learning-based control algorithms, we seek a mechanism to constrain the agent to states and actions that resemble those that it was trained on. In control theory, Lyapunov stability and control-invariant sets allow us to make guarantees about controllers that stabilize the system around specific states, while in machine learning, density models allow us to estimate the training data distribution. Can we combine these two concepts, producing learning-based control algorithms that constrain the system to in-distribution states using only in-distribution actions? In this work, we propose to do this by combining concepts from Lyapunov stability and density estimation, introducing Lyapunov density models: a generalization of control Lyapunov functions and density models that provides guarantees on an agent's ability to stay in-distribution over its entire trajectory.

Inducing Structure in Reward Learning by Learning Features

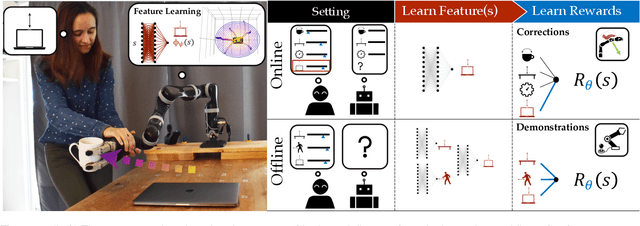
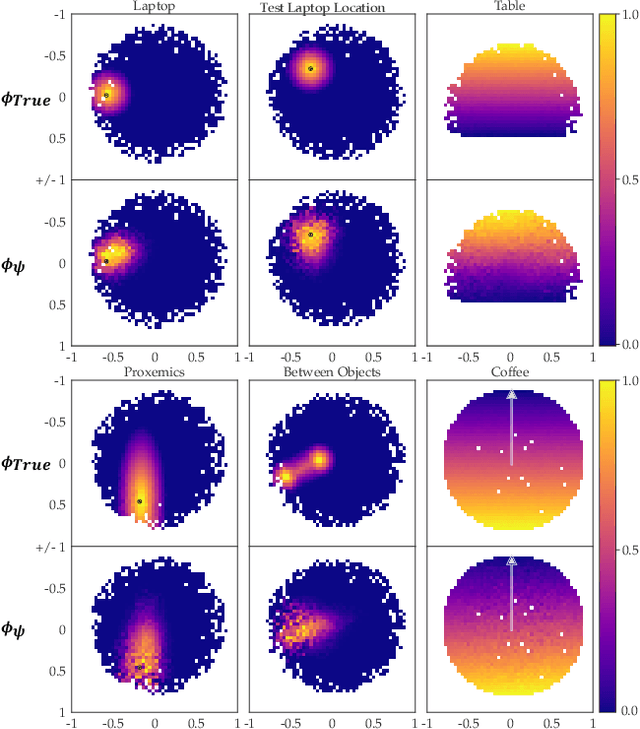
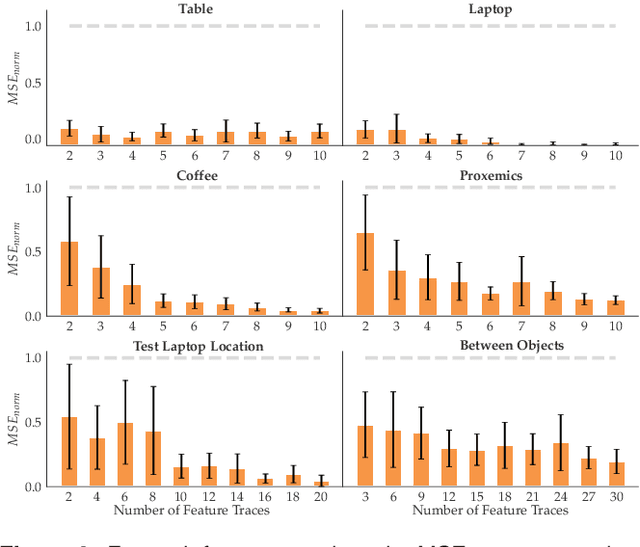
Reward learning enables robots to learn adaptable behaviors from human input. Traditional methods model the reward as a linear function of hand-crafted features, but that requires specifying all the relevant features a priori, which is impossible for real-world tasks. To get around this issue, recent deep Inverse Reinforcement Learning (IRL) methods learn rewards directly from the raw state but this is challenging because the robot has to implicitly learn the features that are important and how to combine them, simultaneously. Instead, we propose a divide and conquer approach: focus human input specifically on learning the features separately, and only then learn how to combine them into a reward. We introduce a novel type of human input for teaching features and an algorithm that utilizes it to learn complex features from the raw state space. The robot can then learn how to combine them into a reward using demonstrations, corrections, or other reward learning frameworks. We demonstrate our method in settings where all features have to be learned from scratch, as well as where some of the features are known. By first focusing human input specifically on the feature(s), our method decreases sample complexity and improves generalization of the learned reward over a deepIRL baseline. We show this in experiments with a physical 7DOF robot manipulator, as well as in a user study conducted in a simulated environment.

Learning from learning machines: a new generation of AI technology to meet the needs of science

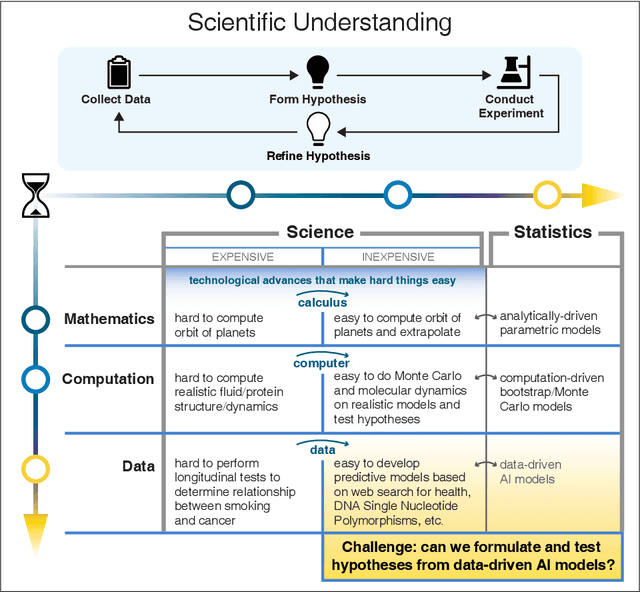
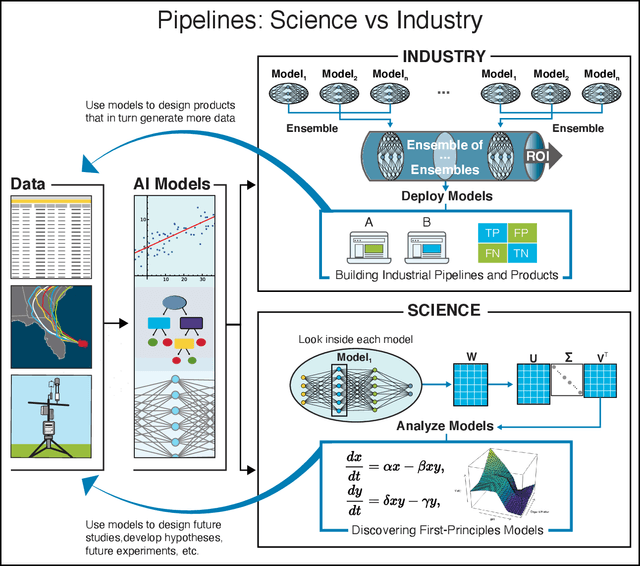
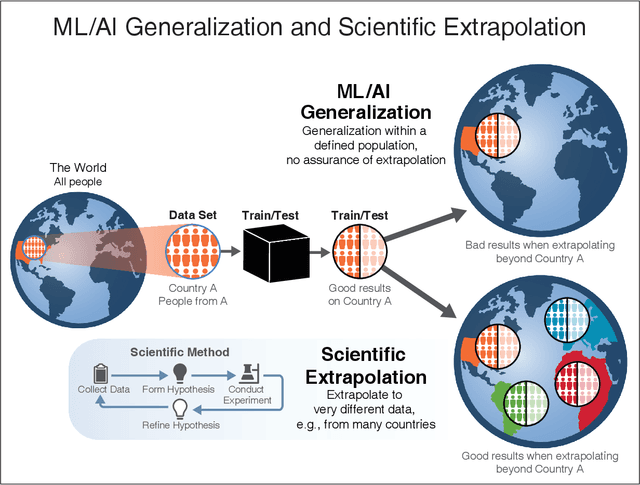
We outline emerging opportunities and challenges to enhance the utility of AI for scientific discovery. The distinct goals of AI for industry versus the goals of AI for science create tension between identifying patterns in data versus discovering patterns in the world from data. If we address the fundamental challenges associated with "bridging the gap" between domain-driven scientific models and data-driven AI learning machines, then we expect that these AI models can transform hypothesis generation, scientific discovery, and the scientific process itself.

Incorporating Data Uncertainty in Object Tracking Algorithms

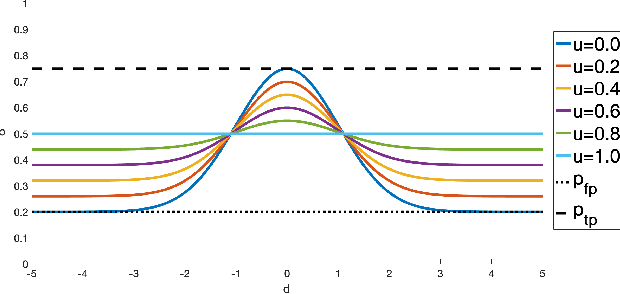
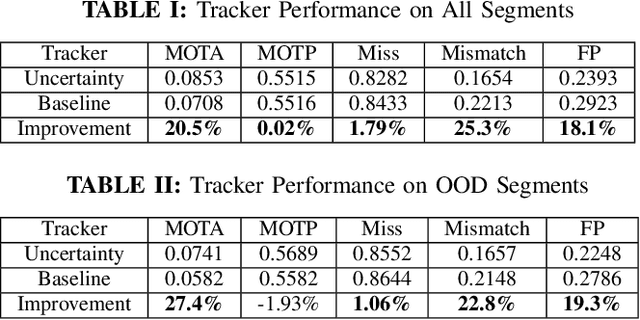
Methodologies for incorporating the uncertainties characteristic of data-driven object detectors into object tracking algorithms are explored. Object tracking methods rely on measurement error models, typically in the form of measurement noise, false positive rates, and missed detection rates. Each of these quantities, in general, can be dependent on object or measurement location. However, for detections generated from neural-network processed camera inputs, these measurement error statistics are not sufficient to represent the primary source of errors, namely a dissimilarity between run-time sensor input and the training data upon which the detector was trained. To this end, we investigate incorporating data uncertainty into object tracking methods such as to improve the ability to track objects, and particularly those which out-of-distribution w.r.t. training data. The proposed methodologies are validated on an object tracking benchmark as well on experiments with a real autonomous aircraft.

Multi-Task Learning with Sequence-Conditioned Transporter Networks

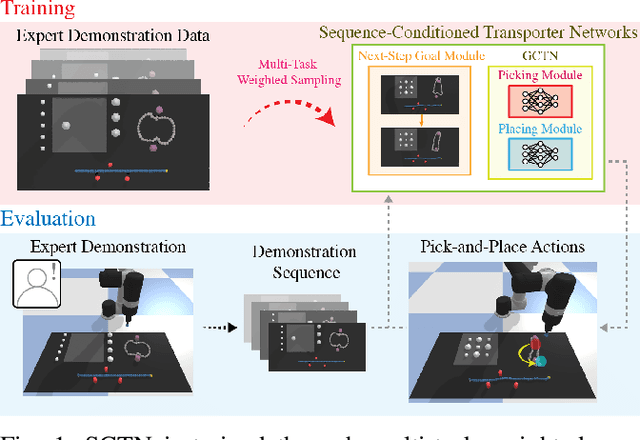
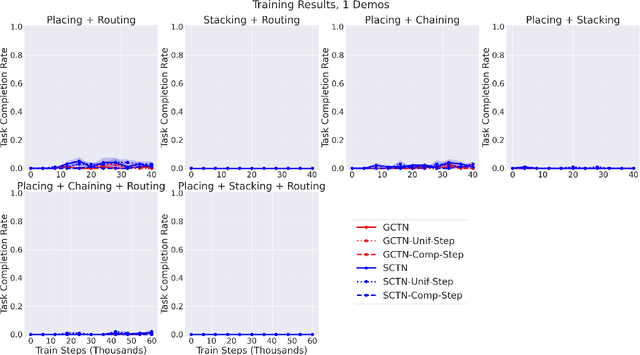
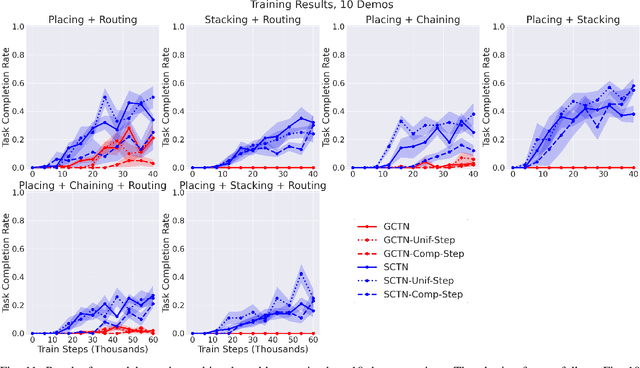
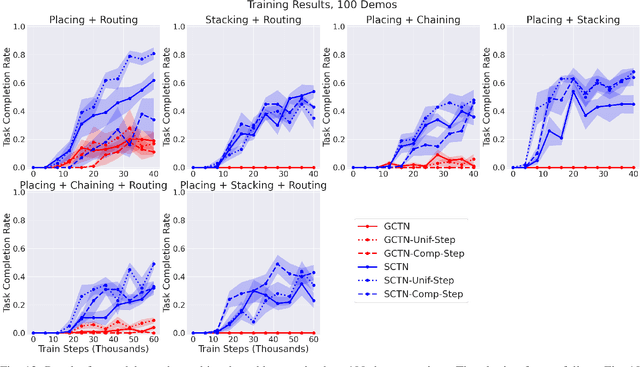
Enabling robots to solve multiple manipulation tasks has a wide range of industrial applications. While learning-based approaches enjoy flexibility and generalizability, scaling these approaches to solve such compositional tasks remains a challenge. In this work, we aim to solve multi-task learning through the lens of sequence-conditioning and weighted sampling. First, we propose a new suite of benchmark specifically aimed at compositional tasks, MultiRavens, which allows defining custom task combinations through task modules that are inspired by industrial tasks and exemplify the difficulties in vision-based learning and planning methods. Second, we propose a vision-based end-to-end system architecture, Sequence-Conditioned Transporter Networks, which augments Goal-Conditioned Transporter Networks with sequence-conditioning and weighted sampling and can efficiently learn to solve multi-task long horizon problems. Our analysis suggests that not only the new framework significantly improves pick-and-place performance on novel 10 multi-task benchmark problems, but also the multi-task learning with weighted sampling can vastly improve learning and agent performances on individual tasks.

The Computation of Approximate Generalized Feedback Nash Equilibria

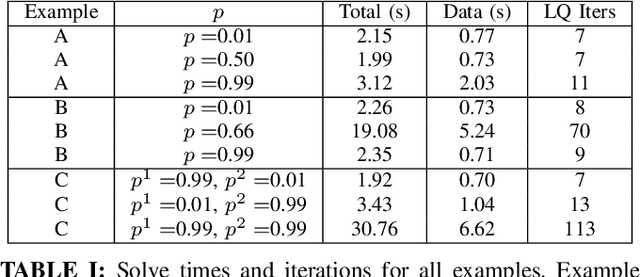
We present the concept of a Generalized Feedback Nash Equilibrium (GFNE) in dynamic games, extending the Feedback Nash Equilibrium concept to games in which players are subject to state and input constraints. We formalize necessary and sufficient conditions for (local) GFNE solutions at the trajectory level, which enable the development of efficient numerical methods for their computation. Specifically, we propose a Newton-style method for finding game trajectories which satisfy the necessary conditions, which can then be checked against the sufficiency conditions. We show that the evaluation of the necessary conditions in general requires computing a series of nested, implicitly-defined derivatives, which quickly becomes intractable. To this end, we introduce an approximation to the necessary conditions which is amenable to efficient evaluation, and in turn, computation of solutions. We term the solutions to the approximate necessary conditions Generalized Feedback Quasi Nash Equilibria (GFQNE), and we introduce numerical methods for their computation. In particular, we develop a Sequential Linear-Quadratic Game approach, in which a locally approximate LQ game is solved at each iteration. The development of this method relies on the ability to compute a GFNE to inequality- and equality-constrained LQ games, and therefore specific methods for the solution of these special cases are developed in detail. We demonstrate the effectiveness of the proposed solution approach on a dynamic game arising in an autonomous driving application.

Multi-Hypothesis Interactions in Game-Theoretic Motion Planning

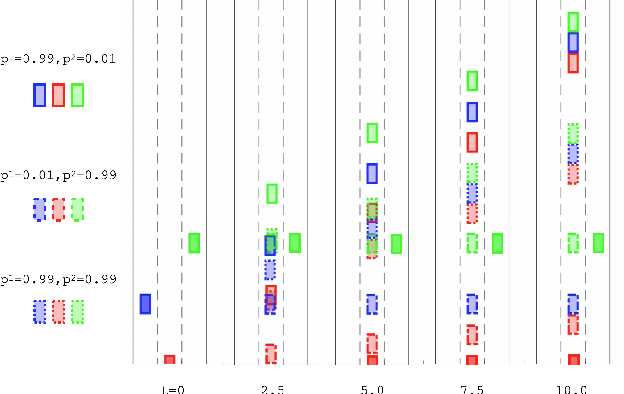
We present a novel method for handling uncertainty about the intentions of non-ego players in dynamic games, with application to motion planning for autonomous vehicles. Equilibria in these games explicitly account for interaction among other agents in the environment, such as drivers and pedestrians. Our method models the uncertainty about the intention of other agents by constructing multiple hypotheses about the objectives and constraints of other agents in the scene. For each candidate hypothesis, we associate a Bernoulli random variable representing the probability of that hypothesis, which may or may not be independent of the probability of other hypotheses. We leverage constraint asymmetries and feedback information patterns to incorporate the probabilities of hypotheses in a natural way. Specifically, increasing the probability associated with a given hypothesis from $0$ to $1$ shifts the responsibility of collision avoidance from the hypothesized agent to the ego agent. This method allows the generation of interactive trajectories for the ego agent, where the level of assertiveness or caution that the ego exhibits is directly related to the easy-to-model uncertainty it maintains about the scene.

Testing for Typicality with Respect to an Ensemble of Learned Distributions

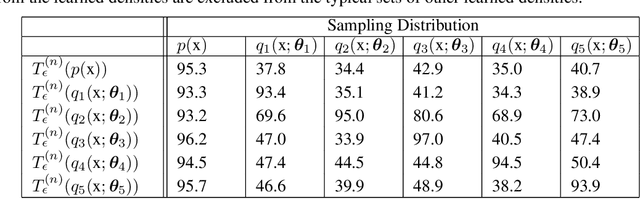
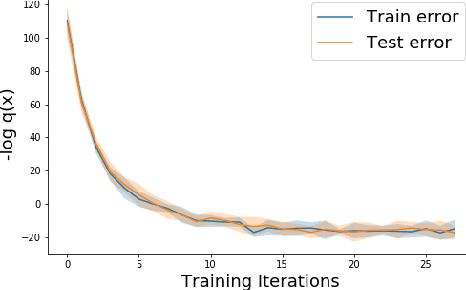
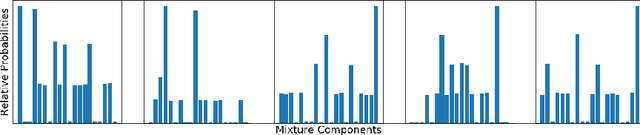
Methods of performing anomaly detection on high-dimensional data sets are needed, since algorithms which are trained on data are only expected to perform well on data that is similar to the training data. There are theoretical results on the ability to detect if a population of data is likely to come from a known base distribution, which is known as the goodness-of-fit problem. One-sample approaches to this problem offer significant computational advantages for online testing, but require knowing a model of the base distribution. The ability to correctly reject anomalous data in this setting hinges on the accuracy of the model of the base distribution. For high dimensional data, learning an accurate-enough model of the base distribution such that anomaly detection works reliably is very challenging, as many researchers have noted in recent years. Existing methods for the one-sample goodness-of-fit problem do not account for the fact that a model of the base distribution is learned. To address that gap, we offer a theoretically motivated approach to account for the density learning procedure. In particular, we propose training an ensemble of density models, considering data to be anomalous if the data is anomalous with respect to any member of the ensemble. We provide a theoretical justification for this approach, proving first that a test on typicality is a valid approach to the goodness-of-fit problem, and then proving that for a correctly constructed ensemble of models, the intersection of typical sets of the models lies in the interior of the typical set of the base distribution. We present our method in the context of an example on synthetic data in which the effects we consider can easily be seen.

DeepReach: A Deep Learning Approach to High-Dimensional Reachability

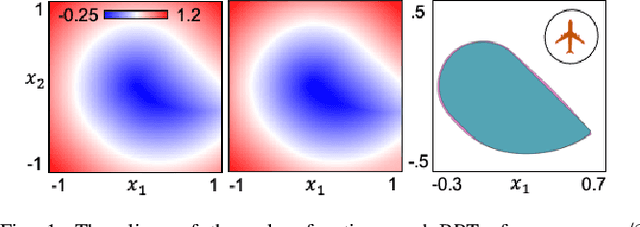
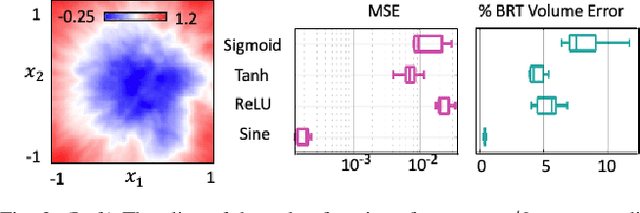
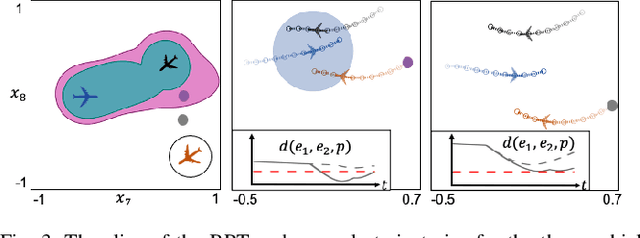
Hamilton-Jacobi (HJ) reachability analysis is an important formal verification method for guaranteeing performance and safety properties of dynamical control systems. Its advantages include compatibility with general nonlinear system dynamics, formal treatment of bounded disturbances, and the ability to deal with state and input constraints. However, it involves solving a PDE, whose computational and memory complexity scales exponentially with respect to the number of state variables, limiting its direct use to small-scale systems. We propose DeepReach, a method that leverages new developments in sinusoidal networks to develop a neural PDE solver for high-dimensional reachability problems. The computational requirements of DeepReach do not scale directly with the state dimension, but rather with the complexity of the underlying reachable tube. DeepReach achieves comparable results to the state-of-the-art reachability methods, does not require any explicit supervision for the PDE solution, can easily handle external disturbances, adversarial inputs, and system constraints, and also provides a safety controller for the system. We demonstrate DeepReach on a 9D multi-vehicle collision problem, and a 10D narrow passage problem, motivated by autonomous driving applications.