What Do Learning Dynamics Reveal About Generalization in LLM Reasoning?

Despite the remarkable capabilities of modern large language models (LLMs), the mechanisms behind their problem-solving abilities remain elusive. In this work, we aim to better understand how the learning dynamics of LLM finetuning shapes downstream generalization. Our analysis focuses on reasoning tasks, whose problem structure allows us to distinguish between memorization (the exact replication of reasoning steps from the training data) and performance (the correctness of the final solution). We find that a model's generalization behavior can be effectively characterized by a training metric we call pre-memorization train accuracy: the accuracy of model samples on training queries before they begin to copy the exact reasoning steps from the training set. On the dataset level, this metric is able to reliably predict test accuracy, achieving $R^2$ of around or exceeding 0.9 across various models (Llama3 8, Gemma2 9B), datasets (GSM8k, MATH), and training configurations. On a per-example level, this metric is also indicative of whether individual model predictions are robust to perturbations in the training query. By connecting a model's learning behavior to its generalization, pre-memorization train accuracy can guide targeted improvements to training strategies. We focus on data curation as an example, and show that prioritizing examples with low pre-memorization accuracy leads to 1.5-2x improvements in data efficiency compared to i.i.d. data scaling, and outperforms other standard data curation techniques.

Unfamiliar Finetuning Examples Control How Language Models Hallucinate

Large language models (LLMs) have a tendency to generate plausible-sounding yet factually incorrect responses, especially when queried on unfamiliar concepts. In this work, we explore the underlying mechanisms that govern how finetuned LLMs hallucinate. Our investigation reveals an interesting pattern: as inputs become more unfamiliar, LLM outputs tend to default towards a ``hedged'' prediction, whose form is determined by how the unfamiliar examples in the finetuning data are supervised. Thus, by strategically modifying these examples' supervision, we can control LLM predictions for unfamiliar inputs (e.g., teach them to say ``I don't know''). Based on these principles, we develop an RL approach that more reliably mitigates hallucinations for long-form generation tasks, by tackling the challenges presented by reward model hallucinations. We validate our findings with a series of controlled experiments in multiple-choice QA on MMLU, as well as long-form biography and book/movie plot generation tasks.

Deep Neural Networks Tend To Extrapolate Predictably

Conventional wisdom suggests that neural network predictions tend to be unpredictable and overconfident when faced with out-of-distribution (OOD) inputs. Our work reassesses this assumption for neural networks with high-dimensional inputs. Rather than extrapolating in arbitrary ways, we observe that neural network predictions often tend towards a constant value as input data becomes increasingly OOD. Moreover, we find that this value often closely approximates the optimal constant solution (OCS), i.e., the prediction that minimizes the average loss over the training data without observing the input. We present results showing this phenomenon across 8 datasets with different distributional shifts (including CIFAR10-C and ImageNet-R, S), different loss functions (cross entropy, MSE, and Gaussian NLL), and different architectures (CNNs and transformers). Furthermore, we present an explanation for this behavior, which we first validate empirically and then study theoretically in a simplified setting involving deep homogeneous networks with ReLU activations. Finally, we show how one can leverage our insights in practice to enable risk-sensitive decision-making in the presence of OOD inputs.

Multi-Task Imitation Learning for Linear Dynamical Systems

We study representation learning for efficient imitation learning over linear systems. In particular, we consider a setting where learning is split into two phases: (a) a pre-training step where a shared $k$-dimensional representation is learned from $H$ source policies, and (b) a target policy fine-tuning step where the learned representation is used to parameterize the policy class. We find that the imitation gap over trajectories generated by the learned target policy is bounded by $\tilde{O}\left( \frac{k n_x}{HN_{\mathrm{shared}}} + \frac{k n_u}{N_{\mathrm{target}}}\right)$, where $n_x > k$ is the state dimension, $n_u$ is the input dimension, $N_{\mathrm{shared}}$ denotes the total amount of data collected for each policy during representation learning, and $N_{\mathrm{target}}$ is the amount of target task data. This result formalizes the intuition that aggregating data across related tasks to learn a representation can significantly improve the sample efficiency of learning a target task. The trends suggested by this bound are corroborated in simulation.

Lyapunov Density Models: Constraining Distribution Shift in Learning-Based Control

Learned models and policies can generalize effectively when evaluated within the distribution of the training data, but can produce unpredictable and erroneous outputs on out-of-distribution inputs. In order to avoid distribution shift when deploying learning-based control algorithms, we seek a mechanism to constrain the agent to states and actions that resemble those that it was trained on. In control theory, Lyapunov stability and control-invariant sets allow us to make guarantees about controllers that stabilize the system around specific states, while in machine learning, density models allow us to estimate the training data distribution. Can we combine these two concepts, producing learning-based control algorithms that constrain the system to in-distribution states using only in-distribution actions? In this work, we propose to do this by combining concepts from Lyapunov stability and density estimation, introducing Lyapunov density models: a generalization of control Lyapunov functions and density models that provides guarantees on an agent's ability to stay in-distribution over its entire trajectory.

Multi-Robot Deep Reinforcement Learning for Mobile Navigation

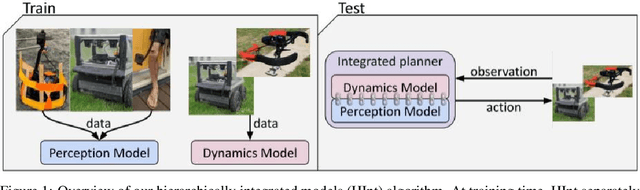
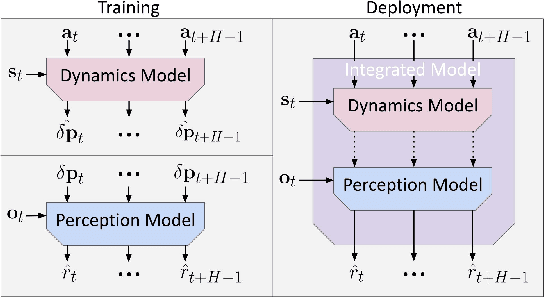
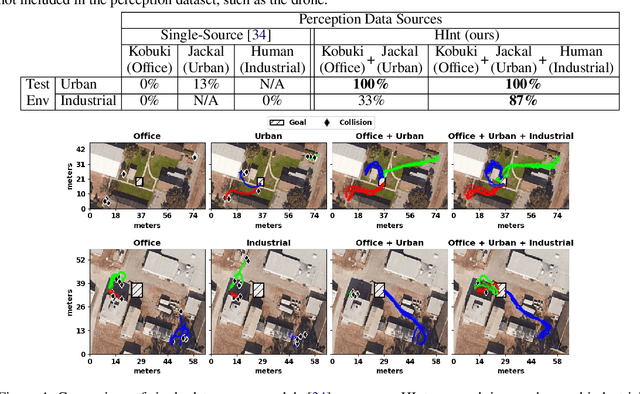
Deep reinforcement learning algorithms require large and diverse datasets in order to learn successful policies for perception-based mobile navigation. However, gathering such datasets with a single robot can be prohibitively expensive. Collecting data with multiple different robotic platforms with possibly different dynamics is a more scalable approach to large-scale data collection. But how can deep reinforcement learning algorithms leverage such heterogeneous datasets? In this work, we propose a deep reinforcement learning algorithm with hierarchically integrated models (HInt). At training time, HInt learns separate perception and dynamics models, and at test time, HInt integrates the two models in a hierarchical manner and plans actions with the integrated model. This method of planning with hierarchically integrated models allows the algorithm to train on datasets gathered by a variety of different platforms, while respecting the physical capabilities of the deployment robot at test time. Our mobile navigation experiments show that HInt outperforms conventional hierarchical policies and single-source approaches.

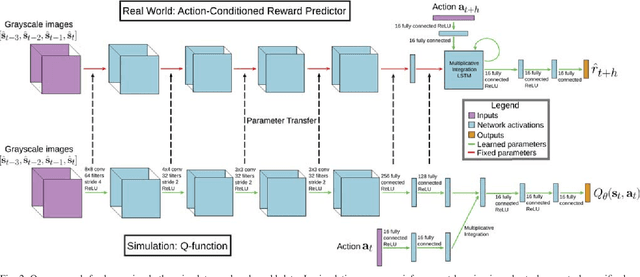
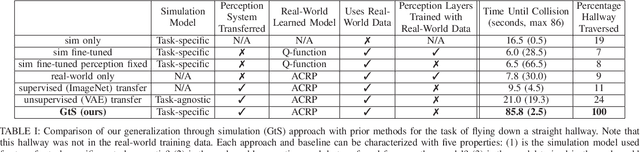
Generalization through Simulation: Integrating Simulated and Real Data into Deep Reinforcement Learning for Vision-Based Autonomous Flight

Deep reinforcement learning provides a promising approach for vision-based control of real-world robots. However, the generalization of such models depends critically on the quantity and variety of data available for training. This data can be difficult to obtain for some types of robotic systems, such as fragile, small-scale quadrotors. Simulated rendering and physics can provide for much larger datasets, but such data is inherently of lower quality: many of the phenomena that make the real-world autonomous flight problem challenging, such as complex physics and air currents, are modeled poorly or not at all, and the systematic differences between simulation and the real world are typically impossible to eliminate. In this work, we investigate how data from both simulation and the real world can be combined in a hybrid deep reinforcement learning algorithm. Our method uses real-world data to learn about the dynamics of the system, and simulated data to learn a generalizable perception system that can enable the robot to avoid collisions using only a monocular camera. We demonstrate our approach on a real-world nano aerial vehicle collision avoidance task, showing that with only an hour of real-world data, the quadrotor can avoid collisions in new environments with various lighting conditions and geometry. Code, instructions for building the aerial vehicles, and videos of the experiments can be found at github.com/gkahn13/GtS