Kristofer Bouchard
Towards Reverse-Engineering the Brain: Brain-Derived Neuromorphic Computing Approach with Photonic, Electronic, and Ionic Dynamicity in 3D integrated circuits
Mar 28, 2024



Abstract:The human brain has immense learning capabilities at extreme energy efficiencies and scale that no artificial system has been able to match. For decades, reverse engineering the brain has been one of the top priorities of science and technology research. Despite numerous efforts, conventional electronics-based methods have failed to match the scalability, energy efficiency, and self-supervised learning capabilities of the human brain. On the other hand, very recent progress in the development of new generations of photonic and electronic memristive materials, device technologies, and 3D electronic-photonic integrated circuits (3D EPIC ) promise to realize new brain-derived neuromorphic systems with comparable connectivity, density, energy-efficiency, and scalability. When combined with bio-realistic learning algorithms and architectures, it may be possible to realize an 'artificial brain' prototype with general self-learning capabilities. This paper argues the possibility of reverse-engineering the brain through architecting a prototype of a brain-derived neuromorphic computing system consisting of artificial electronic, ionic, photonic materials, devices, and circuits with dynamicity resembling the bio-plausible molecular, neuro/synaptic, neuro-circuit, and multi-structural hierarchical macro-circuits of the brain based on well-tested computational models. We further argue the importance of bio-plausible local learning algorithms applicable to the neuromorphic computing system that capture the flexible and adaptive unsupervised and self-supervised learning mechanisms central to human intelligence. Most importantly, we emphasize that the unique capabilities in brain-derived neuromorphic computing prototype systems will enable us to understand links between specific neuronal and network-level properties with system-level functioning and behavior.
Compressed Predictive Information Coding
Mar 03, 2022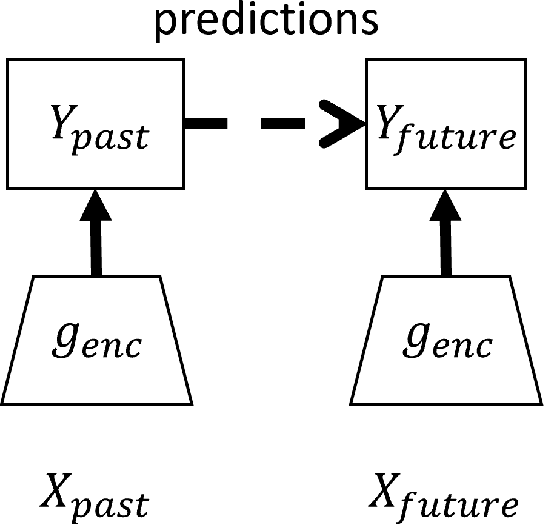
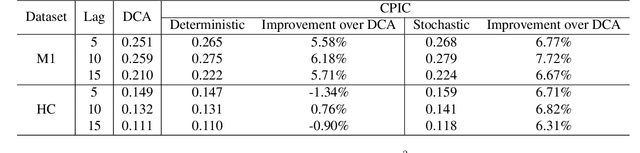
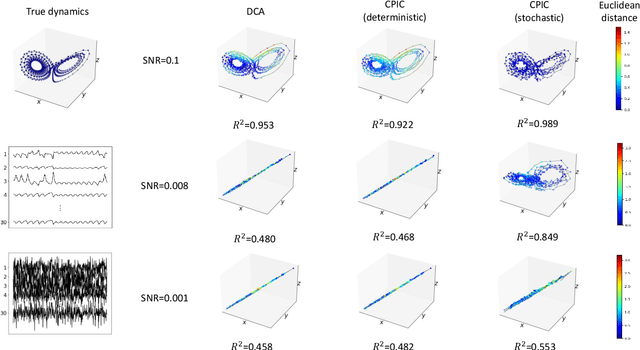
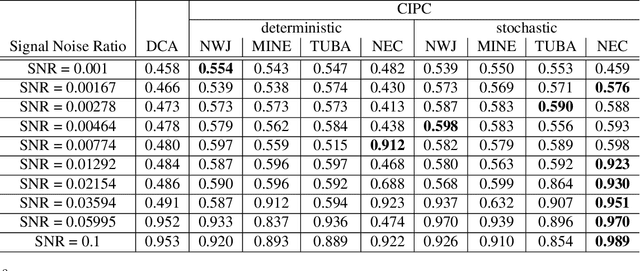
Abstract:Unsupervised learning plays an important role in many fields, such as artificial intelligence, machine learning, and neuroscience. Compared to static data, methods for extracting low-dimensional structure for dynamic data are lagging. We developed a novel information-theoretic framework, Compressed Predictive Information Coding (CPIC), to extract useful representations from dynamic data. CPIC selectively projects the past (input) into a linear subspace that is predictive about the compressed data projected from the future (output). The key insight of our framework is to learn representations by minimizing the compression complexity and maximizing the predictive information in latent space. We derive variational bounds of the CPIC loss which induces the latent space to capture information that is maximally predictive. Our variational bounds are tractable by leveraging bounds of mutual information. We find that introducing stochasticity in the encoder robustly contributes to better representation. Furthermore, variational approaches perform better in mutual information estimation compared with estimates under a Gaussian assumption. We demonstrate that CPIC is able to recover the latent space of noisy dynamical systems with low signal-to-noise ratios, and extracts features predictive of exogenous variables in neuroscience data.
Learning from learning machines: a new generation of AI technology to meet the needs of science
Nov 27, 2021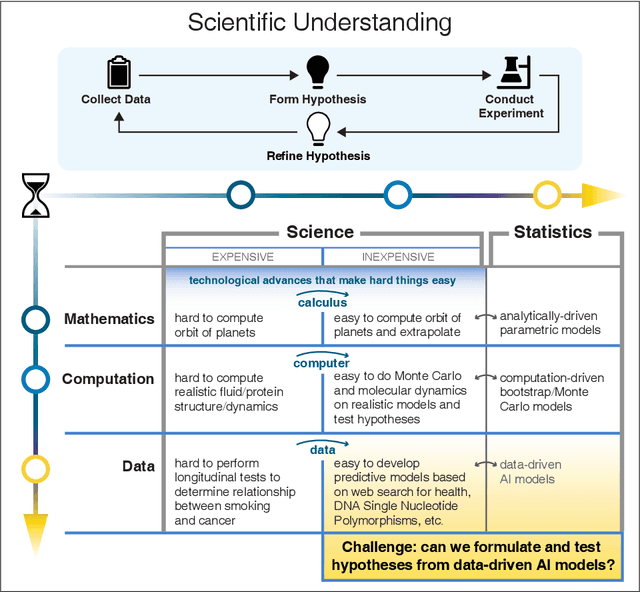

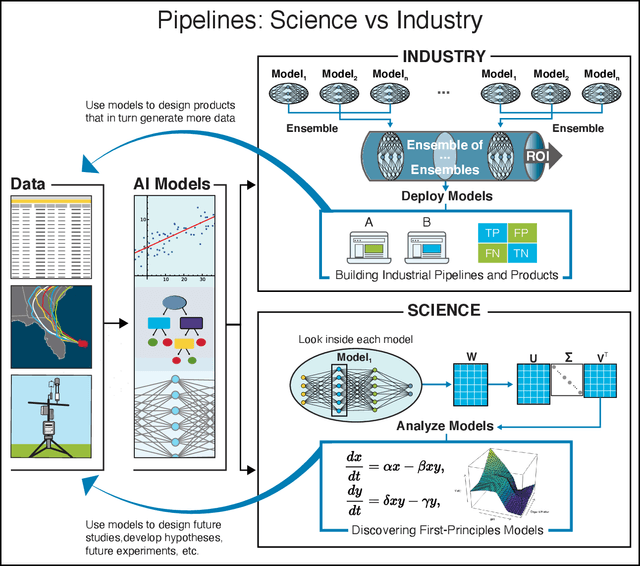
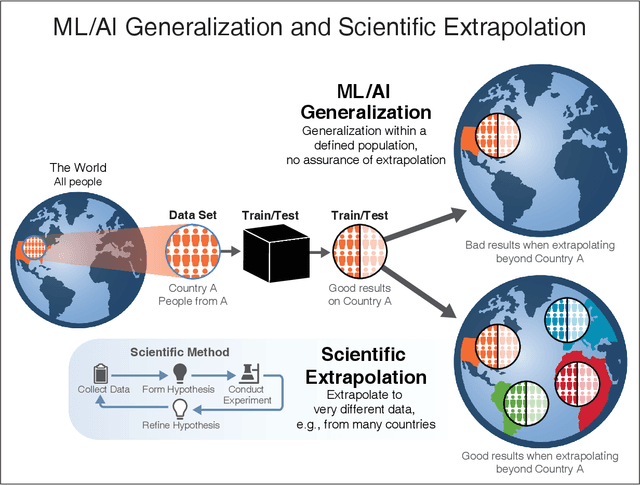
Abstract:We outline emerging opportunities and challenges to enhance the utility of AI for scientific discovery. The distinct goals of AI for industry versus the goals of AI for science create tension between identifying patterns in data versus discovering patterns in the world from data. If we address the fundamental challenges associated with "bridging the gap" between domain-driven scientific models and data-driven AI learning machines, then we expect that these AI models can transform hypothesis generation, scientific discovery, and the scientific process itself.
Bayesian Inference in High-Dimensional Time-Serieswith the Orthogonal Stochastic Linear Mixing Model
Jun 25, 2021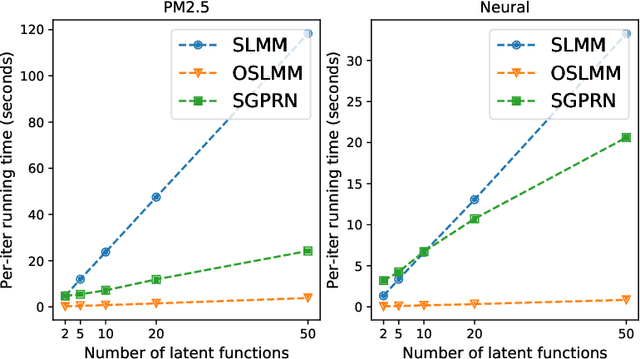
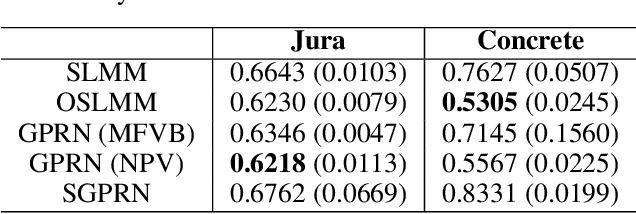
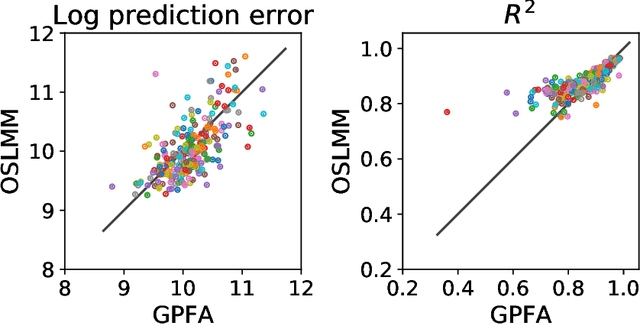
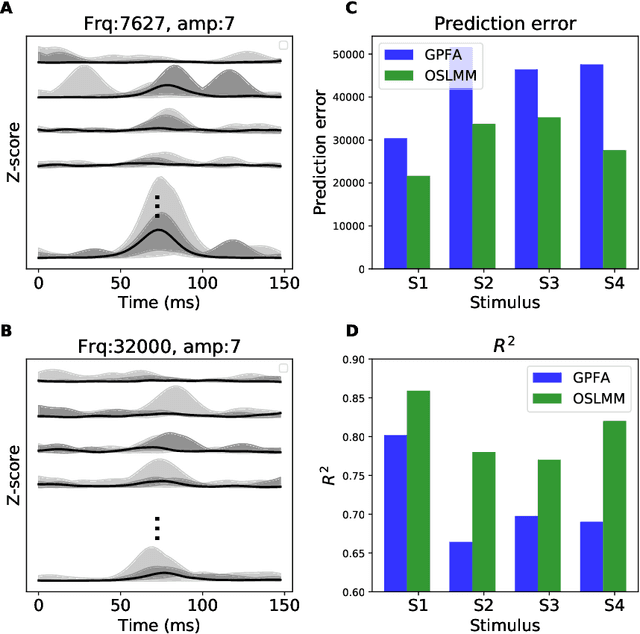
Abstract:Many modern time-series datasets contain large numbers of output response variables sampled for prolonged periods of time. For example, in neuroscience, the activities of 100s-1000's of neurons are recorded during behaviors and in response to sensory stimuli. Multi-output Gaussian process models leverage the nonparametric nature of Gaussian processes to capture structure across multiple outputs. However, this class of models typically assumes that the correlations between the output response variables are invariant in the input space. Stochastic linear mixing models (SLMM) assume the mixture coefficients depend on input, making them more flexible and effective to capture complex output dependence. However, currently, the inference for SLMMs is intractable for large datasets, making them inapplicable to several modern time-series problems. In this paper, we propose a new regression framework, the orthogonal stochastic linear mixing model (OSLMM) that introduces an orthogonal constraint amongst the mixing coefficients. This constraint reduces the computational burden of inference while retaining the capability to handle complex output dependence. We provide Markov chain Monte Carlo inference procedures for both SLMM and OSLMM and demonstrate superior model scalability and reduced prediction error of OSLMM compared with state-of-the-art methods on several real-world applications. In neurophysiology recordings, we use the inferred latent functions for compact visualization of population responses to auditory stimuli, and demonstrate superior results compared to a competing method (GPFA). Together, these results demonstrate that OSLMM will be useful for the analysis of diverse, large-scale time-series datasets.
Collaborative Nonstationary Multivariate Gaussian Process Model
Jun 01, 2021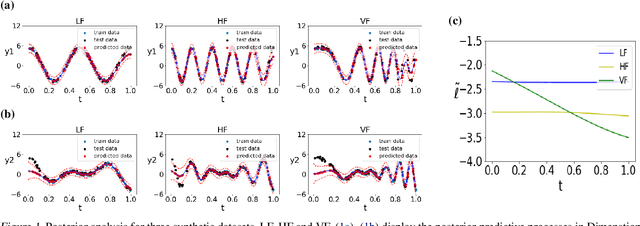
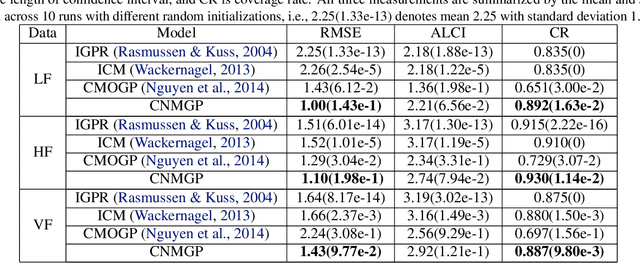
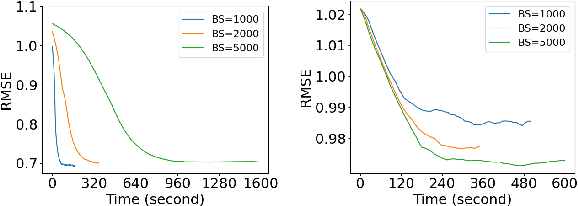

Abstract:Currently, multi-output Gaussian process regression models either do not model nonstationarity or are associated with severe computational burdens and storage demands. Nonstationary multi-variate Gaussian process models (NMGP) use a nonstationary covariance function with an input-dependent linear model of coregionalisation to jointly model input-dependent correlation, scale, and smoothness of outputs. Variational sparse approximation relies on inducing points to enable scalable computations. Here, we take the best of both worlds: considering an inducing variable framework on the underlying latent functions in NMGP, we propose a novel model called the collaborative nonstationary Gaussian process model(CNMGP). For CNMGP, we derive computationally tractable variational bounds amenable to doubly stochastic variational inference. Together, this allows us to model data in which outputs do not share a common input set, with a computational complexity that is independent of the size of the inputs and outputs. We illustrate the performance of our method on synthetic data and three real datasets and show that our model generally pro-vides better predictive performance than the state-of-the-art, and also provides estimates of time-varying correlations that differ across outputs.
Run Procrustes, Run! On the convergence of accelerated Procrustes Flow
Sep 12, 2018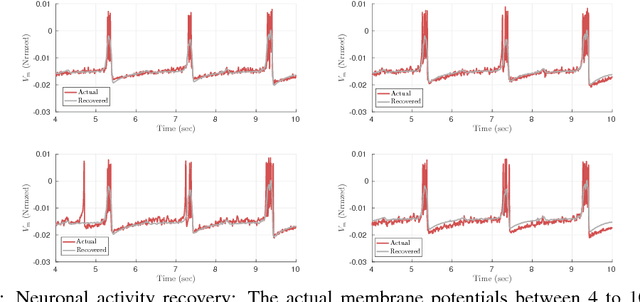
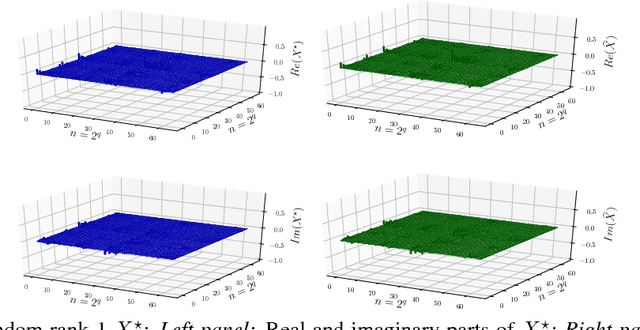
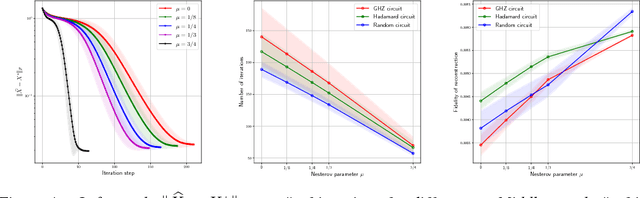
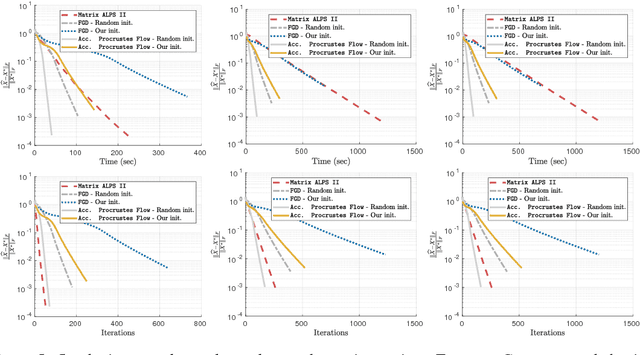
Abstract:In this work, we present theoretical results on the convergence of non-convex accelerated gradient descent in matrix factorization models. The technique is applied to matrix sensing problems with squared loss, for the estimation of a rank $r$ optimal solution $X^\star \in \mathbb{R}^{n \times n}$. We show that the acceleration leads to linear convergence rate, even under non-convex settings where the variable $X$ is represented as $U U^\top$ for $U \in \mathbb{R}^{n \times r}$. Our result has the same dependence on the condition number of the objective --and the optimal solution-- as that of the recent results on non-accelerated algorithms. However, acceleration is observed in practice, both in synthetic examples and in two real applications: neuronal multi-unit activities recovery from single electrode recordings, and quantum state tomography on quantum computing simulators.
Optimizing the Union of Intersections LASSO ($UoI_{LASSO}$) and Vector Autoregressive ($UoI_{VAR}$) Algorithms for Improved Statistical Estimation at Scale
Aug 21, 2018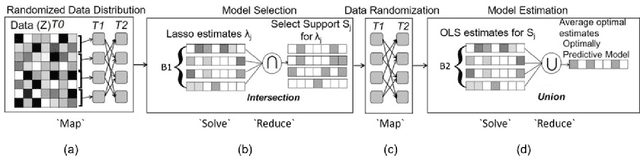
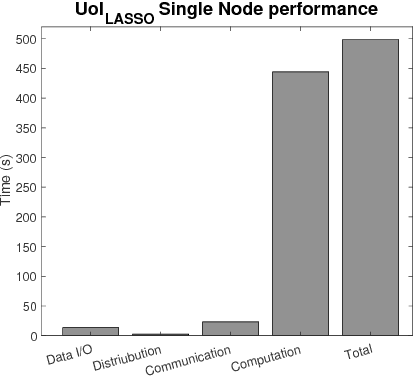
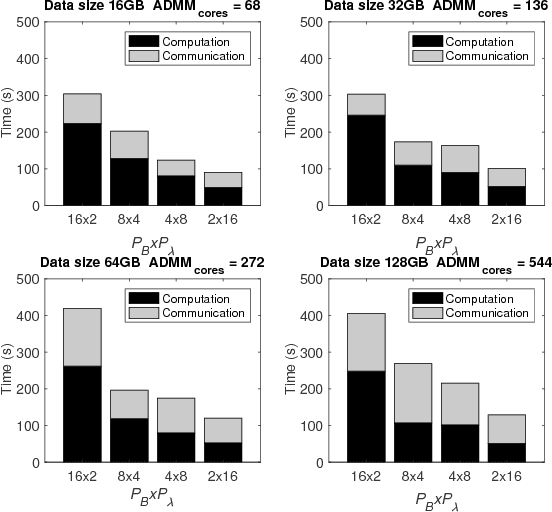
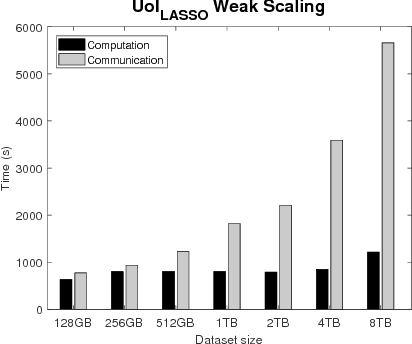
Abstract:The analysis of scientific data of increasing size and complexity requires statistical machine learning methods that are both interpretable and predictive. Union of Intersections (UoI), a recently developed framework, is a two-step approach that separates model selection and model estimation. A linear regression algorithm based on UoI, $UoI_{LASSO}$, simultaneously achieves low false positives and low false negative feature selection as well as low bias and low variance estimates. Together, these qualities make the results both predictive and interpretable. In this paper, we optimize the $UoI_{LASSO}$ algorithm for single-node execution on NERSC's Cori Knights Landing, a Xeon Phi based supercomputer. We then scale $UoI_{LASSO}$ to execute on cores ranging from 68-278,528 cores on a range of dataset sizes demonstrating the weak and strong scaling of the implementation. We also implement a variant of $UoI_{LASSO}$, $UoI_{VAR}$ for vector autoregressive models, to analyze high dimensional time-series data. We perform single node optimization and multi-node scaling experiments for $UoI_{VAR}$ to demonstrate the effectiveness of the algorithm for weak and strong scaling. Our implementations enable to use estimate the largest VAR model (1000 nodes) we are aware of, and apply it to large neurophysiology data 192 nodes).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge