A Posterior Sampling Framework for Interactive Decision Making

We study sample efficient reinforcement learning (RL) under the general framework of interactive decision making, which includes Markov decision process (MDP), partially observable Markov decision process (POMDP), and predictive state representation (PSR) as special cases. Toward finding the minimum assumption that empowers sample efficient learning, we propose a novel complexity measure, generalized eluder coefficient (GEC), which characterizes the fundamental tradeoff between exploration and exploitation in online interactive decision making. In specific, GEC captures the hardness of exploration by comparing the error of predicting the performance of the updated policy with the in-sample training error evaluated on the historical data. We show that RL problems with low GEC form a remarkably rich class, which subsumes low Bellman eluder dimension problems, bilinear class, low witness rank problems, PO-bilinear class, and generalized regular PSR, where generalized regular PSR, a new tractable PSR class identified by us, includes nearly all known tractable POMDPs. Furthermore, in terms of algorithm design, we propose a generic posterior sampling algorithm, which can be implemented in both model-free and model-based fashion, under both fully observable and partially observable settings. The proposed algorithm modifies the standard posterior sampling algorithm in two aspects: (i) we use an optimistic prior distribution that biases towards hypotheses with higher values and (ii) a loglikelihood function is set to be the empirical loss evaluated on the historical data, where the choice of loss function supports both model-free and model-based learning. We prove that the proposed algorithm is sample efficient by establishing a sublinear regret upper bound in terms of GEC. In summary, we provide a new and unified understanding of both fully observable and partially observable RL.

A Reinforcement Learning Approach in Multi-Phase Second-Price Auction Design

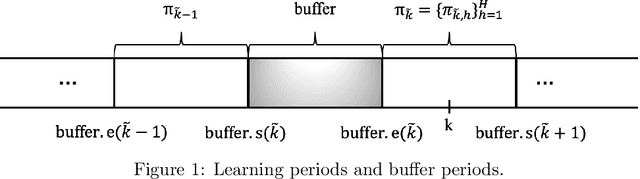
We study reserve price optimization in multi-phase second price auctions, where seller's prior actions affect the bidders' later valuations through a Markov Decision Process (MDP). Compared to the bandit setting in existing works, the setting in ours involves three challenges. First, from the seller's perspective, we need to efficiently explore the environment in the presence of potentially nontruthful bidders who aim to manipulates seller's policy. Second, we want to minimize the seller's revenue regret when the market noise distribution is unknown. Third, the seller's per-step revenue is unknown, nonlinear, and cannot even be directly observed from the environment. We propose a mechanism addressing all three challenges. To address the first challenge, we use a combination of a new technique named "buffer periods" and inspirations from Reinforcement Learning (RL) with low switching cost to limit bidders' surplus from untruthful bidding, thereby incentivizing approximately truthful bidding. The second one is tackled by a novel algorithm that removes the need for pure exploration when the market noise distribution is unknown. The third challenge is resolved by an extension of LSVI-UCB, where we use the auction's underlying structure to control the uncertainty of the revenue function. The three techniques culminate in the $\underline{\rm C}$ontextual-$\underline{\rm L}$SVI-$\underline{\rm U}$CB-$\underline{\rm B}$uffer (CLUB) algorithm which achieves $\tilde{ \mathcal{O}}(H^{5/2}\sqrt{K})$ revenue regret when the market noise is known and $\tilde{ \mathcal{O}}(H^{3}\sqrt{K})$ revenue regret when the noise is unknown with no assumptions on bidders' truthfulness.

Enforcing Hard Constraints with Soft Barriers: Safe Reinforcement Learning in Unknown Stochastic Environments

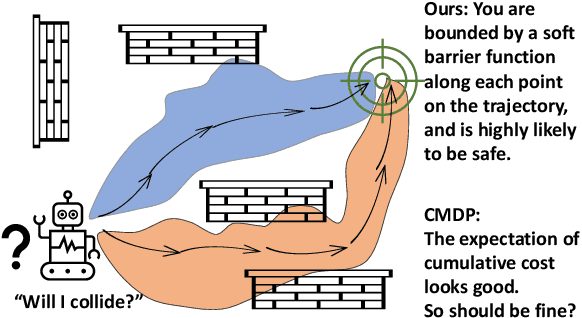
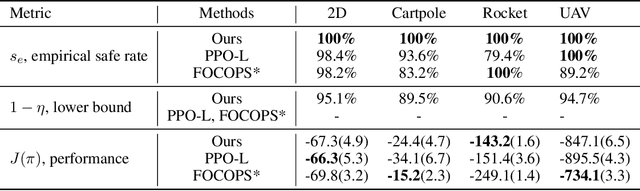
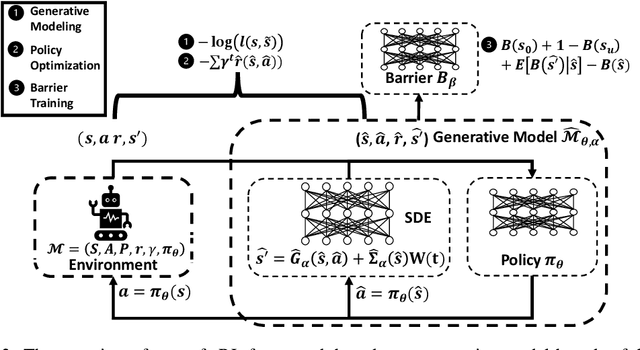
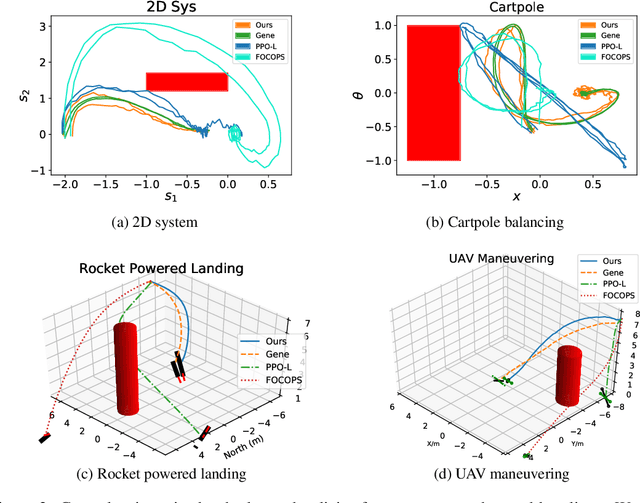
It is quite challenging to ensure the safety of reinforcement learning (RL) agents in an unknown and stochastic environment under hard constraints that require the system state not to reach certain specified unsafe regions. Many popular safe RL methods such as those based on the Constrained Markov Decision Process (CMDP) paradigm formulate safety violations in a cost function and try to constrain the expectation of cumulative cost under a threshold. However, it is often difficult to effectively capture and enforce hard reachability-based safety constraints indirectly with such constraints on safety violation costs. In this work, we leverage the notion of barrier function to explicitly encode the hard safety constraints, and given that the environment is unknown, relax them to our design of \emph{generative-model-based soft barrier functions}. Based on such soft barriers, we propose a safe RL approach that can jointly learn the environment and optimize the control policy, while effectively avoiding unsafe regions with safety probability optimization. Experiments on a set of examples demonstrate that our approach can effectively enforce hard safety constraints and significantly outperform CMDP-based baseline methods in system safe rate measured via simulations.

Relational Reasoning via Set Transformers: Provable Efficiency and Applications to MARL

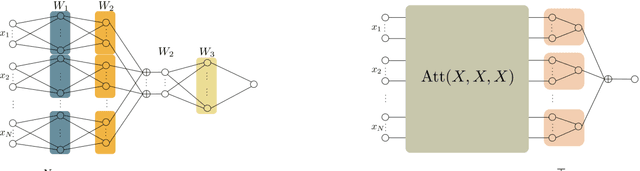
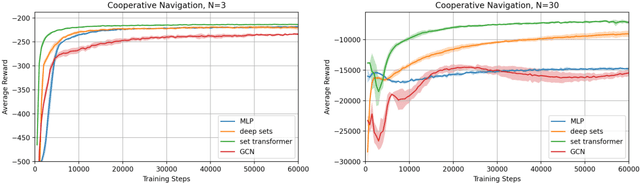
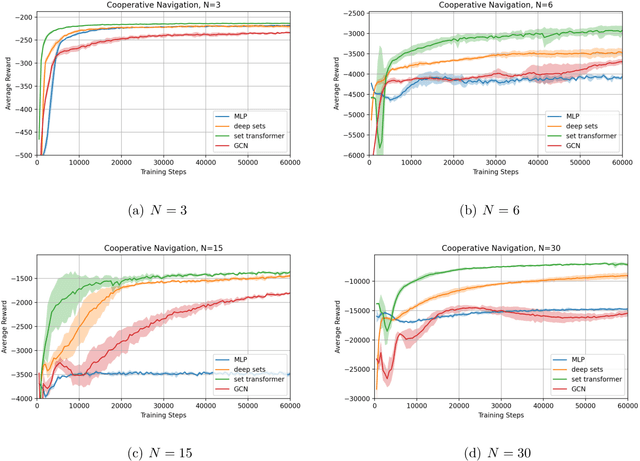
The cooperative Multi-A gent R einforcement Learning (MARL) with permutation invariant agents framework has achieved tremendous empirical successes in real-world applications. Unfortunately, the theoretical understanding of this MARL problem is lacking due to the curse of many agents and the limited exploration of the relational reasoning in existing works. In this paper, we verify that the transformer implements complex relational reasoning, and we propose and analyze model-free and model-based offline MARL algorithms with the transformer approximators. We prove that the suboptimality gaps of the model-free and model-based algorithms are independent of and logarithmic in the number of agents respectively, which mitigates the curse of many agents. These results are consequences of a novel generalization error bound of the transformer and a novel analysis of the Maximum Likelihood Estimate (MLE) of the system dynamics with the transformer. Our model-based algorithm is the first provably efficient MARL algorithm that explicitly exploits the permutation invariance of the agents.

Offline Reinforcement Learning with Instrumental Variables in Confounded Markov Decision Processes

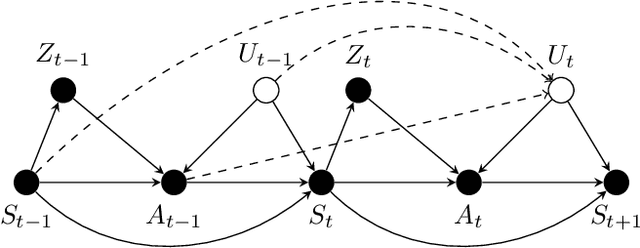
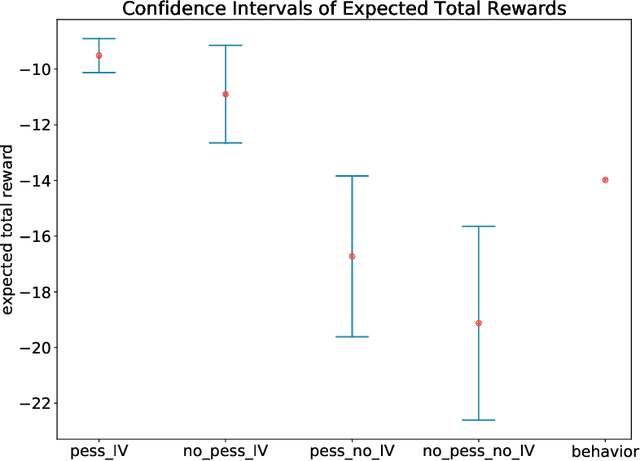
We study the offline reinforcement learning (RL) in the face of unmeasured confounders. Due to the lack of online interaction with the environment, offline RL is facing the following two significant challenges: (i) the agent may be confounded by the unobserved state variables; (ii) the offline data collected a prior does not provide sufficient coverage for the environment. To tackle the above challenges, we study the policy learning in the confounded MDPs with the aid of instrumental variables. Specifically, we first establish value function (VF)-based and marginalized importance sampling (MIS)-based identification results for the expected total reward in the confounded MDPs. Then by leveraging pessimism and our identification results, we propose various policy learning methods with the finite-sample suboptimality guarantee of finding the optimal in-class policy under minimal data coverage and modeling assumptions. Lastly, our extensive theoretical investigations and one numerical study motivated by the kidney transplantation demonstrate the promising performance of the proposed methods.

Strategic Decision-Making in the Presence of Information Asymmetry: Provably Efficient RL with Algorithmic Instruments

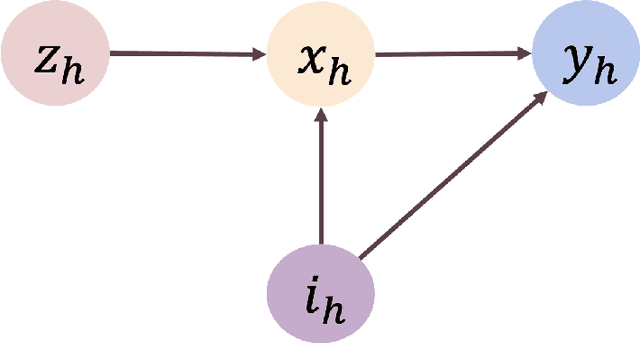
We study offline reinforcement learning under a novel model called strategic MDP, which characterizes the strategic interactions between a principal and a sequence of myopic agents with private types. Due to the bilevel structure and private types, strategic MDP involves information asymmetry between the principal and the agents. We focus on the offline RL problem, where the goal is to learn the optimal policy of the principal concerning a target population of agents based on a pre-collected dataset that consists of historical interactions. The unobserved private types confound such a dataset as they affect both the rewards and observations received by the principal. We propose a novel algorithm, Pessimistic policy Learning with Algorithmic iNstruments (PLAN), which leverages the ideas of instrumental variable regression and the pessimism principle to learn a near-optimal principal's policy in the context of general function approximation. Our algorithm is based on the critical observation that the principal's actions serve as valid instrumental variables. In particular, under a partial coverage assumption on the offline dataset, we prove that PLAN outputs a $1 / \sqrt{K}$-optimal policy with $K$ being the number of collected trajectories. We further apply our framework to some special cases of strategic MDP, including strategic regression, strategic bandit, and noncompliance in recommendation systems.

Contrastive UCB: Provably Efficient Contrastive Self-Supervised Learning in Online Reinforcement Learning

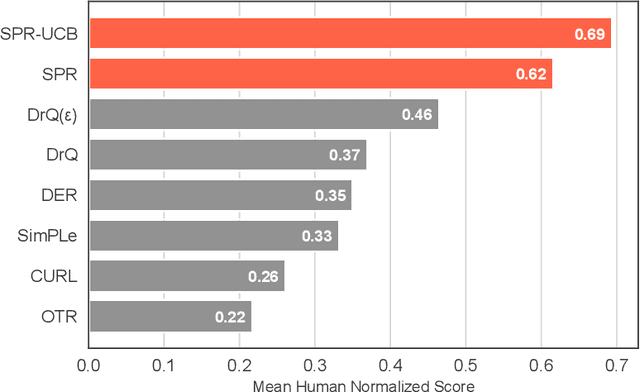
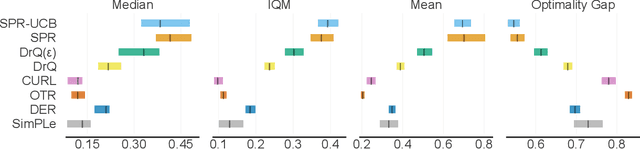
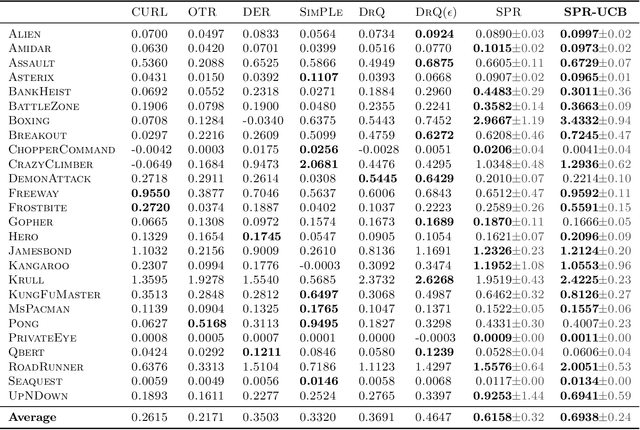
In view of its power in extracting feature representation, contrastive self-supervised learning has been successfully integrated into the practice of (deep) reinforcement learning (RL), leading to efficient policy learning in various applications. Despite its tremendous empirical successes, the understanding of contrastive learning for RL remains elusive. To narrow such a gap, we study how RL can be empowered by contrastive learning in a class of Markov decision processes (MDPs) and Markov games (MGs) with low-rank transitions. For both models, we propose to extract the correct feature representations of the low-rank model by minimizing a contrastive loss. Moreover, under the online setting, we propose novel upper confidence bound (UCB)-type algorithms that incorporate such a contrastive loss with online RL algorithms for MDPs or MGs. We further theoretically prove that our algorithm recovers the true representations and simultaneously achieves sample efficiency in learning the optimal policy and Nash equilibrium in MDPs and MGs. We also provide empirical studies to demonstrate the efficacy of the UCB-based contrastive learning method for RL. To the best of our knowledge, we provide the first provably efficient online RL algorithm that incorporates contrastive learning for representation learning. Our codes are available at https://github.com/Baichenjia/Contrastive-UCB.

Provably Efficient Fictitious Play Policy Optimization for Zero-Sum Markov Games with Structured Transitions

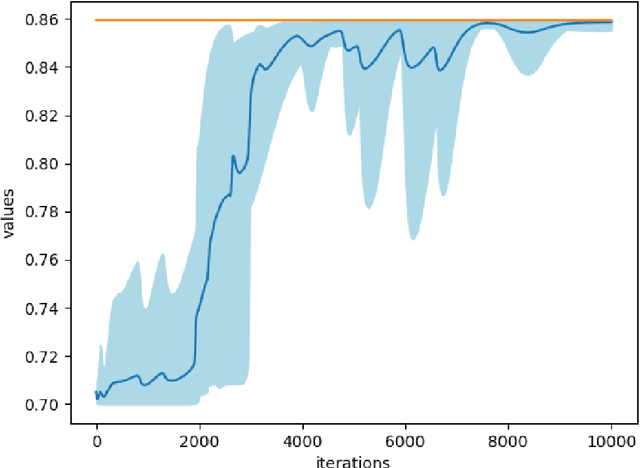
While single-agent policy optimization in a fixed environment has attracted a lot of research attention recently in the reinforcement learning community, much less is known theoretically when there are multiple agents playing in a potentially competitive environment. We take steps forward by proposing and analyzing new fictitious play policy optimization algorithms for zero-sum Markov games with structured but unknown transitions. We consider two classes of transition structures: factored independent transition and single-controller transition. For both scenarios, we prove tight $\widetilde{\mathcal{O}}(\sqrt{K})$ regret bounds after $K$ episodes in a two-agent competitive game scenario. The regret of each agent is measured against a potentially adversarial opponent who can choose a single best policy in hindsight after observing the full policy sequence. Our algorithms feature a combination of Upper Confidence Bound (UCB)-type optimism and fictitious play under the scope of simultaneous policy optimization in a non-stationary environment. When both players adopt the proposed algorithms, their overall optimality gap is $\widetilde{\mathcal{O}}(\sqrt{K})$.

Decentralized Optimistic Hyperpolicy Mirror Descent: Provably No-Regret Learning in Markov Games

We study decentralized policy learning in Markov games where we control a single agent to play with nonstationary and possibly adversarial opponents. Our goal is to develop a no-regret online learning algorithm that (i) takes actions based on the local information observed by the agent and (ii) is able to find the best policy in hindsight. For such a problem, the nonstationary state transitions due to the varying opponent pose a significant challenge. In light of a recent hardness result \citep{liu2022learning}, we focus on the setting where the opponent's previous policies are revealed to the agent for decision making. With such an information structure, we propose a new algorithm, \underline{D}ecentralized \underline{O}ptimistic hype\underline{R}policy m\underline{I}rror de\underline{S}cent (DORIS), which achieves $\sqrt{K}$-regret in the context of general function approximation, where $K$ is the number of episodes. Moreover, when all the agents adopt DORIS, we prove that their mixture policy constitutes an approximate coarse correlated equilibrium. In particular, DORIS maintains a \textit{hyperpolicy} which is a distribution over the policy space. The hyperpolicy is updated via mirror descent, where the update direction is obtained by an optimistic variant of least-squares policy evaluation. Furthermore, to illustrate the power of our method, we apply DORIS to constrained and vector-valued MDPs, which can be formulated as zero-sum Markov games with a fictitious opponent.

Pessimism in the Face of Confounders: Provably Efficient Offline Reinforcement Learning in Partially Observable Markov Decision Processes

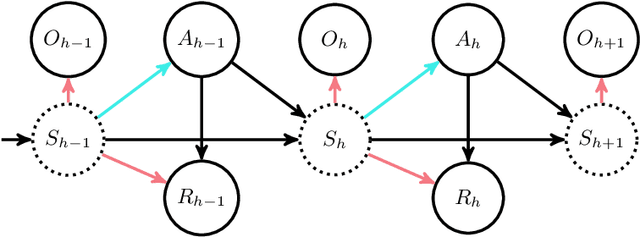
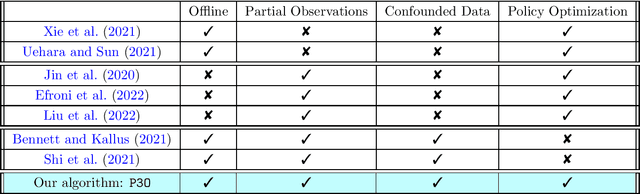
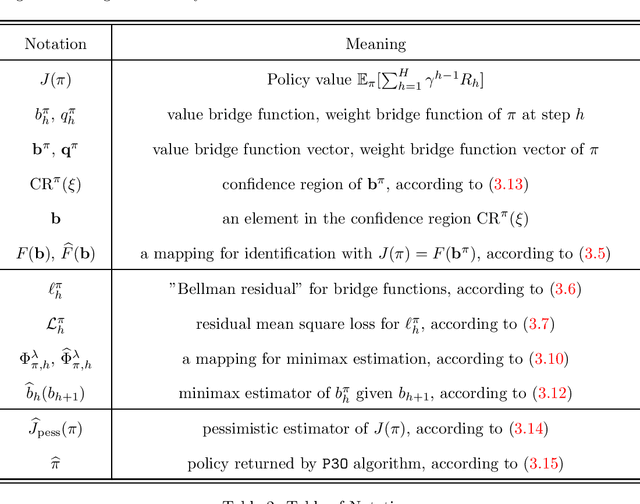
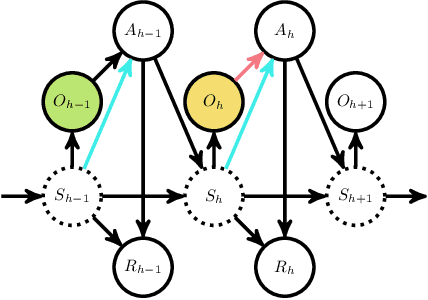
We study offline reinforcement learning (RL) in partially observable Markov decision processes. In particular, we aim to learn an optimal policy from a dataset collected by a behavior policy which possibly depends on the latent state. Such a dataset is confounded in the sense that the latent state simultaneously affects the action and the observation, which is prohibitive for existing offline RL algorithms. To this end, we propose the \underline{P}roxy variable \underline{P}essimistic \underline{P}olicy \underline{O}ptimization (\texttt{P3O}) algorithm, which addresses the confounding bias and the distributional shift between the optimal and behavior policies in the context of general function approximation. At the core of \texttt{P3O} is a coupled sequence of pessimistic confidence regions constructed via proximal causal inference, which is formulated as minimax estimation. Under a partial coverage assumption on the confounded dataset, we prove that \texttt{P3O} achieves a $n^{-1/2}$-suboptimality, where $n$ is the number of trajectories in the dataset. To our best knowledge, \texttt{P3O} is the first provably efficient offline RL algorithm for POMDPs with a confounded dataset.