Pessimism in the Face of Confounders: Provably Efficient Offline Reinforcement Learning in Partially Observable Markov Decision Processes
Paper and Code
May 26, 2022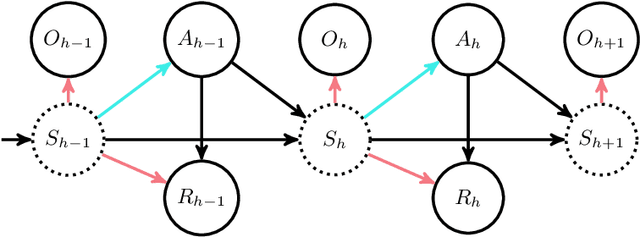
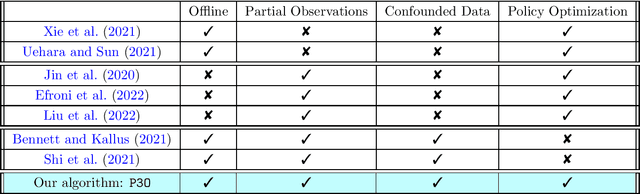
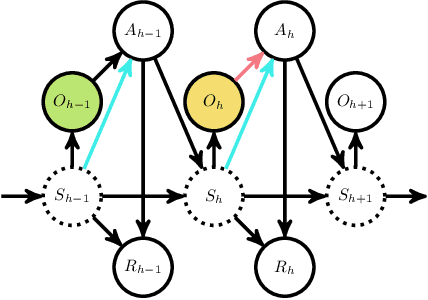
We study offline reinforcement learning (RL) in partially observable Markov decision processes. In particular, we aim to learn an optimal policy from a dataset collected by a behavior policy which possibly depends on the latent state. Such a dataset is confounded in the sense that the latent state simultaneously affects the action and the observation, which is prohibitive for existing offline RL algorithms. To this end, we propose the \underline{P}roxy variable \underline{P}essimistic \underline{P}olicy \underline{O}ptimization (\texttt{P3O}) algorithm, which addresses the confounding bias and the distributional shift between the optimal and behavior policies in the context of general function approximation. At the core of \texttt{P3O} is a coupled sequence of pessimistic confidence regions constructed via proximal causal inference, which is formulated as minimax estimation. Under a partial coverage assumption on the confounded dataset, we prove that \texttt{P3O} achieves a $n^{-1/2}$-suboptimality, where $n$ is the number of trajectories in the dataset. To our best knowledge, \texttt{P3O} is the first provably efficient offline RL algorithm for POMDPs with a confounded dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge