Covariate Assisted Entity Ranking with Sparse Intrinsic Scores

This paper addresses the item ranking problem with associate covariates, focusing on scenarios where the preference scores can not be fully explained by covariates, and the remaining intrinsic scores, are sparse. Specifically, we extend the pioneering Bradley-Terry-Luce (BTL) model by incorporating covariate information and considering sparse individual intrinsic scores. Our work introduces novel model identification conditions and examines the regularized penalized Maximum Likelihood Estimator (MLE) statistical rates. We then construct a debiased estimator for the penalized MLE and analyze its distributional properties. Additionally, we apply our method to the goodness-of-fit test for models with no latent intrinsic scores, namely, the covariates fully explaining the preference scores of individual items. We also offer confidence intervals for ranks. Our numerical studies lend further support to our theoretical findings, demonstrating validation for our proposed method

Uncertainty in Language Models: Assessment through Rank-Calibration

Language Models (LMs) have shown promising performance in natural language generation. However, as LMs often generate incorrect or hallucinated responses, it is crucial to correctly quantify their uncertainty in responding to given inputs. In addition to verbalized confidence elicited via prompting, many uncertainty measures ($e.g.$, semantic entropy and affinity-graph-based measures) have been proposed. However, these measures can differ greatly, and it is unclear how to compare them, partly because they take values over different ranges ($e.g.$, $[0,\infty)$ or $[0,1]$). In this work, we address this issue by developing a novel and practical framework, termed $Rank$-$Calibration$, to assess uncertainty and confidence measures for LMs. Our key tenet is that higher uncertainty (or lower confidence) should imply lower generation quality, on average. Rank-calibration quantifies deviations from this ideal relationship in a principled manner, without requiring ad hoc binary thresholding of the correctness score ($e.g.$, ROUGE or METEOR). The broad applicability and the granular interpretability of our methods are demonstrated empirically.

SymmPI: Predictive Inference for Data with Group Symmetries

Quantifying the uncertainty of predictions is a core problem in modern statistics. Methods for predictive inference have been developed under a variety of assumptions, often -- for instance, in standard conformal prediction -- relying on the invariance of the distribution of the data under special groups of transformations such as permutation groups. Moreover, many existing methods for predictive inference aim to predict unobserved outcomes in sequences of feature-outcome observations. Meanwhile, there is interest in predictive inference under more general observation models (e.g., for partially observed features) and for data satisfying more general distributional symmetries (e.g., rotationally invariant or coordinate-independent observations in physics). Here we propose SymmPI, a methodology for predictive inference when data distributions have general group symmetries in arbitrary observation models. Our methods leverage the novel notion of distributional equivariant transformations, which process the data while preserving their distributional invariances. We show that SymmPI has valid coverage under distributional invariance and characterize its performance under distribution shift, recovering recent results as special cases. We apply SymmPI to predict unobserved values associated to vertices in a network, where the distribution is unchanged under relabelings that keep the network structure unchanged. In several simulations in a two-layer hierarchical model, and in an empirical data analysis example, SymmPI performs favorably compared to existing methods.

Spectral Ranking Inferences based on General Multiway Comparisons

This paper studies the performance of the spectral method in the estimation and uncertainty quantification of the unobserved preference scores of compared entities in a very general and more realistic setup in which the comparison graph consists of hyper-edges of possible heterogeneous sizes and the number of comparisons can be as low as one for a given hyper-edge. Such a setting is pervasive in real applications, circumventing the need to specify the graph randomness and the restrictive homogeneous sampling assumption imposed in the commonly-used Bradley-Terry-Luce (BTL) or Plackett-Luce (PL) models. Furthermore, in the scenarios when the BTL or PL models are appropriate, we unravel the relationship between the spectral estimator and the Maximum Likelihood Estimator (MLE). We discover that a two-step spectral method, where we apply the optimal weighting estimated from the equal weighting vanilla spectral method, can achieve the same asymptotic efficiency as the MLE. Given the asymptotic distributions of the estimated preference scores, we also introduce a comprehensive framework to carry out both one-sample and two-sample ranking inferences, applicable to both fixed and random graph settings. It is noteworthy that it is the first time effective two-sample rank testing methods are proposed. Finally, we substantiate our findings via comprehensive numerical simulations and subsequently apply our developed methodologies to perform statistical inferences on statistics journals and movie rankings.

Uncertainty Quantification of MLE for Entity Ranking with Covariates

This paper concerns with statistical estimation and inference for the ranking problems based on pairwise comparisons with additional covariate information such as the attributes of the compared items. Despite extensive studies, few prior literatures investigate this problem under the more realistic setting where covariate information exists. To tackle this issue, we propose a novel model, Covariate-Assisted Ranking Estimation (CARE) model, that extends the well-known Bradley-Terry-Luce (BTL) model, by incorporating the covariate information. Specifically, instead of assuming every compared item has a fixed latent score $\{\theta_i^*\}_{i=1}^n$, we assume the underlying scores are given by $\{\alpha_i^*+{x}_i^\top\beta^*\}_{i=1}^n$, where $\alpha_i^*$ and ${x}_i^\top\beta^*$ represent latent baseline and covariate score of the $i$-th item, respectively. We impose natural identifiability conditions and derive the $\ell_{\infty}$- and $\ell_2$-optimal rates for the maximum likelihood estimator of $\{\alpha_i^*\}_{i=1}^{n}$ and $\beta^*$ under a sparse comparison graph, using a novel `leave-one-out' technique (Chen et al., 2019) . To conduct statistical inferences, we further derive asymptotic distributions for the MLE of $\{\alpha_i^*\}_{i=1}^n$ and $\beta^*$ with minimal sample complexity. This allows us to answer the question whether some covariates have any explanation power for latent scores and to threshold some sparse parameters to improve the ranking performance. We improve the approximation method used in (Gao et al., 2021) for the BLT model and generalize it to the CARE model. Moreover, we validate our theoretical results through large-scale numerical studies and an application to the mutual fund stock holding dataset.

Ranking Inferences Based on the Top Choice of Multiway Comparisons

This paper considers ranking inference of $n$ items based on the observed data on the top choice among $M$ randomly selected items at each trial. This is a useful modification of the Plackett-Luce model for $M$-way ranking with only the top choice observed and is an extension of the celebrated Bradley-Terry-Luce model that corresponds to $M=2$. Under a uniform sampling scheme in which any $M$ distinguished items are selected for comparisons with probability $p$ and the selected $M$ items are compared $L$ times with multinomial outcomes, we establish the statistical rates of convergence for underlying $n$ preference scores using both $\ell_2$-norm and $\ell_\infty$-norm, with the minimum sampling complexity. In addition, we establish the asymptotic normality of the maximum likelihood estimator that allows us to construct confidence intervals for the underlying scores. Furthermore, we propose a novel inference framework for ranking items through a sophisticated maximum pairwise difference statistic whose distribution is estimated via a valid Gaussian multiplier bootstrap. The estimated distribution is then used to construct simultaneous confidence intervals for the differences in the preference scores and the ranks of individual items. They also enable us to address various inference questions on the ranks of these items. Extensive simulation studies lend further support to our theoretical results. A real data application illustrates the usefulness of the proposed methods convincingly.

Robust High-dimensional Tuning Free Multiple Testing

A stylized feature of high-dimensional data is that many variables have heavy tails, and robust statistical inference is critical for valid large-scale statistical inference. Yet, the existing developments such as Winsorization, Huberization and median of means require the bounded second moments and involve variable-dependent tuning parameters, which hamper their fidelity in applications to large-scale problems. To liberate these constraints, this paper revisits the celebrated Hodges-Lehmann (HL) estimator for estimating location parameters in both the one- and two-sample problems, from a non-asymptotic perspective. Our study develops Berry-Esseen inequality and Cram\'{e}r type moderate deviation for the HL estimator based on newly developed non-asymptotic Bahadur representation, and builds data-driven confidence intervals via a weighted bootstrap approach. These results allow us to extend the HL estimator to large-scale studies and propose \emph{tuning-free} and \emph{moment-free} high-dimensional inference procedures for testing global null and for large-scale multiple testing with false discovery proportion control. It is convincingly shown that the resulting tuning-free and moment-free methods control false discovery proportion at a prescribed level. The simulation studies lend further support to our developed theory.

Strategic Decision-Making in the Presence of Information Asymmetry: Provably Efficient RL with Algorithmic Instruments

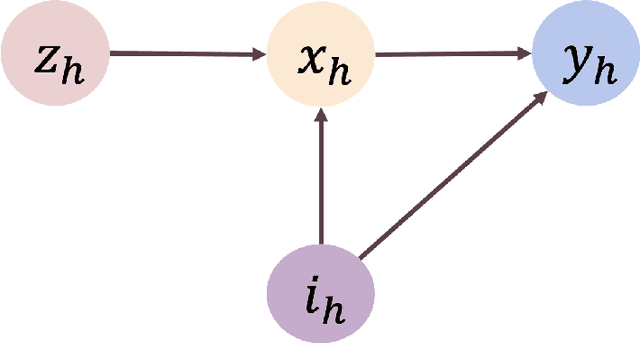
We study offline reinforcement learning under a novel model called strategic MDP, which characterizes the strategic interactions between a principal and a sequence of myopic agents with private types. Due to the bilevel structure and private types, strategic MDP involves information asymmetry between the principal and the agents. We focus on the offline RL problem, where the goal is to learn the optimal policy of the principal concerning a target population of agents based on a pre-collected dataset that consists of historical interactions. The unobserved private types confound such a dataset as they affect both the rewards and observations received by the principal. We propose a novel algorithm, Pessimistic policy Learning with Algorithmic iNstruments (PLAN), which leverages the ideas of instrumental variable regression and the pessimism principle to learn a near-optimal principal's policy in the context of general function approximation. Our algorithm is based on the critical observation that the principal's actions serve as valid instrumental variables. In particular, under a partial coverage assumption on the offline dataset, we prove that PLAN outputs a $1 / \sqrt{K}$-optimal policy with $K$ being the number of collected trajectories. We further apply our framework to some special cases of strategic MDP, including strategic regression, strategic bandit, and noncompliance in recommendation systems.

Are Latent Factor Regression and Sparse Regression Adequate?

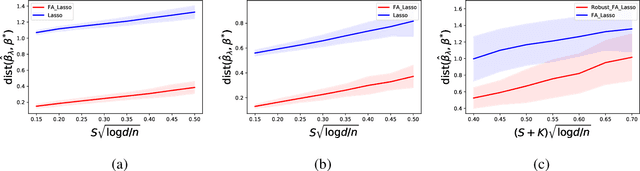
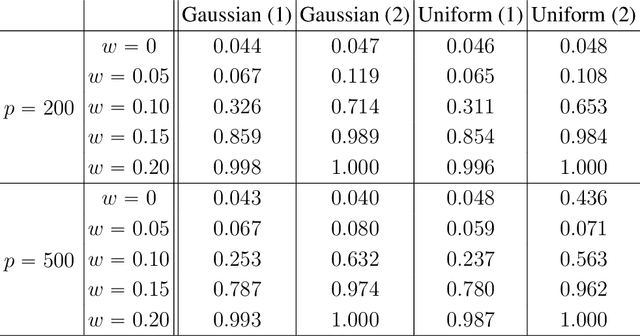
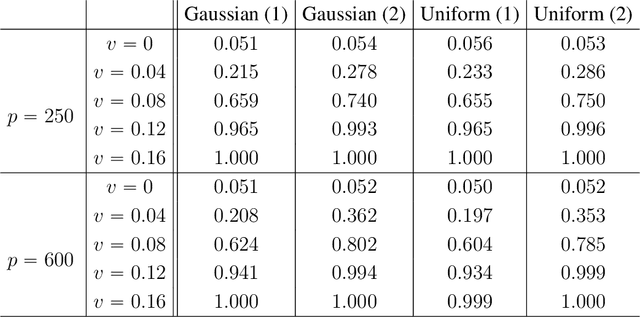
We propose the Factor Augmented sparse linear Regression Model (FARM) that not only encompasses both the latent factor regression and sparse linear regression as special cases but also bridges dimension reduction and sparse regression together. We provide theoretical guarantees for the estimation of our model under the existence of sub-Gaussian and heavy-tailed noises (with bounded (1+x)-th moment, for all x>0), respectively. In addition, the existing works on supervised learning often assume the latent factor regression or the sparse linear regression is the true underlying model without justifying its adequacy. To fill in such an important gap, we also leverage our model as the alternative model to test the sufficiency of the latent factor regression and the sparse linear regression models. To accomplish these goals, we propose the Factor-Adjusted de-Biased Test (FabTest) and a two-stage ANOVA type test respectively. We also conduct large-scale numerical experiments including both synthetic and FRED macroeconomics data to corroborate the theoretical properties of our methods. Numerical results illustrate the robustness and effectiveness of our model against latent factor regression and sparse linear regression models.

Policy Optimization Using Semiparametric Models for Dynamic Pricing

In this paper, we study the contextual dynamic pricing problem where the market value of a product is linear in its observed features plus some market noise. Products are sold one at a time, and only a binary response indicating success or failure of a sale is observed. Our model setting is similar to Javanmard and Nazerzadeh [2019] except that we expand the demand curve to a semiparametric model and need to learn dynamically both parametric and nonparametric components. We propose a dynamic statistical learning and decision-making policy that combines semiparametric estimation from a generalized linear model with an unknown link and online decision-making to minimize regret (maximize revenue). Under mild conditions, we show that for a market noise c.d.f. $F(\cdot)$ with $m$-th order derivative ($m\geq 2$), our policy achieves a regret upper bound of $\tilde{O}_{d}(T^{\frac{2m+1}{4m-1}})$, where $T$ is time horizon and $\tilde{O}_{d}$ is the order that hides logarithmic terms and the dimensionality of feature $d$. The upper bound is further reduced to $\tilde{O}_{d}(\sqrt{T})$ if $F$ is super smooth whose Fourier transform decays exponentially. In terms of dependence on the horizon $T$, these upper bounds are close to $\Omega(\sqrt{T})$, the lower bound where $F$ belongs to a parametric class. We further generalize these results to the case with dynamically dependent product features under the strong mixing condition.