ODELoRA: Training Low-Rank Adaptation by Solving Ordinary Differential Equations

Low-rank adaptation (LoRA) has emerged as a widely adopted parameter-efficient fine-tuning method in deep transfer learning, due to its reduced number of trainable parameters and lower memory requirements enabled by Burer-Monteiro factorization on adaptation matrices. However, classical LoRA training methods treat the low-rank factor matrices individually and optimize them using standard gradient-based algorithms. Such decoupled optimization schemes are theoretically and empirically suboptimal, as they fail to fully exploit the intrinsic structure of the LoRA parameterization. In this work, we propose a novel continuous-time optimization dynamic for LoRA factor matrices in the form of an ordinary differential equation (ODE) that emulates the gradient flow of full fine-tuning on the balanced manifold. We term this approach ODELoRA. To faithfully track the trajectories of ODELoRA, we adopt well-established and theoretically grounded time-discretization schemes, including Euler and Runge--Kutta methods. Our framework provides a unified ODE-based perspective for understanding and designing LoRA training algorithms. We establish linear convergence of the proposed method under strongly convex objectives for certain discretization schemes under mild conditions, and further extend our analysis to the matrix sensing setting. Moreover, we show that ODELoRA achieves stable feature learning, a property that is crucial for training deep neural networks at different scales of problem dimensionality. Empirical results on matrix sensing tasks confirm the derived linear convergence behavior, and experiments on training physics-informed neural networks further demonstrate the superiority of ODELoRA over existing baselines, especially in the training stability.

Almost Asymptotically Optimal Active Clustering Through Pairwise Observations

We propose a new analysis framework for clustering $M$ items into an unknown number of $K$ distinct groups using noisy and actively collected responses. At each time step, an agent is allowed to query pairs of items and observe bandit binary feedback. If the pair of items belongs to the same (resp.\ different) cluster, the observed feedback is $1$ with probability $p>1/2$ (resp.\ $q<1/2$). Leveraging the ubiquitous change-of-measure technique, we establish a fundamental lower bound on the expected number of queries needed to achieve a desired confidence in the clustering accuracy, formulated as a sup-inf optimization problem. Building on this theoretical foundation, we design an asymptotically optimal algorithm in which the stopping criterion involves an empirical version of the inner infimum -- the Generalized Likelihood Ratio (GLR) statistic -- being compared to a threshold. We develop a computationally feasible variant of the GLR statistic and show that its performance gap to the lower bound can be accurately empirically estimated and remains within a constant multiple of the lower bound.

Parameter-free Algorithms for the Stochastically Extended Adversarial Model

We develop the first parameter-free algorithms for the Stochastically Extended Adversarial (SEA) model, a framework that bridges adversarial and stochastic online convex optimization. Existing approaches for the SEA model require prior knowledge of problem-specific parameters, such as the diameter of the domain $D$ and the Lipschitz constant of the loss functions $G$, which limits their practical applicability. Addressing this, we develop parameter-free methods by leveraging the Optimistic Online Newton Step (OONS) algorithm to eliminate the need for these parameters. We first establish a comparator-adaptive algorithm for the scenario with unknown domain diameter but known Lipschitz constant, achieving an expected regret bound of $\tilde{O}\big(\|u\|_2^2 + \|u\|_2(\sqrt{\sigma^2_{1:T}} + \sqrt{\Sigma^2_{1:T}})\big)$, where $u$ is the comparator vector and $\sigma^2_{1:T}$ and $\Sigma^2_{1:T}$ represent the cumulative stochastic variance and cumulative adversarial variation, respectively. We then extend this to the more general setting where both $D$ and $G$ are unknown, attaining the comparator- and Lipschitz-adaptive algorithm. Notably, the regret bound exhibits the same dependence on $\sigma^2_{1:T}$ and $\Sigma^2_{1:T}$, demonstrating the efficacy of our proposed methods even when both parameters are unknown in the SEA model.

Automatic Rank Determination for Low-Rank Adaptation via Submodular Function Maximization

In this paper, we propose SubLoRA, a rank determination method for Low-Rank Adaptation (LoRA) based on submodular function maximization. In contrast to prior approaches, such as AdaLoRA, that rely on first-order (linearized) approximations of the loss function, SubLoRA utilizes second-order information to capture the potentially complex loss landscape by incorporating the Hessian matrix. We show that the linearization becomes inaccurate and ill-conditioned when the LoRA parameters have been well optimized, motivating the need for a more reliable and nuanced second-order formulation. To this end, we reformulate the rank determination problem as a combinatorial optimization problem with a quadratic objective. However, solving this problem exactly is NP-hard in general. To overcome the computational challenge, we introduce a submodular function maximization framework and devise a greedy algorithm with approximation guarantees. We derive a sufficient and necessary condition under which the rank-determination objective becomes submodular, and construct a closed-form projection of the Hessian matrix that satisfies this condition while maintaining computational efficiency. Our method combines solid theoretical foundations, second-order accuracy, and practical computational efficiency. We further extend SubLoRA to a joint optimization setting, alternating between LoRA parameter updates and rank determination under a rank budget constraint. Extensive experiments on fine-tuning physics-informed neural networks (PINNs) for solving partial differential equations (PDEs) demonstrate the effectiveness of our approach. Results show that SubLoRA outperforms existing methods in both rank determination and joint training performance.

Log-Sum-Exponential Estimator for Off-Policy Evaluation and Learning

Off-policy learning and evaluation leverage logged bandit feedback datasets, which contain context, action, propensity score, and feedback for each data point. These scenarios face significant challenges due to high variance and poor performance with low-quality propensity scores and heavy-tailed reward distributions. We address these issues by introducing a novel estimator based on the log-sum-exponential (LSE) operator, which outperforms traditional inverse propensity score estimators. Our LSE estimator demonstrates variance reduction and robustness under heavy-tailed conditions. For off-policy evaluation, we derive upper bounds on the estimator's bias and variance. In the off-policy learning scenario, we establish bounds on the regret -- the performance gap between our LSE estimator and the optimal policy -- assuming bounded $(1+\epsilon)$-th moment of weighted reward. Notably, we achieve a convergence rate of $O(n^{-\epsilon/(1+ \epsilon)})$ for the regret bounds, where $\epsilon \in [0,1]$ and $n$ is the size of logged bandit feedback dataset. Theoretical analysis is complemented by comprehensive empirical evaluations in both off-policy learning and evaluation scenarios, confirming the practical advantages of our approach. The code for our estimator is available at the following link: https://github.com/armin-behnamnia/lse-offpolicy-learning.

Best Arm Identification with Possibly Biased Offline Data

We study the best arm identification (BAI) problem with potentially biased offline data in the fixed confidence setting, which commonly arises in real-world scenarios such as clinical trials. We prove an impossibility result for adaptive algorithms without prior knowledge of the bias bound between online and offline distributions. To address this, we propose the LUCB-H algorithm, which introduces adaptive confidence bounds by incorporating an auxiliary bias correction to balance offline and online data within the LUCB framework. Theoretical analysis shows that LUCB-H matches the sample complexity of standard LUCB when offline data is misleading and significantly outperforms it when offline data is helpful. We also derive an instance-dependent lower bound that matches the upper bound of LUCB-H in certain scenarios. Numerical experiments further demonstrate the robustness and adaptability of LUCB-H in effectively incorporating offline data.

BanditSpec: Adaptive Speculative Decoding via Bandit Algorithms

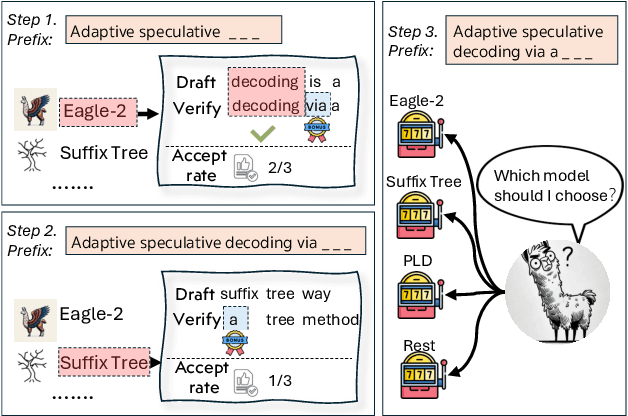
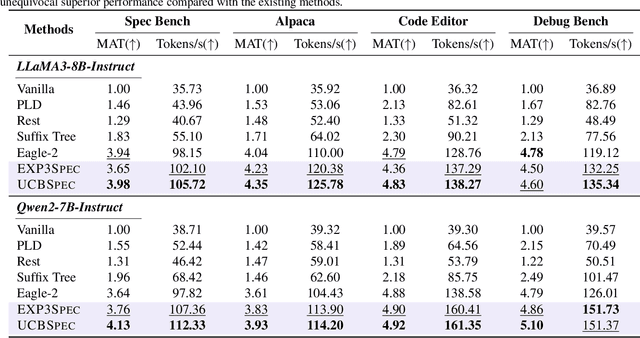
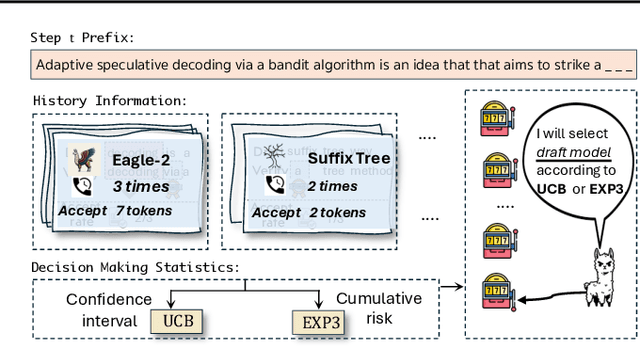
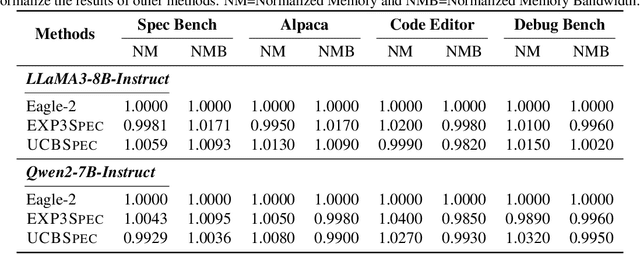
Speculative decoding has emerged as a popular method to accelerate the inference of Large Language Models (LLMs) while retaining their superior text generation performance. Previous methods either adopt a fixed speculative decoding configuration regardless of the prefix tokens, or train draft models in an offline or online manner to align them with the context. This paper proposes a training-free online learning framework to adaptively choose the configuration of the hyperparameters for speculative decoding as text is being generated. We first formulate this hyperparameter selection problem as a Multi-Armed Bandit problem and provide a general speculative decoding framework BanditSpec. Furthermore, two bandit-based hyperparameter selection algorithms, UCBSpec and EXP3Spec, are designed and analyzed in terms of a novel quantity, the stopping time regret. We upper bound this regret under both stochastic and adversarial reward settings. By deriving an information-theoretic impossibility result, it is shown that the regret performance of UCBSpec is optimal up to universal constants. Finally, extensive empirical experiments with LLaMA3 and Qwen2 demonstrate that our algorithms are effective compared to existing methods, and the throughput is close to the oracle best hyperparameter in simulated real-life LLM serving scenarios with diverse input prompts.

Low Tensor-Rank Adaptation of Kolmogorov--Arnold Networks

Kolmogorov--Arnold networks (KANs) have demonstrated their potential as an alternative to multi-layer perceptions (MLPs) in various domains, especially for science-related tasks. However, transfer learning of KANs remains a relatively unexplored area. In this paper, inspired by Tucker decomposition of tensors and evidence on the low tensor-rank structure in KAN parameter updates, we develop low tensor-rank adaptation (LoTRA) for fine-tuning KANs. We study the expressiveness of LoTRA based on Tucker decomposition approximations. Furthermore, we provide a theoretical analysis to select the learning rates for each LoTRA component to enable efficient training. Our analysis also shows that using identical learning rates across all components leads to inefficient training, highlighting the need for an adaptive learning rate strategy. Beyond theoretical insights, we explore the application of LoTRA for efficiently solving various partial differential equations (PDEs) by fine-tuning KANs. Additionally, we propose Slim KANs that incorporate the inherent low-tensor-rank properties of KAN parameter tensors to reduce model size while maintaining superior performance. Experimental results validate the efficacy of the proposed learning rate selection strategy and demonstrate the effectiveness of LoTRA for transfer learning of KANs in solving PDEs. Further evaluations on Slim KANs for function representation and image classification tasks highlight the expressiveness of LoTRA and the potential for parameter reduction through low tensor-rank decomposition.

Optimal Multi-Objective Best Arm Identification with Fixed Confidence

We consider a multi-armed bandit setting with finitely many arms, in which each arm yields an $M$-dimensional vector reward upon selection. We assume that the reward of each dimension (a.k.a. {\em objective}) is generated independently of the others. The best arm of any given objective is the arm with the largest component of mean corresponding to the objective. The end goal is to identify the best arm of {\em every} objective in the shortest (expected) time subject to an upper bound on the probability of error (i.e., fixed-confidence regime). We establish a problem-dependent lower bound on the limiting growth rate of the expected stopping time, in the limit of vanishing error probabilities. This lower bound, we show, is characterised by a max-min optimisation problem that is computationally expensive to solve at each time step. We propose an algorithm that uses the novel idea of {\em surrogate proportions} to sample the arms at each time step, eliminating the need to solve the max-min optimisation problem at each step. We demonstrate theoretically that our algorithm is asymptotically optimal. In addition, we provide extensive empirical studies to substantiate the efficiency of our algorithm. While existing works on pure exploration with multi-objective multi-armed bandits predominantly focus on {\em Pareto frontier identification}, our work fills the gap in the literature by conducting a formal investigation of the multi-objective best arm identification problem.

Enhancing Multi-Text Long Video Generation Consistency without Tuning: Time-Frequency Analysis, Prompt Alignment, and Theory

Despite the considerable progress achieved in the long video generation problem, there is still significant room to improve the consistency of the videos, particularly in terms of smoothness and transitions between scenes. We address these issues to enhance the consistency and coherence of videos generated with either single or multiple prompts. We propose the Time-frequency based temporal Attention Reweighting Algorithm (TiARA), which meticulously edits the attention score matrix based on the Discrete Short-Time Fourier Transform. Our method is supported by a theoretical guarantee, the first-of-its-kind for frequency-based methods in diffusion models. For videos generated by multiple prompts, we further investigate key factors affecting prompt interpolation quality and propose PromptBlend, an advanced prompt interpolation pipeline. The efficacy of our proposed method is validated via extensive experimental results, exhibiting consistent and impressive improvements over baseline methods. The code will be released upon acceptance.