Fast Tree-Field Integrators: From Low Displacement Rank to Topological Transformers

We present a new class of fast polylog-linear algorithms based on the theory of structured matrices (in particular low displacement rank) for integrating tensor fields defined on weighted trees. Several applications of the resulting fast tree-field integrators (FTFIs) are presented, including (a) approximation of graph metrics with tree metrics, (b) graph classification, (c) modeling on meshes, and finally (d) Topological Transformers (TTs) (Choromanski et al., 2022) for images. For Topological Transformers, we propose new relative position encoding (RPE) masking mechanisms with as few as three extra learnable parameters per Transformer layer, leading to 1.0-1.5%+ accuracy gains. Importantly, most of FTFIs are exact methods, thus numerically equivalent to their brute-force counterparts. When applied to graphs with thousands of nodes, those exact algorithms provide 5.7-13x speedups. We also provide an extensive theoretical analysis of our methods.

Hot PATE: Private Aggregation of Distributions for Diverse Task

The Private Aggregation of Teacher Ensembles (PATE) framework~\cite{PapernotAEGT:ICLR2017} is a versatile approach to privacy-preserving machine learning. In PATE, teacher models are trained on distinct portions of sensitive data, and their predictions are privately aggregated to label new training examples for a student model. Until now, PATE has primarily been explored with classification-like tasks, where each example possesses a ground-truth label, and knowledge is transferred to the student by labeling public examples. Generative AI models, however, excel in open ended \emph{diverse} tasks with multiple valid responses and scenarios that may not align with traditional labeled examples. Furthermore, the knowledge of models is often encapsulated in the response distribution itself and may be transferred from teachers to student in a more fluid way. We propose \emph{hot PATE}, tailored for the diverse setting. In hot PATE, each teacher model produces a response distribution and the aggregation method must preserve both privacy and diversity of responses. We demonstrate, analytically and empirically, that hot PATE achieves privacy-utility tradeoffs that are comparable to, and in diverse settings, significantly surpass, the baseline ``cold'' PATE.

SARA-RT: Scaling up Robotics Transformers with Self-Adaptive Robust Attention

We present Self-Adaptive Robust Attention for Robotics Transformers (SARA-RT): a new paradigm for addressing the emerging challenge of scaling up Robotics Transformers (RT) for on-robot deployment. SARA-RT relies on the new method of fine-tuning proposed by us, called up-training. It converts pre-trained or already fine-tuned Transformer-based robotic policies of quadratic time complexity (including massive billion-parameter vision-language-action models or VLAs), into their efficient linear-attention counterparts maintaining high quality. We demonstrate the effectiveness of SARA-RT by speeding up: (a) the class of recently introduced RT-2 models, the first VLA robotic policies pre-trained on internet-scale data, as well as (b) Point Cloud Transformer (PCT) robotic policies operating on large point clouds. We complement our results with the rigorous mathematical analysis providing deeper insight into the phenomenon of SARA.

Hardness of Low Rank Approximation of Entrywise Transformed Matrix Products

Inspired by fast algorithms in natural language processing, we study low rank approximation in the entrywise transformed setting where we want to find a good rank $k$ approximation to $f(U \cdot V)$, where $U, V^\top \in \mathbb{R}^{n \times r}$ are given, $r = O(\log(n))$, and $f(x)$ is a general scalar function. Previous work in sublinear low rank approximation has shown that if both (1) $U = V^\top$ and (2) $f(x)$ is a PSD kernel function, then there is an $O(nk^{\omega-1})$ time constant relative error approximation algorithm, where $\omega \approx 2.376$ is the exponent of matrix multiplication. We give the first conditional time hardness results for this problem, demonstrating that both conditions (1) and (2) are in fact necessary for getting better than $n^{2-o(1)}$ time for a relative error low rank approximation for a wide class of functions. We give novel reductions from the Strong Exponential Time Hypothesis (SETH) that rely on lower bounding the leverage scores of flat sparse vectors and hold even when the rank of the transformed matrix $f(UV)$ and the target rank are $n^{o(1)}$, and when $U = V^\top$. Furthermore, even when $f(x) = x^p$ is a simple polynomial, we give runtime lower bounds in the case when $U \neq V^\top$ of the form $\Omega(\min(n^{2-o(1)}, \Omega(2^p)))$. Lastly, we demonstrate that our lower bounds are tight by giving an $O(n \cdot \text{poly}(k, 2^p, 1/\epsilon))$ time relative error approximation algorithm and a fast $O(n \cdot \text{poly}(k, p, 1/\epsilon))$ additive error approximation using fast tensor-based sketching. Additionally, since our low rank algorithms rely on matrix-vector product subroutines, our lower bounds extend to show that computing $f(UV)W$, for even a small matrix $W$, requires $\Omega(n^{2-o(1)})$ time.

Efficient Graph Field Integrators Meet Point Clouds

We present two new classes of algorithms for efficient field integration on graphs encoding point clouds. The first class, SeparatorFactorization(SF), leverages the bounded genus of point cloud mesh graphs, while the second class, RFDiffusion(RFD), uses popular epsilon-nearest-neighbor graph representations for point clouds. Both can be viewed as providing the functionality of Fast Multipole Methods (FMMs), which have had a tremendous impact on efficient integration, but for non-Euclidean spaces. We focus on geometries induced by distributions of walk lengths between points (e.g., shortest-path distance). We provide an extensive theoretical analysis of our algorithms, obtaining new results in structural graph theory as a byproduct. We also perform exhaustive empirical evaluation, including on-surface interpolation for rigid and deformable objects (particularly for mesh-dynamics modeling), Wasserstein distance computations for point clouds, and the Gromov-Wasserstein variant.

Learning a Fourier Transform for Linear Relative Positional Encodings in Transformers

We propose a new class of linear Transformers called FourierLearner-Transformers (FLTs), which incorporate a wide range of relative positional encoding mechanisms (RPEs). These include regular RPE techniques applied for nongeometric data, as well as novel RPEs operating on the sequences of tokens embedded in higher-dimensional Euclidean spaces (e.g. point clouds). FLTs construct the optimal RPE mechanism implicitly by learning its spectral representation. As opposed to other architectures combining efficient low-rank linear attention with RPEs, FLTs remain practical in terms of their memory usage and do not require additional assumptions about the structure of the RPE-mask. FLTs allow also for applying certain structural inductive bias techniques to specify masking strategies, e.g. they provide a way to learn the so-called local RPEs introduced in this paper and providing accuracy gains as compared with several other linear Transformers for language modeling. We also thoroughly tested FLTs on other data modalities and tasks, such as: image classification and 3D molecular modeling. For 3D-data FLTs are, to the best of our knowledge, the first Transformers architectures providing RPE-enhanced linear attention.

FAVOR#: Sharp Attention Kernel Approximations via New Classes of Positive Random Features

The problem of efficient approximation of a linear operator induced by the Gaussian or softmax kernel is often addressed using random features (RFs) which yield an unbiased approximation of the operator's result. Such operators emerge in important applications ranging from kernel methods to efficient Transformers. We propose parameterized, positive, non-trigonometric RFs which approximate Gaussian and softmax-kernels. In contrast to traditional RF approximations, parameters of these new methods can be optimized to reduce the variance of the approximation, and the optimum can be expressed in closed form. We show that our methods lead to variance reduction in practice ($e^{10}$-times smaller variance and beyond) and outperform previous methods in a kernel regression task. Using our proposed mechanism, we also present FAVOR#, a method for self-attention approximation in Transformers. We show that FAVOR# outperforms other random feature methods in speech modelling and natural language processing.

Chefs' Random Tables: Non-Trigonometric Random Features

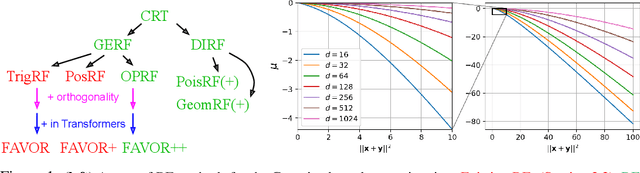
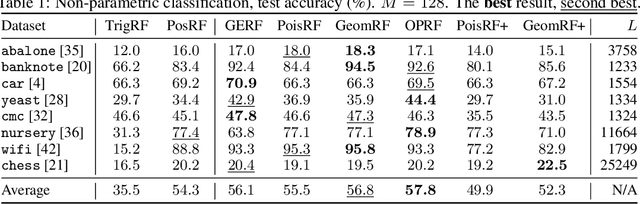
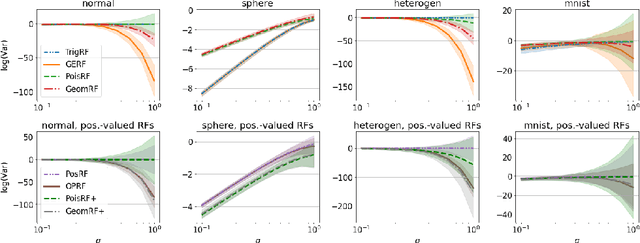
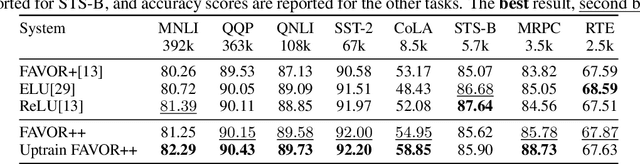
We introduce chefs' random tables (CRTs), a new class of non-trigonometric random features (RFs) to approximate Gaussian and softmax kernels. CRTs are an alternative to standard random kitchen sink (RKS) methods, which inherently rely on the trigonometric maps. We present variants of CRTs where RFs are positive, a key requirement for applications in recent low-rank Transformers. Further variance reduction is possible by leveraging statistics which are simple to compute. One instantiation of CRTs, the optimal positive random features (OPRFs), is to our knowledge the first RF method for unbiased softmax kernel estimation with positive and bounded RFs, resulting in exponentially small tails and much lower variance than its counterparts. As we show, orthogonal random features applied in OPRFs provide additional variance reduction for any dimensionality $d$ (not only asymptotically for sufficiently large $d$, as for RKS). We test CRTs on many tasks ranging from non-parametric classification to training Transformers for text, speech and image data, obtaining new state-of-the-art results for low-rank text Transformers, while providing linear space and time complexity.

ES-ENAS: Combining Evolution Strategies with Neural Architecture Search at No Extra Cost for Reinforcement Learning

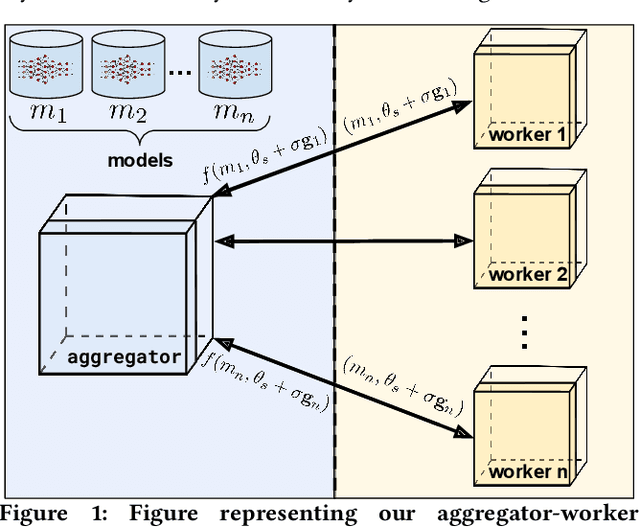
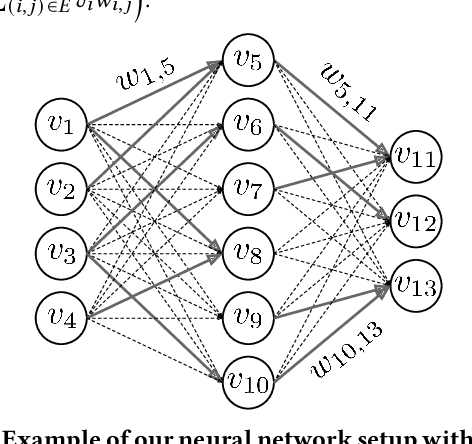
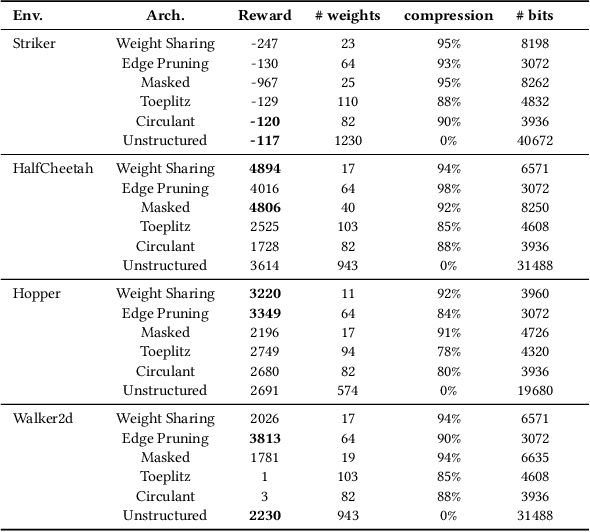
We introduce ES-ENAS, a simple neural architecture search (NAS) algorithm for the purpose of reinforcement learning (RL) policy design, by combining Evolutionary Strategies (ES) and Efficient NAS (ENAS) in a highly scalable and intuitive way. Our main insight is noticing that ES is already a distributed blackbox algorithm, and thus we may simply insert a model controller from ENAS into the central aggregator in ES and obtain weight sharing properties for free. By doing so, we bridge the gap from NAS research in supervised learning settings to the reinforcement learning scenario through this relatively simple marriage between two different lines of research, and are one of the first to apply controller-based NAS techniques to RL. We demonstrate the utility of our method by training combinatorial neural network architectures for RL problems in continuous control, via edge pruning and weight sharing. We also incorporate a wide variety of popular techniques from modern NAS literature, including multiobjective optimization and varying controller methods, to showcase their promise in the RL field and discuss possible extensions. We achieve >90% network compression for multiple tasks, which may be special interest in mobile robotics with limited storage and computational resources.

Differentially Private Weighted Sampling

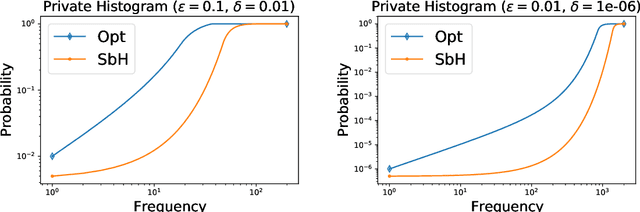
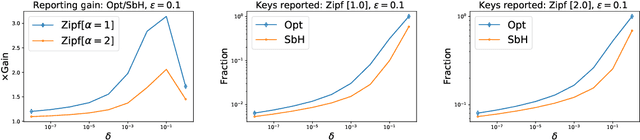
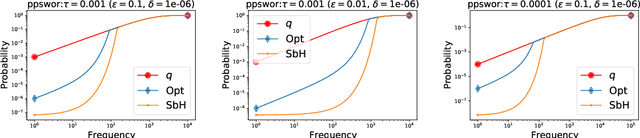
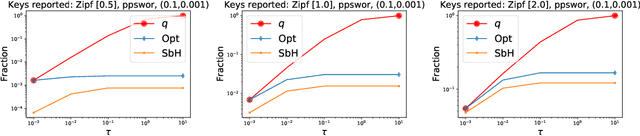
Common datasets have the form of {\em elements} with {\em keys} (e.g., transactions and products) and the goal is to perform analytics on the aggregated form of {\em key} and {\em frequency} pairs. A weighted sample of keys by (a function of) frequency is a highly versatile summary that provides a sparse set of representative keys and supports approximate evaluations of query statistics. We propose {\em private weighted sampling} (PWS): A method that ensures element-level differential privacy while retaining, to the extent possible, the utility of a respective non-private weighted sample. PWS maximizes the reporting probabilities of keys and improves over the state of the art also for the well-studied special case of {\em private histograms}, when no sampling is performed. We empirically demonstrate significant performance gains compared with prior baselines: 20\%-300\% increase in key reporting for common Zipfian frequency distributions and accuracy for $\times 2$-$ 8$ lower frequencies in estimation tasks. Moreover, PWS is applied as a simple post-processing of a non-private sample, without requiring the original data. This allows for seamless integration with existing implementations of non-private schemes and retaining the efficiency of schemes designed for resource-constrained settings such as massive distributed or streamed data. We believe that due to practicality and performance, PWS may become a method of choice in applications where privacy is desired.