Scaling Embedding Layers in Language Models

We propose SCONE ($\textbf{S}$calable, $\textbf{C}$ontextualized, $\textbf{O}$ffloaded, $\textbf{N}$-gram $\textbf{E}$mbedding), a method for extending input embedding layers to enhance language model performance as layer size scales. To avoid increased decoding costs, SCONE retains the original vocabulary while introducing embeddings for a set of frequent $n$-grams. These embeddings provide contextualized representation for each input token and are learned with a separate model during training. During inference, they are precomputed and stored in off-accelerator memory with minimal impact on inference speed. SCONE enables two new scaling strategies: increasing the number of cached $n$-gram embeddings and scaling the model used to learn them, all while maintaining fixed inference-time FLOPS. We show that scaling both aspects allows SCONE to outperform a 1.9B parameter baseline across diverse corpora, while using only half the inference-time FLOPS.

Lower Bounds for Differential Privacy Under Continual Observation and Online Threshold Queries

One of the most basic problems for studying the "price of privacy over time" is the so called private counter problem, introduced by Dwork et al. (2010) and Chan et al. (2010). In this problem, we aim to track the number of events that occur over time, while hiding the existence of every single event. More specifically, in every time step $t\in[T]$ we learn (in an online fashion) that $\Delta_t\geq 0$ new events have occurred, and must respond with an estimate $n_t\approx\sum_{j=1}^t \Delta_j$. The privacy requirement is that all of the outputs together, across all time steps, satisfy event level differential privacy. The main question here is how our error needs to depend on the total number of time steps $T$ and the total number of events $n$. Dwork et al. (2015) showed an upper bound of $O\left(\log(T)+\log^2(n)\right)$, and Henzinger et al. (2023) showed a lower bound of $\Omega\left(\min\{\log n, \log T\}\right)$. We show a new lower bound of $\Omega\left(\min\{n,\log T\}\right)$, which is tight w.r.t. the dependence on $T$, and is tight in the sparse case where $\log^2 n=O(\log T)$. Our lower bound has the following implications: $\bullet$ We show that our lower bound extends to the "online thresholds problem", where the goal is to privately answer many "quantile queries" when these queries are presented one-by-one. This resolves an open question of Bun et al. (2017). $\bullet$ Our lower bound implies, for the first time, a separation between the number of mistakes obtainable by a private online learner and a non-private online learner. This partially resolves a COLT'22 open question published by Sanyal and Ramponi. $\bullet$ Our lower bound also yields the first separation between the standard model of private online learning and a recently proposed relaxed variant of it, called private online prediction.

Hot PATE: Private Aggregation of Distributions for Diverse Task

The Private Aggregation of Teacher Ensembles (PATE) framework~\cite{PapernotAEGT:ICLR2017} is a versatile approach to privacy-preserving machine learning. In PATE, teacher models are trained on distinct portions of sensitive data, and their predictions are privately aggregated to label new training examples for a student model. Until now, PATE has primarily been explored with classification-like tasks, where each example possesses a ground-truth label, and knowledge is transferred to the student by labeling public examples. Generative AI models, however, excel in open ended \emph{diverse} tasks with multiple valid responses and scenarios that may not align with traditional labeled examples. Furthermore, the knowledge of models is often encapsulated in the response distribution itself and may be transferred from teachers to student in a more fluid way. We propose \emph{hot PATE}, tailored for the diverse setting. In hot PATE, each teacher model produces a response distribution and the aggregation method must preserve both privacy and diversity of responses. We demonstrate, analytically and empirically, that hot PATE achieves privacy-utility tradeoffs that are comparable to, and in diverse settings, significantly surpass, the baseline ``cold'' PATE.

Õptimal Differentially Private Learning of Thresholds and Quasi-Concave Optimization

The problem of learning threshold functions is a fundamental one in machine learning. Classical learning theory implies sample complexity of $O(\xi^{-1} \log(1/\beta))$ (for generalization error $\xi$ with confidence $1-\beta$). The private version of the problem, however, is more challenging and in particular, the sample complexity must depend on the size $|X|$ of the domain. Progress on quantifying this dependence, via lower and upper bounds, was made in a line of works over the past decade. In this paper, we finally close the gap for approximate-DP and provide a nearly tight upper bound of $\tilde{O}(\log^* |X|)$, which matches a lower bound by Alon et al (that applies even with improper learning) and improves over a prior upper bound of $\tilde{O}((\log^* |X|)^{1.5})$ by Kaplan et al. We also provide matching upper and lower bounds of $\tilde{\Theta}(2^{\log^*|X|})$ for the additive error of private quasi-concave optimization (a related and more general problem). Our improvement is achieved via the novel Reorder-Slice-Compute paradigm for private data analysis which we believe will have further applications.

Tricking the Hashing Trick: A Tight Lower Bound on the Robustness of CountSketch to Adaptive Inputs

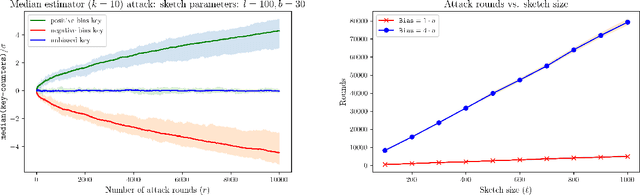
CountSketch and Feature Hashing (the "hashing trick") are popular randomized dimensionality reduction methods that support recovery of $\ell_2$-heavy hitters (keys $i$ where $v_i^2 > \epsilon \|\boldsymbol{v}\|_2^2$) and approximate inner products. When the inputs are {\em not adaptive} (do not depend on prior outputs), classic estimators applied to a sketch of size $O(\ell/\epsilon)$ are accurate for a number of queries that is exponential in $\ell$. When inputs are adaptive, however, an adversarial input can be constructed after $O(\ell)$ queries with the classic estimator and the best known robust estimator only supports $\tilde{O}(\ell^2)$ queries. In this work we show that this quadratic dependence is in a sense inherent: We design an attack that after $O(\ell^2)$ queries produces an adversarial input vector whose sketch is highly biased. Our attack uses "natural" non-adaptive inputs (only the final adversarial input is chosen adaptively) and universally applies with any correct estimator, including one that is unknown to the attacker. In that, we expose inherent vulnerability of this fundamental method.

On the Robustness of CountSketch to Adaptive Inputs

CountSketch is a popular dimensionality reduction technique that maps vectors to a lower dimension using randomized linear measurements. The sketch supports recovering $\ell_2$-heavy hitters of a vector (entries with $v[i]^2 \geq \frac{1}{k}\|\boldsymbol{v}\|^2_2$). We study the robustness of the sketch in adaptive settings where input vectors may depend on the output from prior inputs. Adaptive settings arise in processes with feedback or with adversarial attacks. We show that the classic estimator is not robust, and can be attacked with a number of queries of the order of the sketch size. We propose a robust estimator (for a slightly modified sketch) that allows for quadratic number of queries in the sketch size, which is an improvement factor of $\sqrt{k}$ (for $k$ heavy hitters) over prior work.

Differentially-Private Clustering of Easy Instances

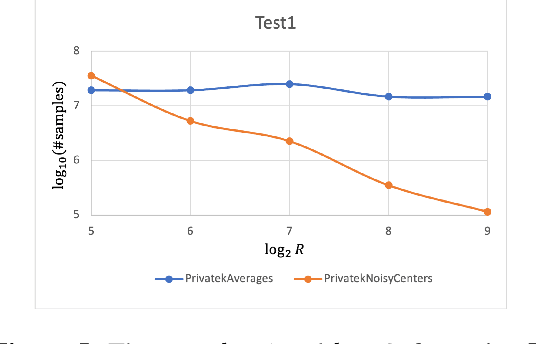
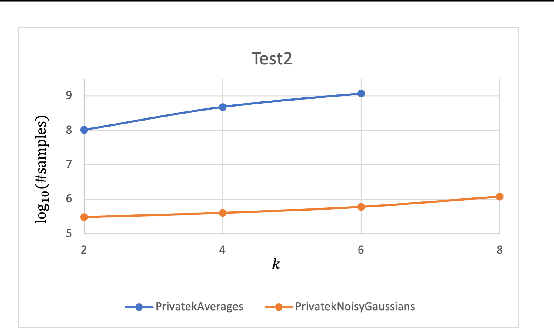
Clustering is a fundamental problem in data analysis. In differentially private clustering, the goal is to identify $k$ cluster centers without disclosing information on individual data points. Despite significant research progress, the problem had so far resisted practical solutions. In this work we aim at providing simple implementable differentially private clustering algorithms that provide utility when the data is "easy," e.g., when there exists a significant separation between the clusters. We propose a framework that allows us to apply non-private clustering algorithms to the easy instances and privately combine the results. We are able to get improved sample complexity bounds in some cases of Gaussian mixtures and $k$-means. We complement our theoretical analysis with an empirical evaluation on synthetic data.

FriendlyCore: Practical Differentially Private Aggregation

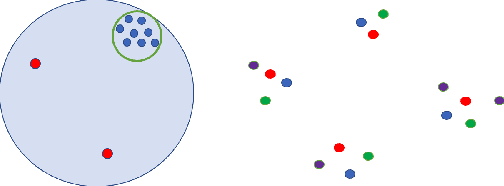
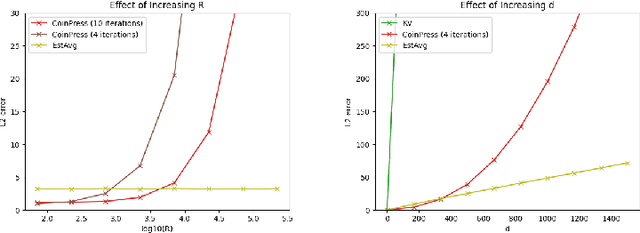
Differentially private algorithms for common metric aggregation tasks, such as clustering or averaging, often have limited practicality due to their complexity or a large number of data points that is required for accurate results. We propose a simple and practical tool $\mathsf{FriendlyCore}$ that takes a set of points ${\cal D}$ from an unrestricted (pseudo) metric space as input. When ${\cal D}$ has effective diameter $r$, $\mathsf{FriendlyCore}$ returns a "stable" subset ${\cal D}_G\subseteq {\cal D}$ that includes all points, except possibly few outliers, and is {\em certified} to have diameter $r$. $\mathsf{FriendlyCore}$ can be used to preprocess the input before privately aggregating it, potentially simplifying the aggregation or boosting its accuracy. Surprisingly, $\mathsf{FriendlyCore}$ is light-weight with no dependence on the dimension. We empirically demonstrate its advantages in boosting the accuracy of mean estimation, outperforming tailored methods.

A Framework for Adversarial Streaming via Differential Privacy and Difference Estimators

Streaming algorithms are algorithms for processing large data streams, using only a limited amount of memory. Classical streaming algorithms operate under the assumption that the input stream is fixed in advance. Recently, there is a growing interest in studying streaming algorithms that provide provable guarantees even when the input stream is chosen by an adaptive adversary. Such streaming algorithms are said to be {\em adversarially-robust}. We propose a novel framework for adversarial streaming that hybrids two recently suggested frameworks by Hassidim et al. (2020) and by Woodruff and Zhou (2021). These recently suggested frameworks rely on very different ideas, each with its own strengths and weaknesses. We combine these two frameworks (in a non-trivial way) into a single hybrid framework that gains from both approaches to obtain superior performances for turnstile streams.

Differentially Private Weighted Sampling

Common datasets have the form of {\em elements} with {\em keys} (e.g., transactions and products) and the goal is to perform analytics on the aggregated form of {\em key} and {\em frequency} pairs. A weighted sample of keys by (a function of) frequency is a highly versatile summary that provides a sparse set of representative keys and supports approximate evaluations of query statistics. We propose {\em private weighted sampling} (PWS): A method that ensures element-level differential privacy while retaining, to the extent possible, the utility of a respective non-private weighted sample. PWS maximizes the reporting probabilities of keys and improves over the state of the art also for the well-studied special case of {\em private histograms}, when no sampling is performed. We empirically demonstrate significant performance gains compared with prior baselines: 20\%-300\% increase in key reporting for common Zipfian frequency distributions and accuracy for $\times 2$-$ 8$ lower frequencies in estimation tasks. Moreover, PWS is applied as a simple post-processing of a non-private sample, without requiring the original data. This allows for seamless integration with existing implementations of non-private schemes and retaining the efficiency of schemes designed for resource-constrained settings such as massive distributed or streamed data. We believe that due to practicality and performance, PWS may become a method of choice in applications where privacy is desired.