Communication Bounds for the Distributed Experts Problem

In this work, we study the experts problem in the distributed setting where an expert's cost needs to be aggregated across multiple servers. Our study considers various communication models such as the message-passing model and the broadcast model, along with multiple aggregation functions, such as summing and taking the $\ell_p$ norm of an expert's cost across servers. We propose the first communication-efficient protocols that achieve near-optimal regret in these settings, even against a strong adversary who can choose the inputs adaptively. Additionally, we give a conditional lower bound showing that the communication of our protocols is nearly optimal. Finally, we implement our protocols and demonstrate empirical savings on the HPO-B benchmarks.

Even Sparser Graph Transformers

Graph Transformers excel in long-range dependency modeling, but generally require quadratic memory complexity in the number of nodes in an input graph, and hence have trouble scaling to large graphs. Sparse attention variants such as Exphormer can help, but may require high-degree augmentations to the input graph for good performance, and do not attempt to sparsify an already-dense input graph. As the learned attention mechanisms tend to use few of these edges, such high-degree connections may be unnecessary. We show (empirically and with theoretical backing) that attention scores on graphs are usually quite consistent across network widths, and use this observation to propose a two-stage procedure, which we call Spexphormer: first, train a narrow network on the full augmented graph. Next, use only the active connections to train a wider network on a much sparser graph. We establish theoretical conditions when a narrow network's attention scores can match those of a wide network, and show that Spexphormer achieves good performance with drastically reduced memory requirements on various graph datasets.

A Theory for Compressibility of Graph Transformers for Transductive Learning

Transductive tasks on graphs differ fundamentally from typical supervised machine learning tasks, as the independent and identically distributed (i.i.d.) assumption does not hold among samples. Instead, all train/test/validation samples are present during training, making them more akin to a semi-supervised task. These differences make the analysis of the models substantially different from other models. Recently, Graph Transformers have significantly improved results on these datasets by overcoming long-range dependency problems. However, the quadratic complexity of full Transformers has driven the community to explore more efficient variants, such as those with sparser attention patterns. While the attention matrix has been extensively discussed, the hidden dimension or width of the network has received less attention. In this work, we establish some theoretical bounds on how and under what conditions the hidden dimension of these networks can be compressed. Our results apply to both sparse and dense variants of Graph Transformers.

Grass: Compute Efficient Low-Memory LLM Training with Structured Sparse Gradients

Large language model (LLM) training and finetuning are often bottlenecked by limited GPU memory. While existing projection-based optimization methods address this by projecting gradients into a lower-dimensional subspace to reduce optimizer state memory, they typically rely on dense projection matrices, which can introduce computational and memory overheads. In this work, we propose Grass (GRAdient Stuctured Sparsification), a novel approach that leverages sparse projections to transform gradients into structured sparse updates. This design not only significantly reduces memory usage for optimizer states but also minimizes gradient memory footprint, computation, and communication costs, leading to substantial throughput improvements. Extensive experiments on pretraining and finetuning tasks demonstrate that Grass achieves competitive performance to full-rank training and existing projection-based methods. Notably, Grass enables half-precision pretraining of a 13B parameter LLaMA model on a single 40GB A100 GPU--a feat infeasible for previous methods--and yields up to a $2\times$ throughput improvement on an 8-GPU system. Code can be found at https://github.com/aashiqmuhamed/GRASS .

Data-Efficient Learning via Clustering-Based Sensitivity Sampling: Foundation Models and Beyond

We study the data selection problem, whose aim is to select a small representative subset of data that can be used to efficiently train a machine learning model. We present a new data selection approach based on $k$-means clustering and sensitivity sampling. Assuming access to an embedding representation of the data with respect to which the model loss is H\"older continuous, our approach provably allows selecting a set of ``typical'' $k + 1/\varepsilon^2$ elements whose average loss corresponds to the average loss of the whole dataset, up to a multiplicative $(1\pm\varepsilon)$ factor and an additive $\varepsilon \lambda \Phi_k$, where $\Phi_k$ represents the $k$-means cost for the input embeddings and $\lambda$ is the H\"older constant. We furthermore demonstrate the performance and scalability of our approach on fine-tuning foundation models and show that it outperforms state-of-the-art methods. We also show how it can be applied on linear regression, leading to a new sampling strategy that surprisingly matches the performances of leverage score sampling, while being conceptually simpler and more scalable.

Adaptive Regret for Bandits Made Possible: Two Queries Suffice

Fast changing states or volatile environments pose a significant challenge to online optimization, which needs to perform rapid adaptation under limited observation. In this paper, we give query and regret optimal bandit algorithms under the strict notion of strongly adaptive regret, which measures the maximum regret over any contiguous interval $I$. Due to its worst-case nature, there is an almost-linear $\Omega(|I|^{1-\epsilon})$ regret lower bound, when only one query per round is allowed [Daniely el al, ICML 2015]. Surprisingly, with just two queries per round, we give Strongly Adaptive Bandit Learner (StABL) that achieves $\tilde{O}(\sqrt{n|I|})$ adaptive regret for multi-armed bandits with $n$ arms. The bound is tight and cannot be improved in general. Our algorithm leverages a multiplicative update scheme of varying stepsizes and a carefully chosen observation distribution to control the variance. Furthermore, we extend our results and provide optimal algorithms in the bandit convex optimization setting. Finally, we empirically demonstrate the superior performance of our algorithms under volatile environments and for downstream tasks, such as algorithm selection for hyperparameter optimization.

Hardness of Low Rank Approximation of Entrywise Transformed Matrix Products

Inspired by fast algorithms in natural language processing, we study low rank approximation in the entrywise transformed setting where we want to find a good rank $k$ approximation to $f(U \cdot V)$, where $U, V^\top \in \mathbb{R}^{n \times r}$ are given, $r = O(\log(n))$, and $f(x)$ is a general scalar function. Previous work in sublinear low rank approximation has shown that if both (1) $U = V^\top$ and (2) $f(x)$ is a PSD kernel function, then there is an $O(nk^{\omega-1})$ time constant relative error approximation algorithm, where $\omega \approx 2.376$ is the exponent of matrix multiplication. We give the first conditional time hardness results for this problem, demonstrating that both conditions (1) and (2) are in fact necessary for getting better than $n^{2-o(1)}$ time for a relative error low rank approximation for a wide class of functions. We give novel reductions from the Strong Exponential Time Hypothesis (SETH) that rely on lower bounding the leverage scores of flat sparse vectors and hold even when the rank of the transformed matrix $f(UV)$ and the target rank are $n^{o(1)}$, and when $U = V^\top$. Furthermore, even when $f(x) = x^p$ is a simple polynomial, we give runtime lower bounds in the case when $U \neq V^\top$ of the form $\Omega(\min(n^{2-o(1)}, \Omega(2^p)))$. Lastly, we demonstrate that our lower bounds are tight by giving an $O(n \cdot \text{poly}(k, 2^p, 1/\epsilon))$ time relative error approximation algorithm and a fast $O(n \cdot \text{poly}(k, p, 1/\epsilon))$ additive error approximation using fast tensor-based sketching. Additionally, since our low rank algorithms rely on matrix-vector product subroutines, our lower bounds extend to show that computing $f(UV)W$, for even a small matrix $W$, requires $\Omega(n^{2-o(1)})$ time.

Almost Linear Constant-Factor Sketching for $\ell_1$ and Logistic Regression

We improve upon previous oblivious sketching and turnstile streaming results for $\ell_1$ and logistic regression, giving a much smaller sketching dimension achieving $O(1)$-approximation and yielding an efficient optimization problem in the sketch space. Namely, we achieve for any constant $c>0$ a sketching dimension of $\tilde{O}(d^{1+c})$ for $\ell_1$ regression and $\tilde{O}(\mu d^{1+c})$ for logistic regression, where $\mu$ is a standard measure that captures the complexity of compressing the data. For $\ell_1$-regression our sketching dimension is near-linear and improves previous work which either required $\Omega(\log d)$-approximation with this sketching dimension, or required a larger $\operatorname{poly}(d)$ number of rows. Similarly, for logistic regression previous work had worse $\operatorname{poly}(\mu d)$ factors in its sketching dimension. We also give a tradeoff that yields a $1+\varepsilon$ approximation in input sparsity time by increasing the total size to $(d\log(n)/\varepsilon)^{O(1/\varepsilon)}$ for $\ell_1$ and to $(\mu d\log(n)/\varepsilon)^{O(1/\varepsilon)}$ for logistic regression. Finally, we show that our sketch can be extended to approximate a regularized version of logistic regression where the data-dependent regularizer corresponds to the variance of the individual logistic losses.

Oblivious sketching for logistic regression

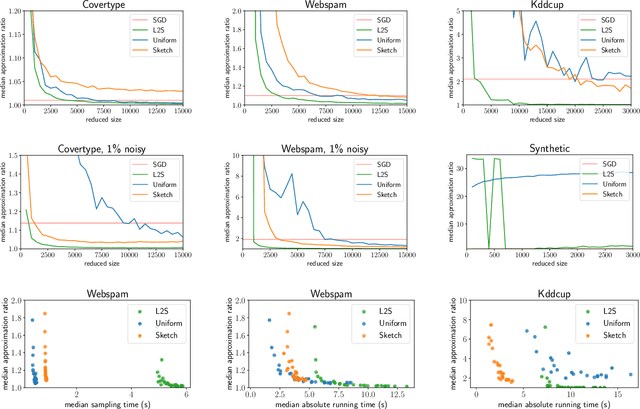
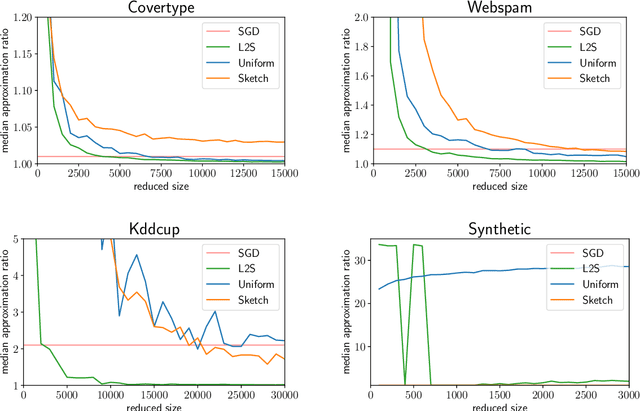
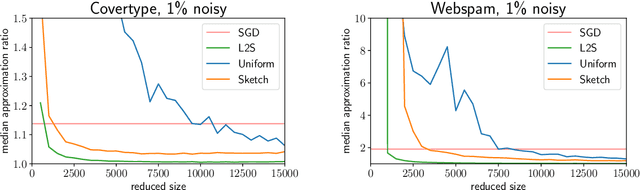
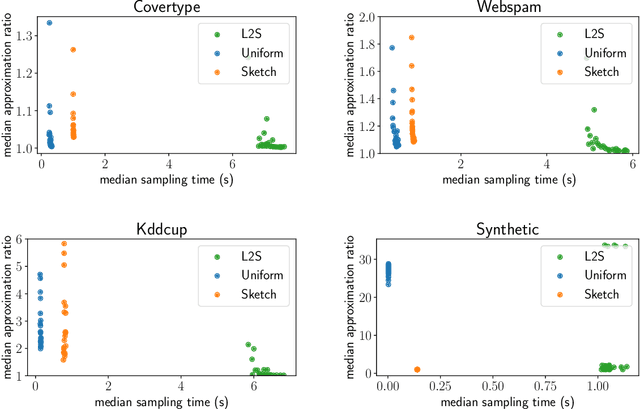
What guarantees are possible for solving logistic regression in one pass over a data stream? To answer this question, we present the first data oblivious sketch for logistic regression. Our sketch can be computed in input sparsity time over a turnstile data stream and reduces the size of a $d$-dimensional data set from $n$ to only $\operatorname{poly}(\mu d\log n)$ weighted points, where $\mu$ is a useful parameter which captures the complexity of compressing the data. Solving (weighted) logistic regression on the sketch gives an $O(\log n)$-approximation to the original problem on the full data set. We also show how to obtain an $O(1)$-approximation with slight modifications. Our sketches are fast, simple, easy to implement, and our experiments demonstrate their practicality.

Regularized Weighted Low Rank Approximation

The classical low rank approximation problem is to find a rank $k$ matrix $UV$ (where $U$ has $k$ columns and $V$ has $k$ rows) that minimizes the Frobenius norm of $A - UV$. Although this problem can be solved efficiently, we study an NP-hard variant of this problem that involves weights and regularization. A previous paper of [Razenshteyn et al. '16] derived a polynomial time algorithm for weighted low rank approximation with constant rank. We derive provably sharper guarantees for the regularized version by obtaining parameterized complexity bounds in terms of the statistical dimension rather than the rank, allowing for a rank-independent runtime that can be significantly faster. Our improvement comes from applying sharper matrix concentration bounds, using a novel conditioning technique, and proving structural theorems for regularized low rank problems.