A Comprehensive Survey of Graph-level Learning

Graphs have a superior ability to represent relational data, like chemical compounds, proteins, and social networks. Hence, graph-level learning, which takes a set of graphs as input, has been applied to many tasks including comparison, regression, classification, and more. Traditional approaches to learning a set of graphs tend to rely on hand-crafted features, such as substructures. But while these methods benefit from good interpretability, they often suffer from computational bottlenecks as they cannot skirt the graph isomorphism problem. Conversely, deep learning has helped graph-level learning adapt to the growing scale of graphs by extracting features automatically and decoding graphs into low-dimensional representations. As a result, these deep graph learning methods have been responsible for many successes. Yet, there is no comprehensive survey that reviews graph-level learning starting with traditional learning and moving through to the deep learning approaches. This article fills this gap and frames the representative algorithms into a systematic taxonomy covering traditional learning, graph-level deep neural networks, graph-level graph neural networks, and graph pooling. To ensure a thoroughly comprehensive survey, the evolutions, interactions, and communications between methods from four different branches of development are also examined. This is followed by a brief review of the benchmark data sets, evaluation metrics, and common downstream applications. The survey concludes with 13 future directions of necessary research that will help to overcome the challenges facing this booming field.

DAGAD: Data Augmentation for Graph Anomaly Detection

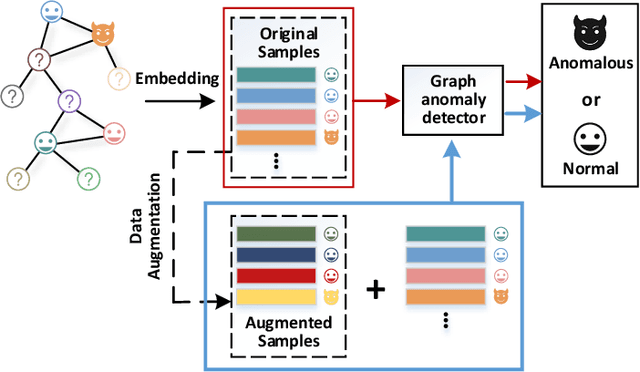
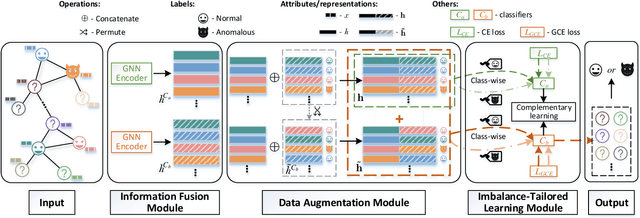
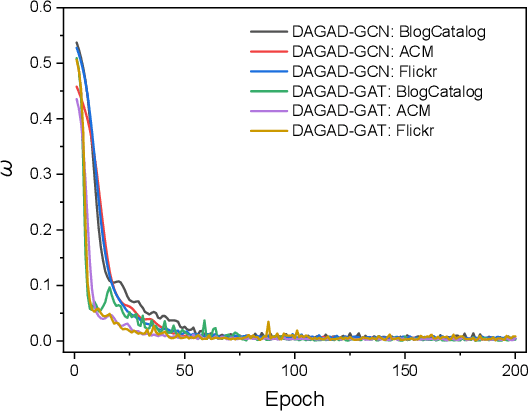
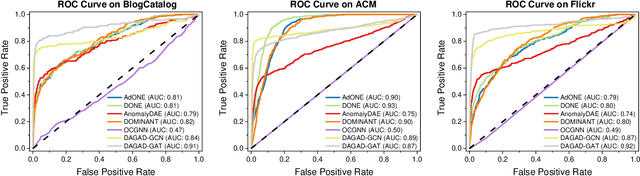
Graph anomaly detection in this paper aims to distinguish abnormal nodes that behave differently from the benign ones accounting for the majority of graph-structured instances. Receiving increasing attention from both academia and industry, yet existing research on this task still suffers from two critical issues when learning informative anomalous behavior from graph data. For one thing, anomalies are usually hard to capture because of their subtle abnormal behavior and the shortage of background knowledge about them, which causes severe anomalous sample scarcity. Meanwhile, the overwhelming majority of objects in real-world graphs are normal, bringing the class imbalance problem as well. To bridge the gaps, this paper devises a novel Data Augmentation-based Graph Anomaly Detection (DAGAD) framework for attributed graphs, equipped with three specially designed modules: 1) an information fusion module employing graph neural network encoders to learn representations, 2) a graph data augmentation module that fertilizes the training set with generated samples, and 3) an imbalance-tailored learning module to discriminate the distributions of the minority (anomalous) and majority (normal) classes. A series of experiments on three datasets prove that DAGAD outperforms ten state-of-the-art baseline detectors concerning various mostly-used metrics, together with an extensive ablation study validating the strength of our proposed modules.

Geometry Contrastive Learning on Heterogeneous Graphs

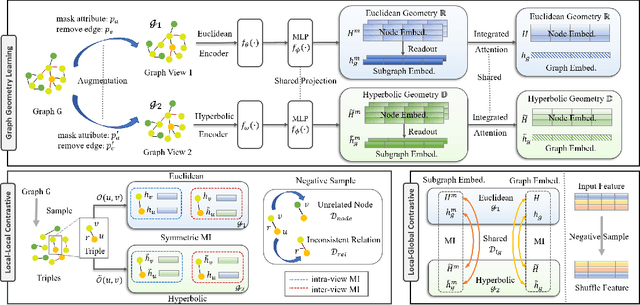
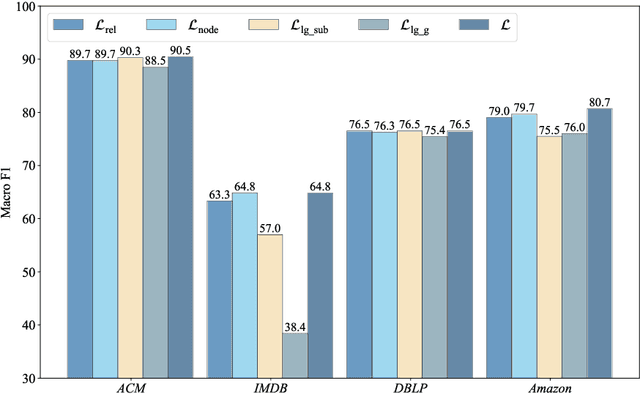
Self-supervised learning (especially contrastive learning) methods on heterogeneous graphs can effectively get rid of the dependence on supervisory data. Meanwhile, most existing representation learning methods embed the heterogeneous graphs into a single geometric space, either Euclidean or hyperbolic. This kind of single geometric view is usually not enough to observe the complete picture of heterogeneous graphs due to their rich semantics and complex structures. Under these observations, this paper proposes a novel self-supervised learning method, termed as Geometry Contrastive Learning (GCL), to better represent the heterogeneous graphs when supervisory data is unavailable. GCL views a heterogeneous graph from Euclidean and hyperbolic perspective simultaneously, aiming to make a strong merger of the ability of modeling rich semantics and complex structures, which is expected to bring in more benefits for downstream tasks. GCL maximizes the mutual information between two geometric views by contrasting representations at both local-local and local-global semantic levels. Extensive experiments on four benchmarks data sets show that the proposed approach outperforms the strong baselines, including both unsupervised methods and supervised methods, on three tasks, including node classification, node clustering and similarity search.

Ultrahyperbolic Knowledge Graph Embeddings

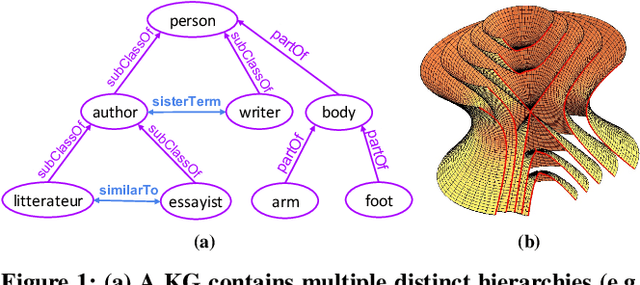
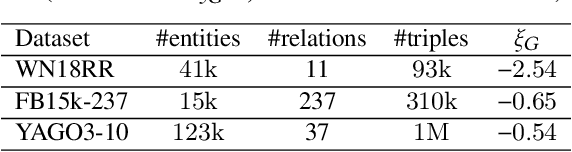
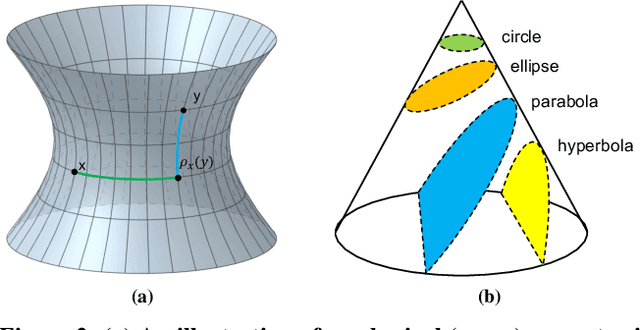
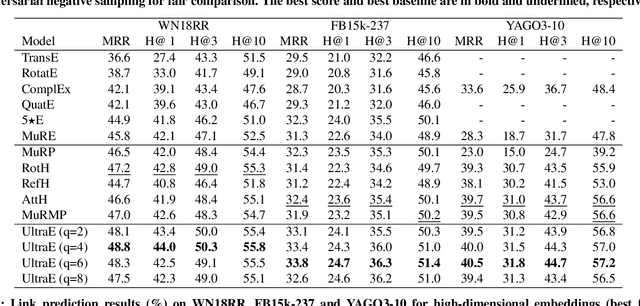
Recent knowledge graph (KG) embeddings have been advanced by hyperbolic geometry due to its superior capability for representing hierarchies. The topological structures of real-world KGs, however, are rather heterogeneous, i.e., a KG is composed of multiple distinct hierarchies and non-hierarchical graph structures. Therefore, a homogeneous (either Euclidean or hyperbolic) geometry is not sufficient for fairly representing such heterogeneous structures. To capture the topological heterogeneity of KGs, we present an ultrahyperbolic KG embedding (UltraE) in an ultrahyperbolic (or pseudo-Riemannian) manifold that seamlessly interleaves hyperbolic and spherical manifolds. In particular, we model each relation as a pseudo-orthogonal transformation that preserves the pseudo-Riemannian bilinear form. The pseudo-orthogonal transformation is decomposed into various operators (i.e., circular rotations, reflections and hyperbolic rotations), allowing for simultaneously modeling heterogeneous structures as well as complex relational patterns. Experimental results on three standard KGs show that UltraE outperforms previous Euclidean- and hyperbolic-based approaches.

Graph-level Neural Networks: Current Progress and Future Directions

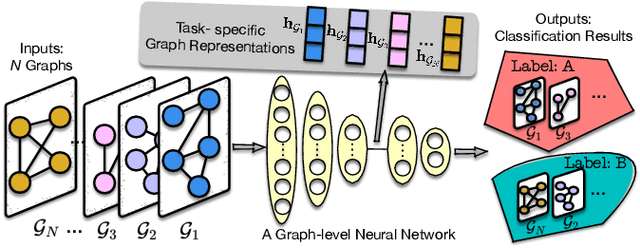
Graph-structured data consisting of objects (i.e., nodes) and relationships among objects (i.e., edges) are ubiquitous. Graph-level learning is a matter of studying a collection of graphs instead of a single graph. Traditional graph-level learning methods used to be the mainstream. However, with the increasing scale and complexity of graphs, Graph-level Neural Networks (GLNNs, deep learning-based graph-level learning methods) have been attractive due to their superiority in modeling high-dimensional data. Thus, a survey on GLNNs is necessary. To frame this survey, we propose a systematic taxonomy covering GLNNs upon deep neural networks, graph neural networks, and graph pooling. The representative and state-of-the-art models in each category are focused on this survey. We also investigate the reproducibility, benchmarks, and new graph datasets of GLNNs. Finally, we conclude future directions to further push forward GLNNs. The repository of this survey is available at https://github.com/GeZhangMQ/Awesome-Graph-level-Neural-Networks.

Projective Ranking-based GNN Evasion Attacks

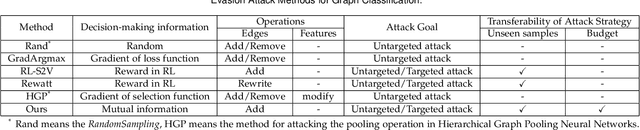
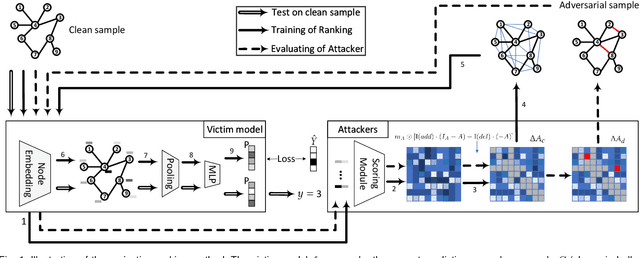
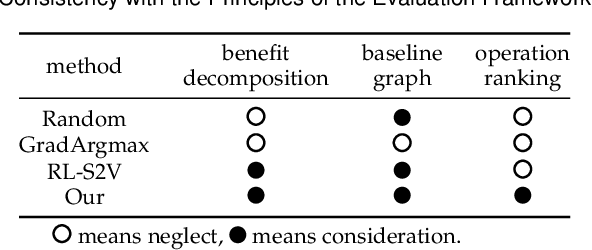
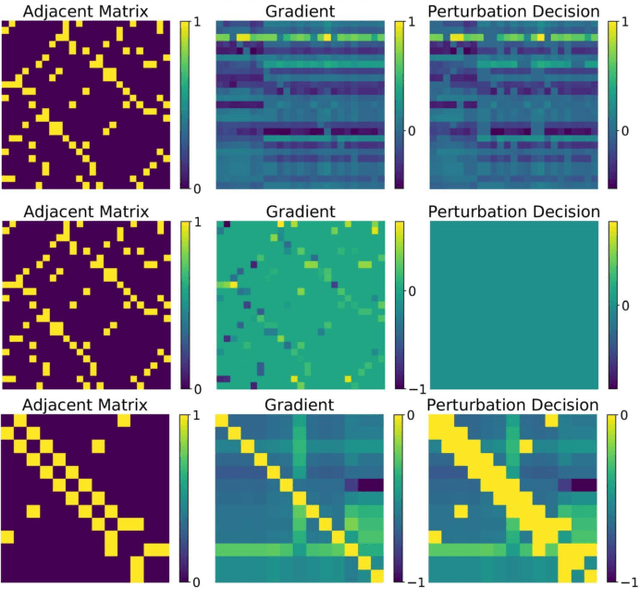
Graph neural networks (GNNs) offer promising learning methods for graph-related tasks. However, GNNs are at risk of adversarial attacks. Two primary limitations of the current evasion attack methods are highlighted: (1) The current GradArgmax ignores the "long-term" benefit of the perturbation. It is faced with zero-gradient and invalid benefit estimates in certain situations. (2) In the reinforcement learning-based attack methods, the learned attack strategies might not be transferable when the attack budget changes. To this end, we first formulate the perturbation space and propose an evaluation framework and the projective ranking method. We aim to learn a powerful attack strategy then adapt it as little as possible to generate adversarial samples under dynamic budget settings. In our method, based on mutual information, we rank and assess the attack benefits of each perturbation for an effective attack strategy. By projecting the strategy, our method dramatically minimizes the cost of learning a new attack strategy when the attack budget changes. In the comparative assessment with GradArgmax and RL-S2V, the results show our method owns high attack performance and effective transferability. The visualization of our method also reveals various attack patterns in the generation of adversarial samples.

Semi-Riemannian Graph Convolutional Networks

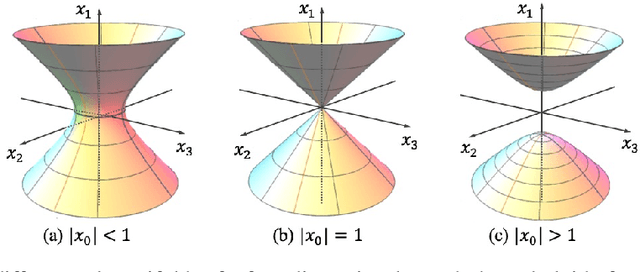
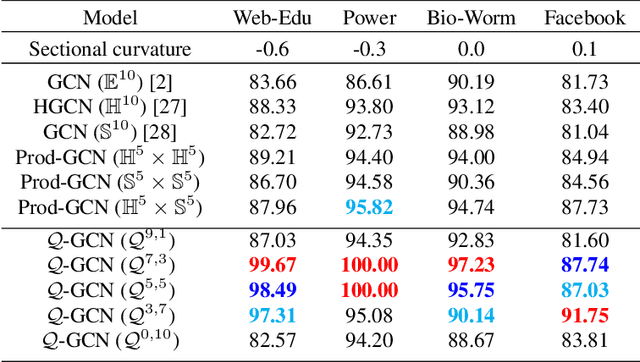
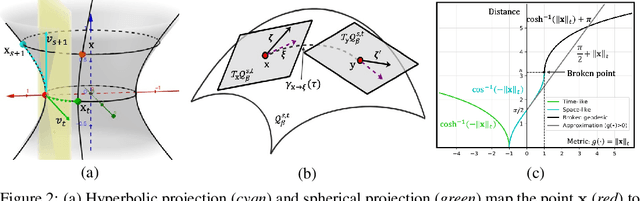
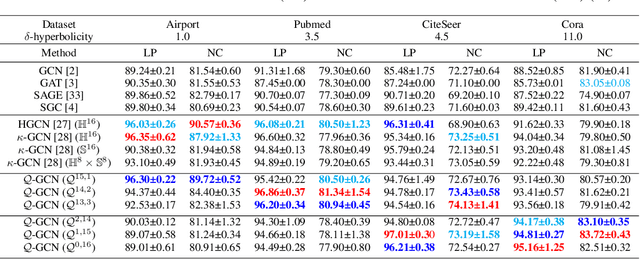
Graph Convolutional Networks (GCNs) are typically studied through the lens of Euclidean geometry. Non-Euclidean Riemannian manifolds provide specific inductive biases for embedding hierarchical or spherical data, but cannot align well with data of mixed topologies. We consider a larger class of semi-Riemannian manifolds with indefinite metric that generalize hyperboloid and sphere as well as their submanifolds. We develop new geodesic tools that allow for extending neural network operations into geodesically disconnected semi-Riemannian manifolds. As a consequence, we derive a principled Semi-Riemannian GCN that first models data in semi-Riemannian manifolds of constant nonzero curvature in the context of graph neural networks. Our method provides a geometric inductive bias that is sufficiently flexible to model mixed heterogeneous topologies like hierarchical graphs with cycles. Empirical results demonstrate that our method outperforms Riemannian counterparts when embedding graphs of complex topologies.

A Comprehensive Survey on Community Detection with Deep Learning

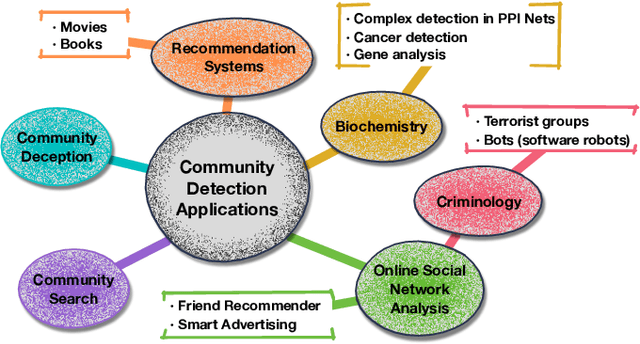
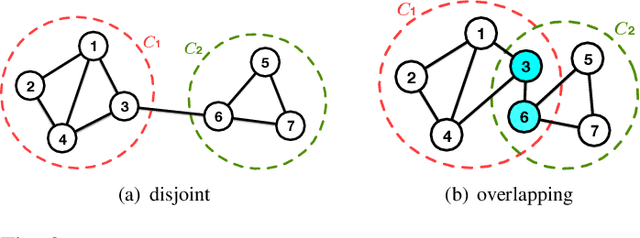
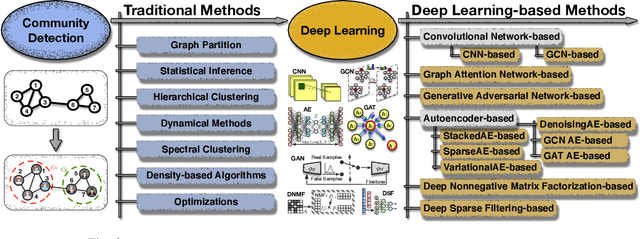
A community reveals the features and connections of its members that are different from those in other communities in a network. Detecting communities is of great significance in network analysis. Despite the classical spectral clustering and statistical inference methods, we notice a significant development of deep learning techniques for community detection in recent years with their advantages in handling high dimensional network data. Hence, a comprehensive overview of community detection's latest progress through deep learning is timely to both academics and practitioners. This survey devises and proposes a new taxonomy covering different categories of the state-of-the-art methods, including deep learning-based models upon deep neural networks, deep nonnegative matrix factorization and deep sparse filtering. The main category, i.e., deep neural networks, is further divided into convolutional networks, graph attention networks, generative adversarial networks and autoencoders. The survey also summarizes the popular benchmark data sets, model evaluation metrics, and open-source implementations to address experimentation settings. We then discuss the practical applications of community detection in various domains and point to implementation scenarios. Finally, we outline future directions by suggesting challenging topics in this fast-growing deep learning field.

Multi-Scale Contrastive Siamese Networks for Self-Supervised Graph Representation Learning

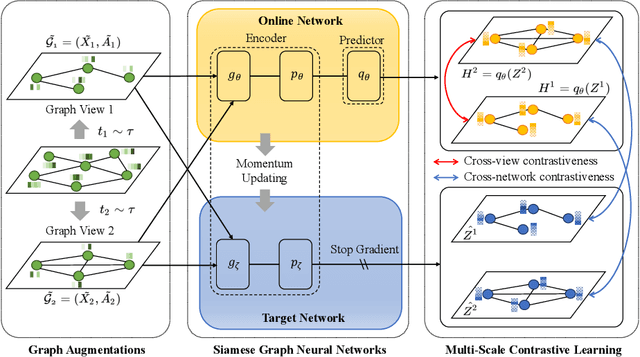
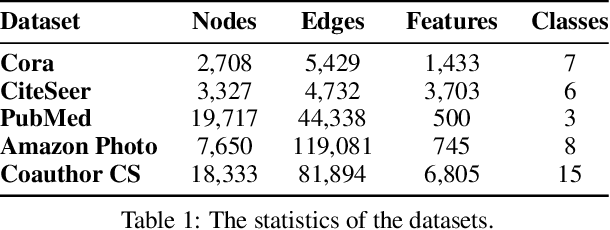
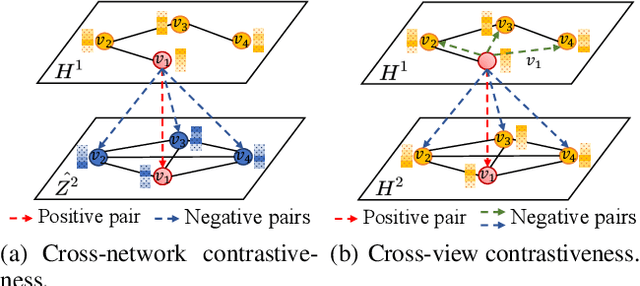
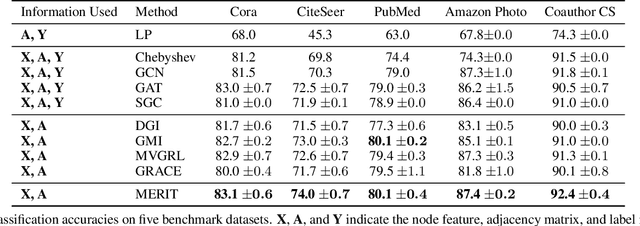
Graph representation learning plays a vital role in processing graph-structured data. However, prior arts on graph representation learning heavily rely on the labeling information. To overcome this problem, inspired by the recent success of graph contrastive learning and Siamese networks in visual representation learning, we propose a novel self-supervised approach in this paper to learn node representations by enhancing Siamese self-distillation with multi-scale contrastive learning. Specifically, we first generate two augmented views from the input graph based on local and global perspectives. Then, we employ two objectives called cross-view and cross-network contrastiveness to maximize the agreement between node representations across different views and networks. To demonstrate the effectiveness of our approach, we perform empirical experiments on five real-world datasets. Our method not only achieves new state-of-the-art results but also surpasses some semi-supervised counterparts by large margins.

Anomaly Detection on Attributed Networks via Contrastive Self-Supervised Learning

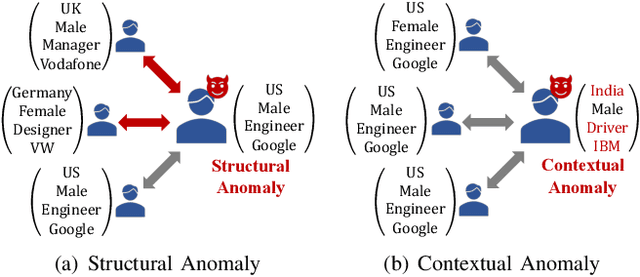
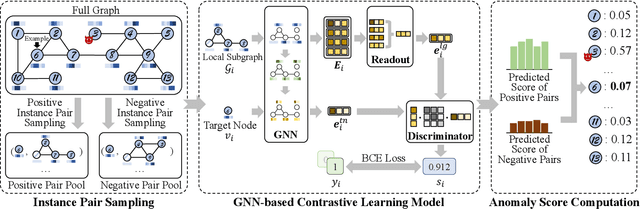
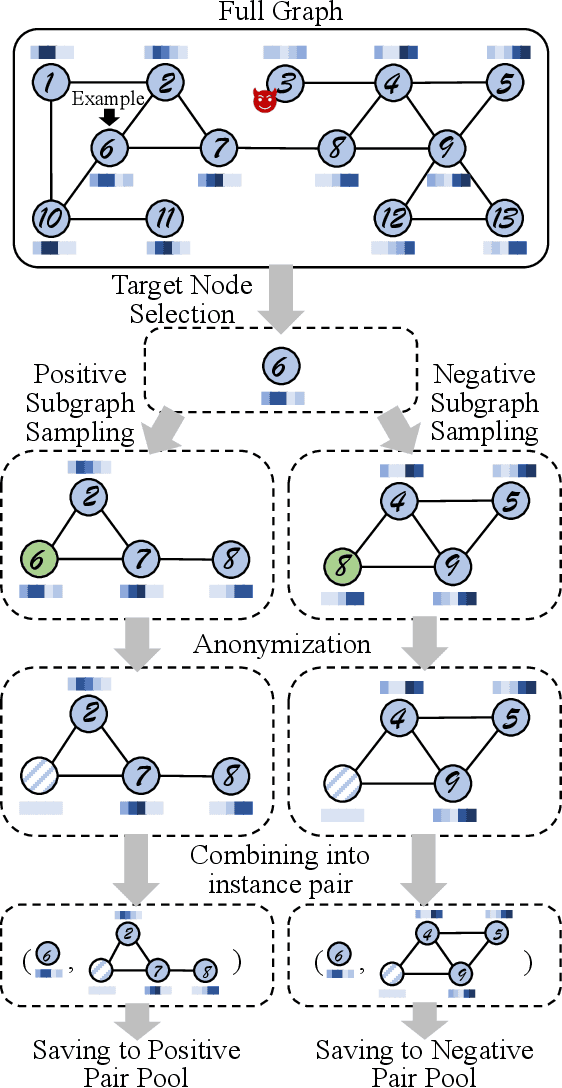
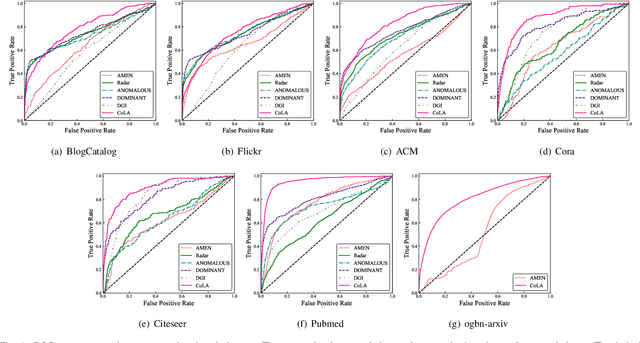
Anomaly detection on attributed networks attracts considerable research interests due to wide applications of attributed networks in modeling a wide range of complex systems. Recently, the deep learning-based anomaly detection methods have shown promising results over shallow approaches, especially on networks with high-dimensional attributes and complex structures. However, existing approaches, which employ graph autoencoder as their backbone, do not fully exploit the rich information of the network, resulting in suboptimal performance. Furthermore, these methods do not directly target anomaly detection in their learning objective and fail to scale to large networks due to the full graph training mechanism. To overcome these limitations, in this paper, we present a novel contrastive self-supervised learning framework for anomaly detection on attributed networks. Our framework fully exploits the local information from network data by sampling a novel type of contrastive instance pair, which can capture the relationship between each node and its neighboring substructure in an unsupervised way. Meanwhile, a well-designed graph neural network-based contrastive learning model is proposed to learn informative embedding from high-dimensional attributes and local structure and measure the agreement of each instance pairs with its outputted scores. The multi-round predicted scores by the contrastive learning model are further used to evaluate the abnormality of each node with statistical estimation. In this way, the learning model is trained by a specific anomaly detection-aware target. Furthermore, since the input of the graph neural network module is batches of instance pairs instead of the full network, our framework can adapt to large networks flexibly. Experimental results show that our proposed framework outperforms the state-of-the-art baseline methods on all seven benchmark datasets.