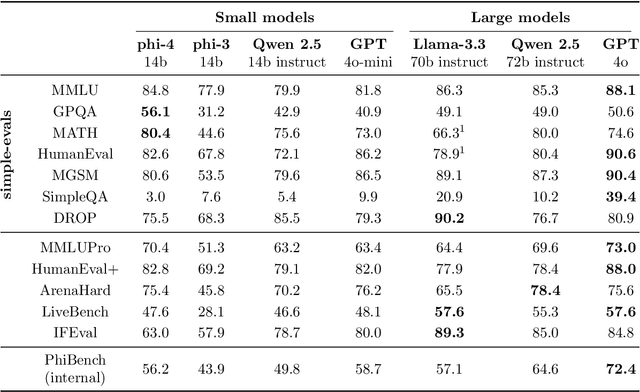
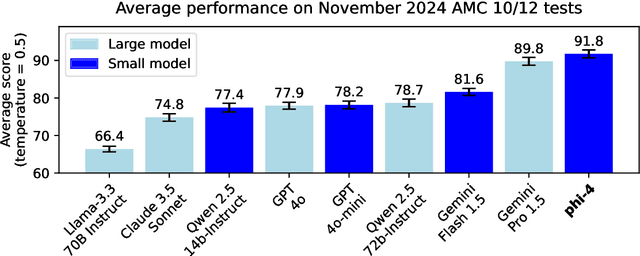
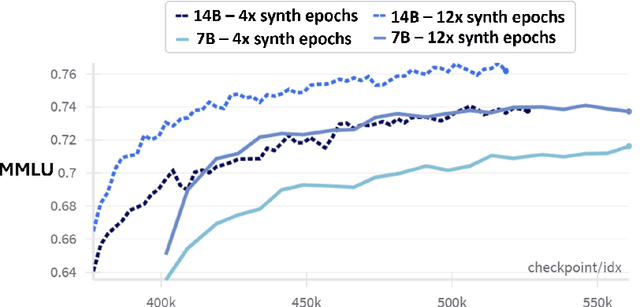
Phi-4 Technical Report

We present phi-4, a 14-billion parameter language model developed with a training recipe that is centrally focused on data quality. Unlike most language models, where pre-training is based primarily on organic data sources such as web content or code, phi-4 strategically incorporates synthetic data throughout the training process. While previous models in the Phi family largely distill the capabilities of a teacher model (specifically GPT-4), phi-4 substantially surpasses its teacher model on STEM-focused QA capabilities, giving evidence that our data-generation and post-training techniques go beyond distillation. Despite minimal changes to the phi-3 architecture, phi-4 achieves strong performance relative to its size -- especially on reasoning-focused benchmarks -- due to improved data, training curriculum, and innovations in the post-training scheme.

Long-time asymptotics of noisy SVGD outside the population limit

Stein Variational Gradient Descent (SVGD) is a widely used sampling algorithm that has been successfully applied in several areas of Machine Learning. SVGD operates by iteratively moving a set of interacting particles (which represent the samples) to approximate the target distribution. Despite recent studies on the complexity of SVGD and its variants, their long-time asymptotic behavior (i.e., after numerous iterations ) is still not understood in the finite number of particles regime. We study the long-time asymptotic behavior of a noisy variant of SVGD. First, we establish that the limit set of noisy SVGD for large is well-defined. We then characterize this limit set, showing that it approaches the target distribution as increases. In particular, noisy SVGD provably avoids the variance collapse observed for SVGD. Our approach involves demonstrating that the trajectories of noisy SVGD closely resemble those described by a McKean-Vlasov process.

Phi-3 Technical Report: A Highly Capable Language Model Locally on Your Phone

We introduce phi-3-mini, a 3.8 billion parameter language model trained on 3.3 trillion tokens, whose overall performance, as measured by both academic benchmarks and internal testing, rivals that of models such as Mixtral 8x7B and GPT-3.5 (e.g., phi-3-mini achieves 69% on MMLU and 8.38 on MT-bench), despite being small enough to be deployed on a phone. The innovation lies entirely in our dataset for training, a scaled-up version of the one used for phi-2, composed of heavily filtered web data and synthetic data. The model is also further aligned for robustness, safety, and chat format. We also provide some initial parameter-scaling results with a 7B and 14B models trained for 4.8T tokens, called phi-3-small and phi-3-medium, both significantly more capable than phi-3-mini (e.g., respectively 75% and 78% on MMLU, and 8.7 and 8.9 on MT-bench).

Gaussian random field approximation via Stein's method with applications to wide random neural networks

We derive upper bounds on the Wasserstein distance ($W_1$), with respect to $\sup$-norm, between any continuous $\mathbb{R}^d$ valued random field indexed by the $n$-sphere and the Gaussian, based on Stein's method. We develop a novel Gaussian smoothing technique that allows us to transfer a bound in a smoother metric to the $W_1$ distance. The smoothing is based on covariance functions constructed using powers of Laplacian operators, designed so that the associated Gaussian process has a tractable Cameron-Martin or Reproducing Kernel Hilbert Space. This feature enables us to move beyond one dimensional interval-based index sets that were previously considered in the literature. Specializing our general result, we obtain the first bounds on the Gaussian random field approximation of wide random neural networks of any depth and Lipschitz activation functions at the random field level. Our bounds are explicitly expressed in terms of the widths of the network and moments of the random weights. We also obtain tighter bounds when the activation function has three bounded derivatives.

Textbooks Are All You Need

We introduce phi-1, a new large language model for code, with significantly smaller size than competing models: phi-1 is a Transformer-based model with 1.3B parameters, trained for 4 days on 8 A100s, using a selection of ``textbook quality" data from the web (6B tokens) and synthetically generated textbooks and exercises with GPT-3.5 (1B tokens). Despite this small scale, phi-1 attains pass@1 accuracy 50.6% on HumanEval and 55.5% on MBPP. It also displays surprising emergent properties compared to phi-1-base, our model before our finetuning stage on a dataset of coding exercises, and phi-1-small, a smaller model with 350M parameters trained with the same pipeline as phi-1 that still achieves 45% on HumanEval.

The probability flow ODE is provably fast

We provide the first polynomial-time convergence guarantees for the probability flow ODE implementation (together with a corrector step) of score-based generative modeling. Our analysis is carried out in the wake of recent results obtaining such guarantees for the SDE-based implementation (i.e., denoising diffusion probabilistic modeling or DDPM), but requires the development of novel techniques for studying deterministic dynamics without contractivity. Through the use of a specially chosen corrector step based on the underdamped Langevin diffusion, we obtain better dimension dependence than prior works on DDPM ($O(\sqrt{d})$ vs. $O(d)$, assuming smoothness of the data distribution), highlighting potential advantages of the ODE framework.

Forward-backward Gaussian variational inference via JKO in the Bures-Wasserstein Space

Variational inference (VI) seeks to approximate a target distribution $\pi$ by an element of a tractable family of distributions. Of key interest in statistics and machine learning is Gaussian VI, which approximates $\pi$ by minimizing the Kullback-Leibler (KL) divergence to $\pi$ over the space of Gaussians. In this work, we develop the (Stochastic) Forward-Backward Gaussian Variational Inference (FB-GVI) algorithm to solve Gaussian VI. Our approach exploits the composite structure of the KL divergence, which can be written as the sum of a smooth term (the potential) and a non-smooth term (the entropy) over the Bures-Wasserstein (BW) space of Gaussians endowed with the Wasserstein distance. For our proposed algorithm, we obtain state-of-the-art convergence guarantees when $\pi$ is log-smooth and log-concave, as well as the first convergence guarantees to first-order stationary solutions when $\pi$ is only log-smooth.

Sampling is as easy as learning the score: theory for diffusion models with minimal data assumptions

We provide theoretical convergence guarantees for score-based generative models (SGMs) such as denoising diffusion probabilistic models (DDPMs), which constitute the backbone of large-scale real-world generative models such as DALL$\cdot$E 2. Our main result is that, assuming accurate score estimates, such SGMs can efficiently sample from essentially any realistic data distribution. In contrast to prior works, our results (1) hold for an $L^2$-accurate score estimate (rather than $L^\infty$-accurate); (2) do not require restrictive functional inequality conditions that preclude substantial non-log-concavity; (3) scale polynomially in all relevant problem parameters; and (4) match state-of-the-art complexity guarantees for discretization of the Langevin diffusion, provided that the score error is sufficiently small. We view this as strong theoretical justification for the empirical success of SGMs. We also examine SGMs based on the critically damped Langevin diffusion (CLD). Contrary to conventional wisdom, we provide evidence that the use of the CLD does not reduce the complexity of SGMs.

Federated Learning with a Sampling Algorithm under Isoperimetry

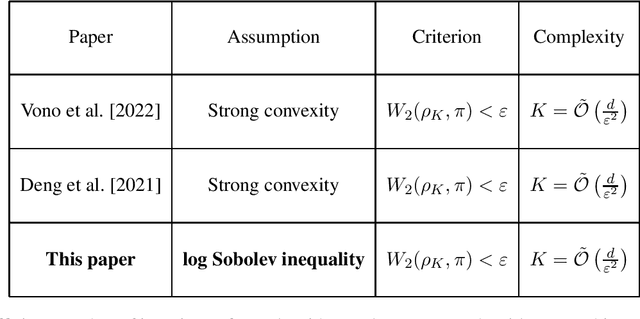
Federated learning uses a set of techniques to efficiently distribute the training of a machine learning algorithm across several devices, who own the training data. These techniques critically rely on reducing the communication cost -- the main bottleneck -- between the devices and a central server. Federated learning algorithms usually take an optimization approach: they are algorithms for minimizing the training loss subject to communication (and other) constraints. In this work, we instead take a Bayesian approach for the training task, and propose a communication-efficient variant of the Langevin algorithm to sample a posteriori. The latter approach is more robust and provides more knowledge of the \textit{a posteriori} distribution than its optimization counterpart. We analyze our algorithm without assuming that the target distribution is strongly log-concave. Instead, we assume the weaker log Sobolev inequality, which allows for nonconvexity.

Improved analysis for a proximal algorithm for sampling

We study the proximal sampler of Lee, Shen, and Tian (2021) and obtain new convergence guarantees under weaker assumptions than strong log-concavity: namely, our results hold for (1) weakly log-concave targets, and (2) targets satisfying isoperimetric assumptions which allow for non-log-concavity. We demonstrate our results by obtaining new state-of-the-art sampling guarantees for several classes of target distributions. We also strengthen the connection between the proximal sampler and the proximal method in optimization by interpreting the proximal sampler as an entropically regularized Wasserstein proximal method, and the proximal point method as the limit of the proximal sampler with vanishing noise.