Integrated Analysis for Electronic Health Records with Structured and Sporadic Missingness

Objectives: We propose a novel imputation method tailored for Electronic Health Records (EHRs) with structured and sporadic missingness. Such missingness frequently arises in the integration of heterogeneous EHR datasets for downstream clinical applications. By addressing these gaps, our method provides a practical solution for integrated analysis, enhancing data utility and advancing the understanding of population health. Materials and Methods: We begin by demonstrating structured and sporadic missing mechanisms in the integrated analysis of EHR data. Following this, we introduce a novel imputation framework, Macomss, specifically designed to handle structurally and heterogeneously occurring missing data. We establish theoretical guarantees for Macomss, ensuring its robustness in preserving the integrity and reliability of integrated analyses. To assess its empirical performance, we conduct extensive simulation studies that replicate the complex missingness patterns observed in real-world EHR systems, complemented by validation using EHR datasets from the Duke University Health System (DUHS). Results: Simulation studies show that our approach consistently outperforms existing imputation methods. Using datasets from three hospitals within DUHS, Macomss achieves the lowest imputation errors for missing data in most cases and provides superior or comparable downstream prediction performance compared to benchmark methods. Conclusions: We provide a theoretically guaranteed and practically meaningful method for imputing structured and sporadic missing data, enabling accurate and reliable integrated analysis across multiple EHR datasets. The proposed approach holds significant potential for advancing research in population health.

Revisit CP Tensor Decomposition: Statistical Optimality and Fast Convergence

Canonical Polyadic (CP) tensor decomposition is a fundamental technique for analyzing high-dimensional tensor data. While the Alternating Least Squares (ALS) algorithm is widely used for computing CP decomposition due to its simplicity and empirical success, its theoretical foundation, particularly regarding statistical optimality and convergence behavior, remain underdeveloped, especially in noisy, non-orthogonal, and higher-rank settings. In this work, we revisit CP tensor decomposition from a statistical perspective and provide a comprehensive theoretical analysis of ALS under a signal-plus-noise model. We establish non-asymptotic, minimax-optimal error bounds for tensors of general order, dimensions, and rank, assuming suitable initialization. To enable such initialization, we propose Tucker-based Approximation with Simultaneous Diagonalization (TASD), a robust method that improves stability and accuracy in noisy regimes. Combined with ALS, TASD yields a statistically consistent estimator. We further analyze the convergence dynamics of ALS, identifying a two-phase pattern-initial quadratic convergence followed by linear refinement. We further show that in the rank-one setting, ALS with an appropriately chosen initialization attains optimal error within just one or two iterations.

Federated PCA and Estimation for Spiked Covariance Matrices: Optimal Rates and Efficient Algorithm

Federated Learning (FL) has gained significant recent attention in machine learning for its enhanced privacy and data security, making it indispensable in fields such as healthcare, finance, and personalized services. This paper investigates federated PCA and estimation for spiked covariance matrices under distributed differential privacy constraints. We establish minimax rates of convergence, with a key finding that the central server's optimal rate is the harmonic mean of the local clients' minimax rates. This guarantees consistent estimation at the central server as long as at least one local client provides consistent results. Notably, consistency is maintained even if some local estimators are inconsistent, provided there are enough clients. These findings highlight the robustness and scalability of FL for reliable statistical inference under privacy constraints. To establish minimax lower bounds, we derive a matrix version of van Trees' inequality, which is of independent interest. Furthermore, we propose an efficient algorithm that preserves differential privacy while achieving near-optimal rates at the central server, up to a logarithmic factor. We address significant technical challenges in analyzing this algorithm, which involves a three-layer spectral decomposition. Numerical performance of the proposed algorithm is investigated using both simulated and real data.

Tensor Decomposition with Unaligned Observations

This paper presents a canonical polyadic (CP) tensor decomposition that addresses unaligned observations. The mode with unaligned observations is represented using functions in a reproducing kernel Hilbert space (RKHS). We introduce a versatile loss function that effectively accounts for various types of data, including binary, integer-valued, and positive-valued types. Additionally, we propose an optimization algorithm for computing tensor decompositions with unaligned observations, along with a stochastic gradient method to enhance computational efficiency. A sketching algorithm is also introduced to further improve efficiency when using the $\ell_2$ loss function. To demonstrate the efficacy of our methods, we provide illustrative examples using both synthetic data and an early childhood human microbiome dataset.

Tensor Decomposition Meets RKHS: Efficient Algorithms for Smooth and Misaligned Data

The canonical polyadic (CP) tensor decomposition decomposes a multidimensional data array into a sum of outer products of finite-dimensional vectors. Instead, we can replace some or all of the vectors with continuous functions (infinite-dimensional vectors) from a reproducing kernel Hilbert space (RKHS). We refer to tensors with some infinite-dimensional modes as quasitensors, and the approach of decomposing a tensor with some continuous RKHS modes is referred to as CP-HiFi (hybrid infinite and finite dimensional) tensor decomposition. An advantage of CP-HiFi is that it can enforce smoothness in the infinite dimensional modes. Further, CP-HiFi does not require the observed data to lie on a regular and finite rectangular grid and naturally incorporates misaligned data. We detail the methodology and illustrate it on a synthetic example.

Fast and Reliable Generation of EHR Time Series via Diffusion Models

Electronic Health Records (EHRs) are rich sources of patient-level data, including laboratory tests, medications, and diagnoses, offering valuable resources for medical data analysis. However, concerns about privacy often restrict access to EHRs, hindering downstream analysis. Researchers have explored various methods for generating privacy-preserving EHR data. In this study, we introduce a new method for generating diverse and realistic synthetic EHR time series data using Denoising Diffusion Probabilistic Models (DDPM). We conducted experiments on six datasets, comparing our proposed method with seven existing methods. Our results demonstrate that our approach significantly outperforms all existing methods in terms of data utility while requiring less training effort. Our approach also enhances downstream medical data analysis by providing diverse and realistic synthetic EHR data.

Mode-wise Principal Subspace Pursuit and Matrix Spiked Covariance Model

This paper introduces a novel framework called Mode-wise Principal Subspace Pursuit (MOP-UP) to extract hidden variations in both the row and column dimensions for matrix data. To enhance the understanding of the framework, we introduce a class of matrix-variate spiked covariance models that serve as inspiration for the development of the MOP-UP algorithm. The MOP-UP algorithm consists of two steps: Average Subspace Capture (ASC) and Alternating Projection (AP). These steps are specifically designed to capture the row-wise and column-wise dimension-reduced subspaces which contain the most informative features of the data. ASC utilizes a novel average projection operator as initialization and achieves exact recovery in the noiseless setting. We analyze the convergence and non-asymptotic error bounds of MOP-UP, introducing a blockwise matrix eigenvalue perturbation bound that proves the desired bound, where classic perturbation bounds fail. The effectiveness and practical merits of the proposed framework are demonstrated through experiments on both simulated and real datasets. Lastly, we discuss generalizations of our approach to higher-order data.

Phase transition for detecting a small community in a large network

How to detect a small community in a large network is an interesting problem, including clique detection as a special case, where a naive degree-based $\chi^2$-test was shown to be powerful in the presence of an Erd\H{o}s-Renyi background. Using Sinkhorn's theorem, we show that the signal captured by the $\chi^2$-test may be a modeling artifact, and it may disappear once we replace the Erd\H{o}s-Renyi model by a broader network model. We show that the recent SgnQ test is more appropriate for such a setting. The test is optimal in detecting communities with sizes comparable to the whole network, but has never been studied for our setting, which is substantially different and more challenging. Using a degree-corrected block model (DCBM), we establish phase transitions of this testing problem concerning the size of the small community and the edge densities in small and large communities. When the size of the small community is larger than $\sqrt{n}$, the SgnQ test is optimal for it attains the computational lower bound (CLB), the information lower bound for methods allowing polynomial computation time. When the size of the small community is smaller than $\sqrt{n}$, we establish the parameter regime where the SgnQ test has full power and make some conjectures of the CLB. We also study the classical information lower bound (LB) and show that there is always a gap between the CLB and LB in our range of interest.

Sampling is as easy as learning the score: theory for diffusion models with minimal data assumptions

We provide theoretical convergence guarantees for score-based generative models (SGMs) such as denoising diffusion probabilistic models (DDPMs), which constitute the backbone of large-scale real-world generative models such as DALL$\cdot$E 2. Our main result is that, assuming accurate score estimates, such SGMs can efficiently sample from essentially any realistic data distribution. In contrast to prior works, our results (1) hold for an $L^2$-accurate score estimate (rather than $L^\infty$-accurate); (2) do not require restrictive functional inequality conditions that preclude substantial non-log-concavity; (3) scale polynomially in all relevant problem parameters; and (4) match state-of-the-art complexity guarantees for discretization of the Langevin diffusion, provided that the score error is sufficiently small. We view this as strong theoretical justification for the empirical success of SGMs. We also examine SGMs based on the critically damped Langevin diffusion (CLD). Contrary to conventional wisdom, we provide evidence that the use of the CLD does not reduce the complexity of SGMs.

Self-supervised Denoising via Low-rank Tensor Approximated Convolutional Neural Network

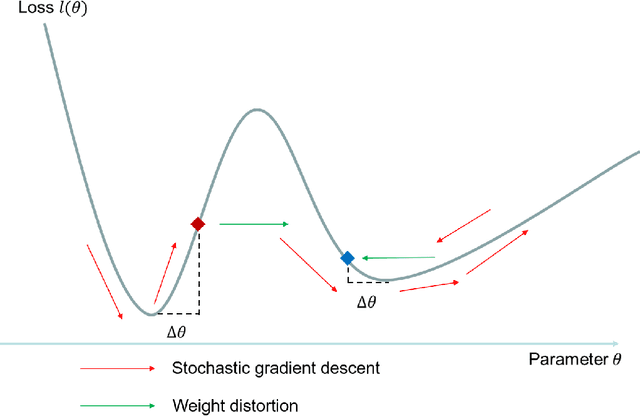
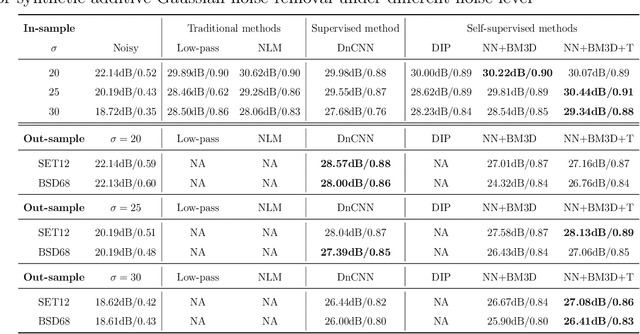
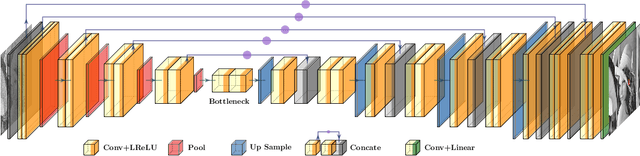
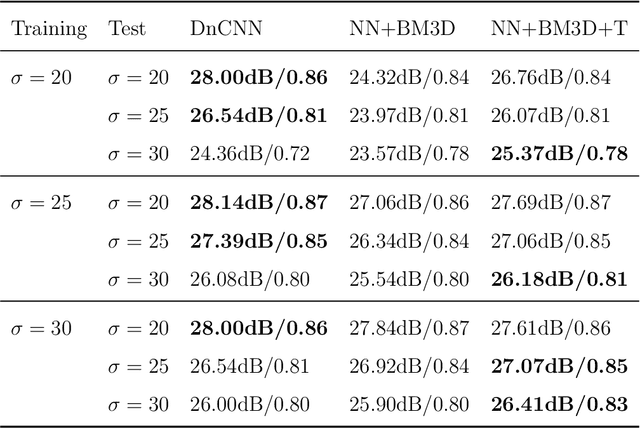
Noise is ubiquitous during image acquisition. Sufficient denoising is often an important first step for image processing. In recent decades, deep neural networks (DNNs) have been widely used for image denoising. Most DNN-based image denoising methods require a large-scale dataset or focus on supervised settings, in which single/pairs of clean images or a set of noisy images are required. This poses a significant burden on the image acquisition process. Moreover, denoisers trained on datasets of limited scale may incur over-fitting. To mitigate these issues, we introduce a new self-supervised framework for image denoising based on the Tucker low-rank tensor approximation. With the proposed design, we are able to characterize our denoiser with fewer parameters and train it based on a single image, which considerably improves the model generalizability and reduces the cost of data acquisition. Extensive experiments on both synthetic and real-world noisy images have been conducted. Empirical results show that our proposed method outperforms existing non-learning-based methods (e.g., low-pass filter, non-local mean), single-image unsupervised denoisers (e.g., DIP, NN+BM3D) evaluated on both in-sample and out-sample datasets. The proposed method even achieves comparable performances with some supervised methods (e.g., DnCNN).