Long-time asymptotics of noisy SVGD outside the population limit

Stein Variational Gradient Descent (SVGD) is a widely used sampling algorithm that has been successfully applied in several areas of Machine Learning. SVGD operates by iteratively moving a set of interacting particles (which represent the samples) to approximate the target distribution. Despite recent studies on the complexity of SVGD and its variants, their long-time asymptotic behavior (i.e., after numerous iterations ) is still not understood in the finite number of particles regime. We study the long-time asymptotic behavior of a noisy variant of SVGD. First, we establish that the limit set of noisy SVGD for large is well-defined. We then characterize this limit set, showing that it approaches the target distribution as increases. In particular, noisy SVGD provably avoids the variance collapse observed for SVGD. Our approach involves demonstrating that the trajectories of noisy SVGD closely resemble those described by a McKean-Vlasov process.

Stochastic Subgradient Descent Escapes Active Strict Saddles

In non-smooth stochastic optimization, we establish the non-convergence of the stochastic subgradient descent (SGD) to the critical points recently called active strict saddles by Davis and Drusvyatskiy. Such points lie on a manifold $M$ where the function $f$ has a direction of second-order negative curvature. Off this manifold, the norm of the Clarke subdifferential of $f$ is lower-bounded. We require two conditions on $f$. The first assumption is a Verdier stratification condition, which is a refinement of the popular Whitney stratification. It allows us to establish a reinforced version of the projection formula of Bolte \emph{et.al.} for Whitney stratifiable functions, and which is of independent interest. The second assumption, termed the angle condition, allows to control the distance of the iterates to $M$. When $f$ is weakly convex, our assumptions are generic. Consequently, generically in the class of definable weakly convex functions, the SGD converges to a local minimizer.

Analysis of a Target-Based Actor-Critic Algorithm with Linear Function Approximation

Actor-critic methods integrating target networks have exhibited a stupendous empirical success in deep reinforcement learning. However, a theoretical understanding of the use of target networks in actor-critic methods is largely missing in the literature. In this paper, we bridge this gap between theory and practice by proposing the first theoretical analysis of an online target-based actor-critic algorithm with linear function approximation in the discounted reward setting. Our algorithm uses three different timescales: one for the actor and two for the critic. Instead of using the standard single timescale temporal difference (TD) learning algorithm as a critic, we use a two timescales target-based version of TD learning closely inspired from practical actor-critic algorithms implementing target networks. First, we establish asymptotic convergence results for both the critic and the actor under Markovian sampling. Then, we provide a finite-time analysis showing the impact of incorporating a target network into actor-critic methods.

Conditional independence testing via weighted partial copulas

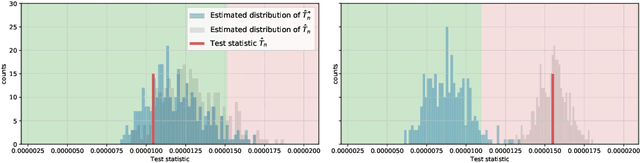
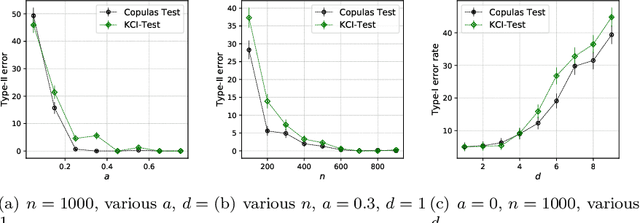
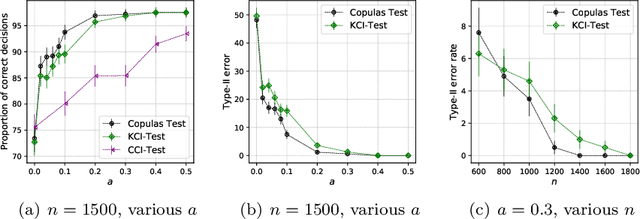
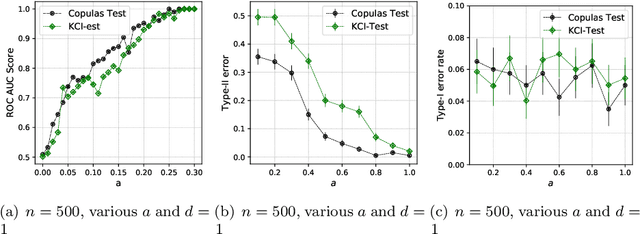
This paper introduces the \textit{weighted partial copula} function for testing conditional independence. The proposed test procedure results from these two ingredients: (i) the test statistic is an explicit Cramer-von Mises transformation of the \textit{weighted partial copula}, (ii) the regions of rejection are computed using a bootstrap procedure which mimics conditional independence by generating samples from the product measure of the estimated conditional marginals. Under conditional independence, the weak convergence of the \textit{weighted partial copula proces}s is established when the marginals are estimated using a smoothed local linear estimator. Finally, an experimental section demonstrates that the proposed test has competitive power compared to recent state-of-the-art methods such as kernel-based test.

Convergence Analysis of a Momentum Algorithm with Adaptive Step Size for Non Convex Optimization

Although ADAM is a very popular algorithm for optimizing the weights of neural networks, it has been recently shown that it can diverge even in simple convex optimization examples. Several variants of ADAM have been proposed to circumvent this convergence issue. In this work, we study the ADAM algorithm for smooth nonconvex optimization under a boundedness assumption on the adaptive learning rate. The bound on the adaptive step size depends on the Lipschitz constant of the gradient of the objective function and provides safe theoretical adaptive step sizes. Under this boundedness assumption, we show a novel first order convergence rate result in both deterministic and stochastic contexts. Furthermore, we establish convergence rates of the function value sequence using the Kurdyka-Lojasiewicz property.

A Fully Stochastic Primal-Dual Algorithm

A new stochastic primal-dual algorithm for solving a composite optimization problem is proposed. It is assumed that all the functions/matrix used to define the optimization problem are given as statistical expectations. These expectations are unknown but revealed across time through i.i.d realizations. This covers the case of convex optimization under stochastic linear constraints. The proposed algorithm is proven to converge to a saddle point of the Lagrangian function. In the framework of the monotone operator theory, the convergence proof relies on recent results on the stochastic Forward Backward algorithm involving random monotone operators.

A Constant Step Stochastic Douglas-Rachford Algorithm with Application to Non Separable Regularizations

The Douglas Rachford algorithm is an algorithm that converges to a minimizer of a sum of two convex functions. The algorithm consists in fixed point iterations involving computations of the proximity operators of the two functions separately. The paper investigates a stochastic version of the algorithm where both functions are random and the step size is constant. We establish that the iterates of the algorithm stay close to the set of solution with high probability when the step size is small enough. Application to structured regularization is considered.

Snake: a Stochastic Proximal Gradient Algorithm for Regularized Problems over Large Graphs

A regularized optimization problem over a large unstructured graph is studied, where the regularization term is tied to the graph geometry. Typical regularization examples include the total variation and the Laplacian regularizations over the graph. When applying the proximal gradient algorithm to solve this problem, there exist quite affordable methods to implement the proximity operator (backward step) in the special case where the graph is a simple path without loops. In this paper, an algorithm, referred to as "Snake", is proposed to solve such regularized problems over general graphs, by taking benefit of these fast methods. The algorithm consists in properly selecting random simple paths in the graph and performing the proximal gradient algorithm over these simple paths. This algorithm is an instance of a new general stochastic proximal gradient algorithm, whose convergence is proven. Applications to trend filtering and graph inpainting are provided among others. Numerical experiments are conducted over large graphs.