Mitigating Position-Shift Failures in Text-Based Modular Arithmetic via Position Curriculum and Template Diversity

Building on insights from the grokking literature, we study character-level Transformers trained to compute modular addition from text, and focus on robustness under input-format variation rather than only in-distribution accuracy. We identify a previously under-emphasized failure mode: models that achieve high in-distribution accuracy can fail catastrophically when the same expression is shifted to different absolute character positions ("position shift") or presented under out-of-distribution natural-language templates. Using a disjoint-pair split over all ordered pairs for p=97, we show that a baseline model reaches strong in-distribution performance yet collapses under position shift and template OOD. We then introduce a simple training recipe that combines (i) explicit expression boundary markers, (ii) position curriculum that broadens the range of absolute positions seen during training, (iii) diverse template mixtures, and (iv) consistency training across multiple variants per example. Across three seeds, this intervention substantially improves robustness to position shift and template OOD while maintaining high in-distribution accuracy, whereas an ALiBi-style ablation fails to learn the task under our setup. Our results suggest that steering procedural generalization under noisy supervision benefits from explicitly training invariances that are otherwise absent from the data distribution, and we provide a reproducible evaluation protocol and artifacts.

Group Representational Position Encoding

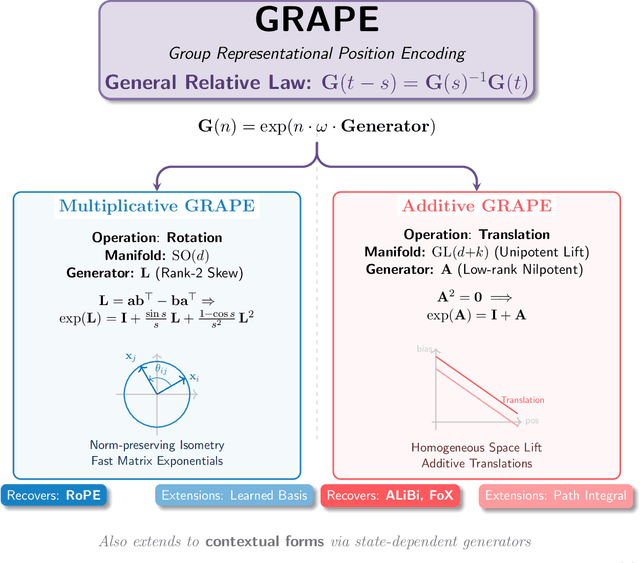
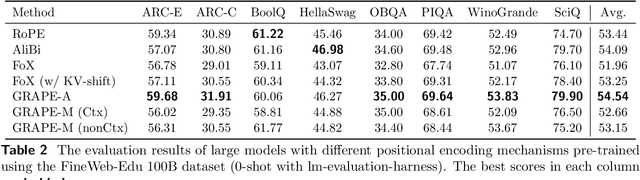
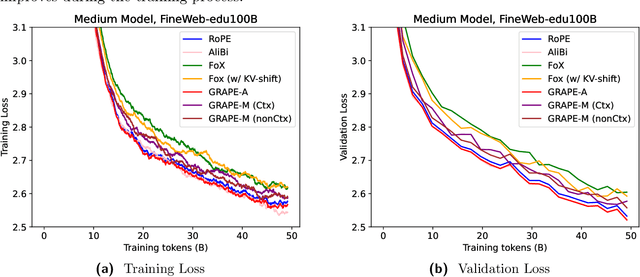
We present GRAPE (Group RepresentAtional Position Encoding), a unified framework for positional encoding based on group actions. GRAPE brings together two families of mechanisms: (i) multiplicative rotations (Multiplicative GRAPE) in $\mathrm{SO}(d)$ and (ii) additive logit biases (Additive GRAPE) arising from unipotent actions in the general linear group $\mathrm{GL}$. In Multiplicative GRAPE, a position $n \in \mathbb{Z}$ (or $t \in \mathbb{R}$) acts as $\mathbf{G}(n)=\exp(n\,ω\,\mathbf{L})$ with a rank-2 skew generator $\mathbf{L} \in \mathbb{R}^{d \times d}$, yielding a relative, compositional, norm-preserving map with a closed-form matrix exponential. RoPE is recovered exactly when the $d/2$ planes are the canonical coordinate pairs with log-uniform spectrum. Learned commuting subspaces and compact non-commuting mixtures strictly extend this geometry to capture cross-subspace feature coupling at $O(d)$ and $O(r d)$ cost per head, respectively. In Additive GRAPE, additive logits arise as rank-1 (or low-rank) unipotent actions, recovering ALiBi and the Forgetting Transformer (FoX) as exact special cases while preserving an exact relative law and streaming cacheability. Altogether, GRAPE supplies a principled design space for positional geometry in long-context models, subsuming RoPE and ALiBi as special cases. Project Page: https://github.com/model-architectures/GRAPE.

HoPE: Hyperbolic Rotary Positional Encoding for Stable Long-Range Dependency Modeling in Large Language Models

Positional encoding mechanisms enable Transformers to model sequential structure and long-range dependencies in text. While absolute positional encodings struggle with extrapolation to longer sequences due to fixed positional representations, and relative approaches like Alibi exhibit performance degradation on extremely long contexts, the widely-used Rotary Positional Encoding (RoPE) introduces oscillatory attention patterns that hinder stable long-distance dependency modelling. We address these limitations through a geometric reformulation of positional encoding. Drawing inspiration from Lorentz transformations in hyperbolic geometry, we propose Hyperbolic Rotary Positional Encoding (HoPE), which leverages hyperbolic functions to implement Lorentz rotations on token representations. Theoretical analysis demonstrates that RoPE is a special case of our generalized formulation. HoPE fundamentally resolves RoPE's slation issues by enforcing monotonic decay of attention weights with increasing token distances. Extensive experimental results, including perplexity evaluations under several extended sequence benchmarks, show that HoPE consistently exceeds existing positional encoding methods. These findings underscore HoPE's enhanced capacity for representing and generalizing long-range dependencies. Data and code will be available.

A standard transformer and attention with linear biases for molecular conformer generation

Sampling low-energy molecular conformations, spatial arrangements of atoms in a molecule, is a critical task for many different calculations performed in the drug discovery and optimization process. Numerous specialized equivariant networks have been designed to generate molecular conformations from 2D molecular graphs. Recently, non-equivariant transformer models have emerged as a viable alternative due to their capability to scale to improve generalization. However, the concern has been that non-equivariant models require a large model size to compensate the lack of equivariant bias. In this paper, we demonstrate that a well-chosen positional encoding effectively addresses these size limitations. A standard transformer model incorporating relative positional encoding for molecular graphs when scaled to 25 million parameters surpasses the current state-of-the-art non-equivariant base model with 64 million parameters on the GEOM-DRUGS benchmark. We implemented relative positional encoding as a negative attention bias that linearly increases with the shortest path distances between graph nodes at varying slopes for different attention heads, similar to ALiBi, a widely adopted relative positional encoding technique in the NLP domain. This architecture has the potential to serve as a foundation for a novel class of generative models for molecular conformations.

SeqPE: Transformer with Sequential Position Encoding

Since self-attention layers in Transformers are permutation invariant by design, positional encodings must be explicitly incorporated to enable spatial understanding. However, fixed-size lookup tables used in traditional learnable position embeddings (PEs) limit extrapolation capabilities beyond pre-trained sequence lengths. Expert-designed methods such as ALiBi and RoPE, mitigate this limitation but demand extensive modifications for adapting to new modalities, underscoring fundamental challenges in adaptability and scalability. In this work, we present SeqPE, a unified and fully learnable position encoding framework that represents each $n$-dimensional position index as a symbolic sequence and employs a lightweight sequential position encoder to learn their embeddings in an end-to-end manner. To regularize SeqPE's embedding space, we introduce two complementary objectives: a contrastive objective that aligns embedding distances with a predefined position-distance function, and a knowledge distillation loss that anchors out-of-distribution position embeddings to in-distribution teacher representations, further enhancing extrapolation performance. Experiments across language modeling, long-context question answering, and 2D image classification demonstrate that SeqPE not only surpasses strong baselines in perplexity, exact match (EM), and accuracy--particularly under context length extrapolation--but also enables seamless generalization to multi-dimensional inputs without requiring manual architectural redesign. We release our code, data, and checkpoints at https://github.com/ghrua/seqpe.

Theoretical Analysis of Positional Encodings in Transformer Models: Impact on Expressiveness and Generalization

Positional encodings are a core part of transformer-based models, enabling processing of sequential data without recurrence. This paper presents a theoretical framework to analyze how various positional encoding methods, including sinusoidal, learned, relative, and bias-based methods like Attention with Linear Biases (ALiBi), impact a transformer's expressiveness, generalization ability, and extrapolation to longer sequences. Expressiveness is defined via function approximation, generalization bounds are established using Rademacher complexity, and new encoding methods based on orthogonal functions, such as wavelets and Legendre polynomials, are proposed. The extrapolation capacity of existing and proposed encodings is analyzed, extending ALiBi's biasing approach to a unified theoretical context. Experimental evaluation on synthetic sequence-to-sequence tasks shows that orthogonal transform-based encodings outperform traditional sinusoidal encodings in generalization and extrapolation. This work addresses a critical gap in transformer theory, providing insights for design choices in natural language processing, computer vision, and other transformer applications.

Bayesian Attention Mechanism: A Probabilistic Framework for Positional Encoding and Context Length Extrapolation

Transformer-based language models rely on positional encoding (PE) to handle token order and support context length extrapolation. However, existing PE methods lack theoretical clarity and rely on limited evaluation metrics to substantiate their extrapolation claims. We propose the Bayesian Attention Mechanism (BAM), a theoretical framework that formulates positional encoding as a prior within a probabilistic model. BAM unifies existing methods (e.g., NoPE and ALiBi) and motivates a new Generalized Gaussian positional prior that substantially improves long-context generalization. Empirically, BAM enables accurate information retrieval at $500\times$ the training context length, outperforming previous state-of-the-art context length generalization in long context retrieval accuracy while maintaining comparable perplexity and introducing minimal additional parameters.

Context-aware Biases for Length Extrapolation

Transformers' ability to generalize to longer sequences than they have been trained on, known as length extrapolation, degrades as sequence length increases. Most of Relative Positional Encoding (RPE) methods address this problem by either adding constant linear biases or learning general biases, lacking the ability to specialize for different sequences. In this work, inspired by ALiBi, we propose Context-aware Biases for Length Extrapolation (Cable), that learns token-specific biases for each head in decoder-based transformers. Cable learns adaptive, context-aware biases, overcoming the limitations of fixed patterns by adding dynamic biases specific to each token in the sequence. Results show that when tested on a sequence length of 1024, a GPT-3 Medium (334M parameters) with our positional encoding, trained on a sequence length of 512, achieves better perplexity (-0.65) than a similar network with sinusoidal positional encoding trained on a sequence length of 1024. This is achieved with 48% lower memory usage, and only 3.5% higher training time. Furthermore, our method notably improves the extrapolation ability of existing RPE methods on the Edu-FineWeb10B and WikiText-103 datasets. Code is available at: https://github.com/axiomlab/Cable

Sliding Window Attention Training for Efficient Large Language Models

Recent advances in transformer-based Large Language Models (LLMs) have demonstrated remarkable capabilities across various tasks. However, their quadratic computational complexity concerning sequence length remains a significant bottleneck for processing long documents. As a result, many efforts like sparse attention and state space models have been proposed to improve the efficiency of LLMs over long sequences. Though effective, these approaches compromise the performance or introduce structural complexity. This calls for a simple yet efficient model that preserves the fundamental Transformer architecture. To this end, we introduce SWAT, which enables efficient long-context handling via Sliding Window Attention Training. This paper first attributes the inefficiency of Transformers to the attention sink phenomenon resulting from the high variance of softmax operation. Then, we replace softmax with the sigmoid function and utilize a balanced ALiBi and Rotary Position Embedding for efficient information compression and retention. Experiments demonstrate that SWAT achieves SOTA performance compared with state-of-the-art linear recurrent architectures on eight benchmarks. Code is available at https://anonymous.4open.science/r/SWAT-attention.

Wavelet-based Positional Representation for Long Context

In the realm of large-scale language models, a significant challenge arises when extrapolating sequences beyond the maximum allowable length. This is because the model's position embedding mechanisms are limited to positions encountered during training, thus preventing effective representation of positions in longer sequences. We analyzed conventional position encoding methods for long contexts and found the following characteristics. (1) When the representation dimension is regarded as the time axis, Rotary Position Embedding (RoPE) can be interpreted as a restricted wavelet transform using Haar-like wavelets. However, because it uses only a fixed scale parameter, it does not fully exploit the advantages of wavelet transforms, which capture the fine movements of non-stationary signals using multiple scales (window sizes). This limitation could explain why RoPE performs poorly in extrapolation. (2) Previous research as well as our own analysis indicates that Attention with Linear Biases (ALiBi) functions similarly to windowed attention, using windows of varying sizes. However, it has limitations in capturing deep dependencies because it restricts the receptive field of the model. From these insights, we propose a new position representation method that captures multiple scales (i.e., window sizes) by leveraging wavelet transforms without limiting the model's attention field. Experimental results show that this new method improves the performance of the model in both short and long contexts. In particular, our method allows extrapolation of position information without limiting the model's attention field.