L4DR: LiDAR-4DRadar Fusion for Weather-Robust 3D Object Detection

LiDAR-based vision systems are integral for 3D object detection, which is crucial for autonomous navigation. However, they suffer from performance degradation in adverse weather conditions due to the quality deterioration of LiDAR point clouds. Fusing LiDAR with the weather-robust 4D radar sensor is expected to solve this problem. However, the fusion of LiDAR and 4D radar is challenging because they differ significantly in terms of data quality and the degree of degradation in adverse weather. To address these issues, we introduce L4DR, a weather-robust 3D object detection method that effectively achieves LiDAR and 4D Radar fusion. Our L4DR includes Multi-Modal Encoding (MME) and Foreground-Aware Denoising (FAD) technique to reconcile sensor gaps, which is the first exploration of the complementarity of early fusion between LiDAR and 4D radar. Additionally, we design an Inter-Modal and Intra-Modal ({IM}2 ) parallel feature extraction backbone coupled with a Multi-Scale Gated Fusion (MSGF) module to counteract the varying degrees of sensor degradation under adverse weather conditions. Experimental evaluation on a VoD dataset with simulated fog proves that L4DR is more adaptable to changing weather conditions. It delivers a significant performance increase under different fog levels, improving the 3D mAP by up to 18.17% over the traditional LiDAR-only approach. Moreover, the results on the K-Radar dataset validate the consistent performance improvement of L4DR in real-world adverse weather conditions.

Active, anytime-valid risk controlling prediction sets

Rigorously establishing the safety of black-box machine learning models concerning critical risk measures is important for providing guarantees about model behavior. Recently, Bates et. al. (JACM '24) introduced the notion of a risk controlling prediction set (RCPS) for producing prediction sets that are statistically guaranteed low risk from machine learning models. Our method extends this notion to the sequential setting, where we provide guarantees even when the data is collected adaptively, and ensures that the risk guarantee is anytime-valid, i.e., simultaneously holds at all time steps. Further, we propose a framework for constructing RCPSes for active labeling, i.e., allowing one to use a labeling policy that chooses whether to query the true label for each received data point and ensures that the expected proportion of data points whose labels are queried are below a predetermined label budget. We also describe how to use predictors (i.e., the machine learning model for which we provide risk control guarantees) to further improve the utility of our RCPSes by estimating the expected risk conditioned on the covariates. We characterize the optimal choices of label policy and predictor under a fixed label budget and show a regret result that relates the estimation error of the optimal labeling policy and predictor to the wealth process that underlies our RCPSes. Lastly, we present practical ways of formulating label policies and empirically show that our label policies use fewer labels to reach higher utility than naive baseline labeling strategies (e.g., labeling all points, randomly labeling points) on both simulations and real data.

Online multiple testing with e-values

A scientist tests a continuous stream of hypotheses over time in the course of her investigation -- she does not test a predetermined, fixed number of hypotheses. The scientist wishes to make as many discoveries as possible while ensuring the number of false discoveries is controlled -- a well recognized way for accomplishing this is to control the false discovery rate (FDR). Prior methods for FDR control in the online setting have focused on formulating algorithms when specific dependency structures are assumed to exist between the test statistics of each hypothesis. However, in practice, these dependencies often cannot be known beforehand or tested after the fact. Our algorithm, e-LOND, provides FDR control under arbitrary, possibly unknown, dependence. We show that our method is more powerful than existing approaches to this problem through simulations. We also formulate extensions of this algorithm to utilize randomization for increased power, and for constructing confidence intervals in online selective inference.

Risk-limiting Financial Audits via Weighted Sampling without Replacement

We introduce the notion of a risk-limiting financial auditing (RLFA): given $N$ transactions, the goal is to estimate the total misstated monetary fraction~($m^*$) to a given accuracy $\epsilon$, with confidence $1-\delta$. We do this by constructing new confidence sequences (CSs) for the weighted average of $N$ unknown values, based on samples drawn without replacement according to a (randomized) weighted sampling scheme. Using the idea of importance weighting to construct test martingales, we first develop a framework to construct CSs for arbitrary sampling strategies. Next, we develop methods to improve the quality of CSs by incorporating side information about the unknown values associated with each item. We show that when the side information is sufficiently predictive, it can directly drive the sampling. Addressing the case where the accuracy is unknown a priori, we introduce a method that incorporates side information via control variates. Crucially, our construction is adaptive: if the side information is highly predictive of the unknown misstated amounts, then the benefits of incorporating it are significant; but if the side information is uncorrelated, our methods learn to ignore it. Our methods recover state-of-the-art bounds for the special case when the weights are equal, which has already found applications in election auditing. The harder weighted case solves our more challenging problem of AI-assisted financial auditing.

Memory Bounds for the Experts Problem

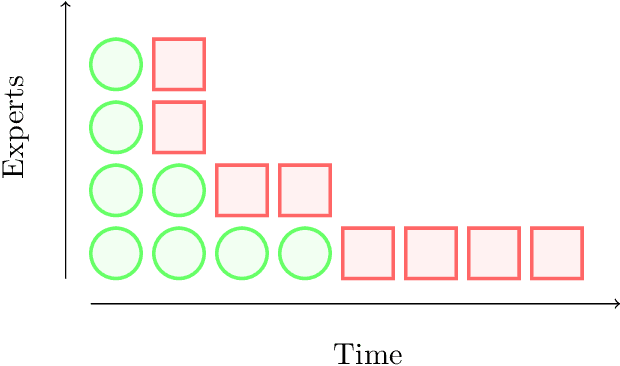
Online learning with expert advice is a fundamental problem of sequential prediction. In this problem, the algorithm has access to a set of $n$ "experts" who make predictions on each day. The goal on each day is to process these predictions, and make a prediction with the minimum cost. After making a prediction, the algorithm sees the actual outcome on that day, updates its state, and then moves on to the next day. An algorithm is judged by how well it does compared to the best expert in the set. The classical algorithm for this problem is the multiplicative weights algorithm. However, every application, to our knowledge, relies on storing weights for every expert, and uses $\Omega(n)$ memory. There is little work on understanding the memory required to solve the online learning with expert advice problem, or run standard sequential prediction algorithms, in natural streaming models, which is especially important when the number of experts, as well as the number of days on which the experts make predictions, is large. We initiate the study of the learning with expert advice problem in the streaming setting, and show lower and upper bounds. Our lower bound for i.i.d., random order, and adversarial order streams uses a reduction to a custom-built problem using a novel masking technique, to show a smooth trade-off for regret versus memory. Our upper bounds show novel ways to run standard sequential prediction algorithms in rounds on small "pools" of experts, thus reducing the necessary memory. For random-order streams, we show that our upper bound is tight up to low order terms. We hope that these results and techniques will have broad applications in online learning, and can inspire algorithms based on standard sequential prediction techniques, like multiplicative weights, for a wide range of other problems in the memory-constrained setting.

A unified framework for bandit multiple testing

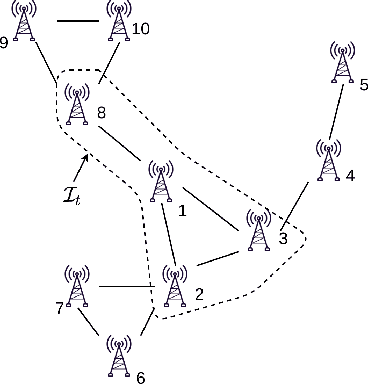
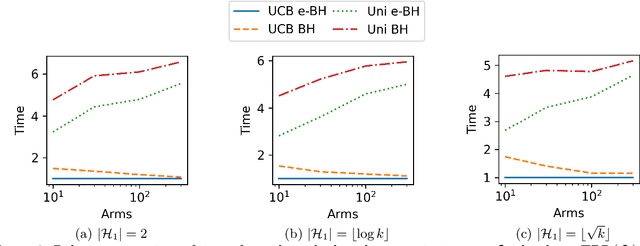
In bandit multiple hypothesis testing, each arm corresponds to a different null hypothesis that we wish to test, and the goal is to design adaptive algorithms that correctly identify large set of interesting arms (true discoveries), while only mistakenly identifying a few uninteresting ones (false discoveries). One common metric in non-bandit multiple testing is the false discovery rate (FDR). We propose a unified, modular framework for bandit FDR control that emphasizes the decoupling of exploration and summarization of evidence. We utilize the powerful martingale-based concept of ``e-processes'' to ensure FDR control for arbitrary composite nulls, exploration rules and stopping times in generic problem settings. In particular, valid FDR control holds even if the reward distributions of the arms could be dependent, multiple arms may be queried simultaneously, and multiple (cooperating or competing) agents may be querying arms, covering combinatorial semi-bandit type settings as well. Prior work has considered in great detail the setting where each arm's reward distribution is independent and sub-Gaussian, and a single arm is queried at each step. Our framework recovers matching sample complexity guarantees in this special case, and performs comparably or better in practice. For other settings, sample complexities will depend on the finer details of the problem (composite nulls being tested, exploration algorithm, data dependence structure, stopping rule) and we do not explore these; our contribution is to show that the FDR guarantee is clean and entirely agnostic to these details.

Dynamic Algorithms for Online Multiple Testing

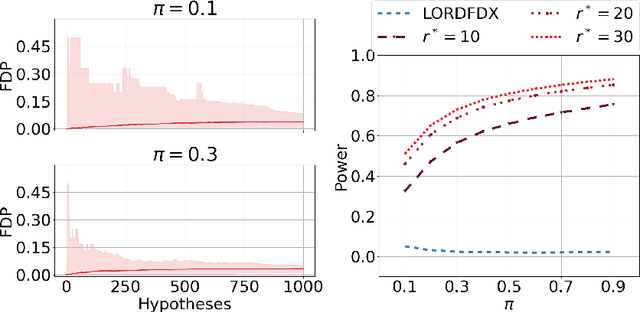
We demonstrate new algorithms for online multiple testing that provably control false discovery exceedance (FDX) while achieving orders of magnitude more power than previous methods. This statistical advance is enabled by the development of new algorithmic ideas: earlier algorithms are more "static" while our new ones allow for the dynamical adjustment of testing levels based on the amount of wealth the algorithm has accumulated. We also prove relationships between controlling FDR, FDX, and other error metrics for our new algorithm, SupLORD, and how controlling one metric can simultaneously control all error metrics. We demonstrate that our algorithms achieve higher power in a variety of synthetic experiments.

Class-Weighted Classification: Trade-offs and Robust Approaches

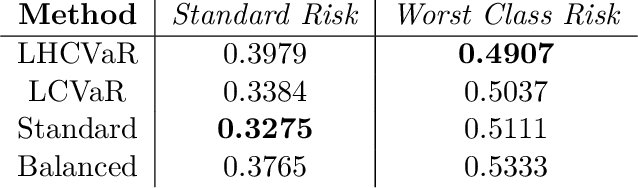
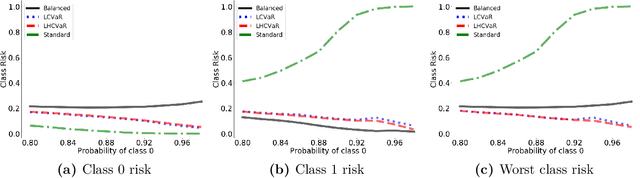
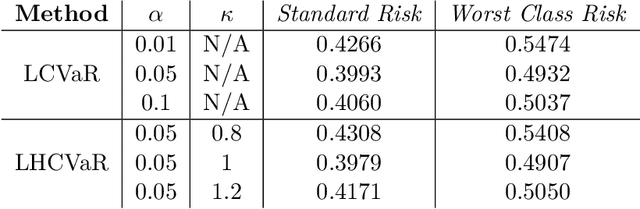
We address imbalanced classification, the problem in which a label may have low marginal probability relative to other labels, by weighting losses according to the correct class. First, we examine the convergence rates of the expected excess weighted risk of plug-in classifiers where the weighting for the plug-in classifier and the risk may be different. This leads to irreducible errors that do not converge to the weighted Bayes risk, which motivates our consideration of robust risks. We define a robust risk that minimizes risk over a set of weightings and show excess risk bounds for this problem. Finally, we show that particular choices of the weighting set leads to a special instance of conditional value at risk (CVaR) from stochastic programming, which we call label conditional value at risk (LCVaR). Additionally, we generalize this weighting to derive a new robust risk problem that we call label heterogeneous conditional value at risk (LHCVaR). Finally, we empirically demonstrate the efficacy of LCVaR and LHCVaR on improving class conditional risks.

Multiclass Classification via Class-Weighted Nearest Neighbors

We study statistical properties of the k-nearest neighbors algorithm for multiclass classification, with a focus on settings where the number of classes may be large and/or classes may be highly imbalanced. In particular, we consider a variant of the k-nearest neighbor classifier with non-uniform class-weightings, for which we derive upper and minimax lower bounds on accuracy, class-weighted risk, and uniform error. Additionally, we show that uniform error bounds lead to bounds on the difference between empirical confusion matrix quantities and their population counterparts across a set of weights. As a result, we may adjust the class weights to optimize classification metrics such as F1 score or Matthew's Correlation Coefficient that are commonly used in practice, particularly in settings with imbalanced classes. We additionally provide a simple example to instantiate our bounds and numerical experiments.