Statistical Theory for Imbalanced Binary Classification

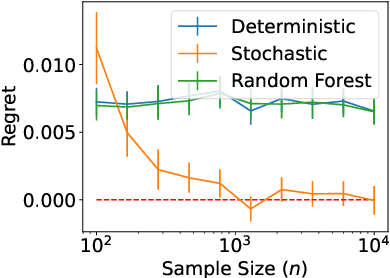
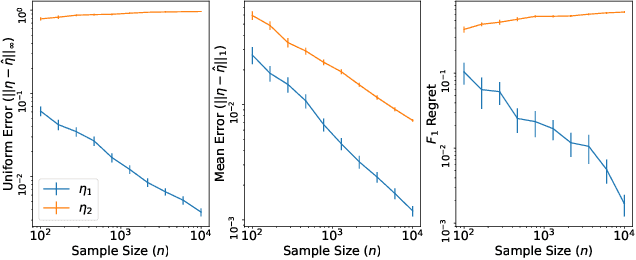
Within the vast body of statistical theory developed for binary classification, few meaningful results exist for imbalanced classification, in which data are dominated by samples from one of the two classes. Existing theory faces at least two main challenges. First, meaningful results must consider more complex performance measures than classification accuracy. To address this, we characterize a novel generalization of the Bayes-optimal classifier to any performance metric computed from the confusion matrix, and we use this to show how relative performance guarantees can be obtained in terms of the error of estimating the class probability function under uniform ($\mathcal{L}_\infty$) loss. Second, as we show, optimal classification performance depends on certain properties of class imbalance that have not previously been formalized. Specifically, we propose a novel sub-type of class imbalance, which we call Uniform Class Imbalance. We analyze how Uniform Class Imbalance influences optimal classifier performance and show that it necessitates different classifier behavior than other types of class imbalance. We further illustrate these two contributions in the case of $k$-nearest neighbor classification, for which we develop novel guarantees. Together, these results provide some of the first meaningful finite-sample statistical theory for imbalanced binary classification.

Class-Weighted Classification: Trade-offs and Robust Approaches

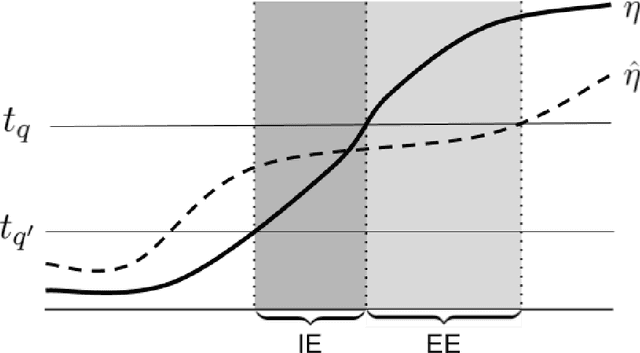
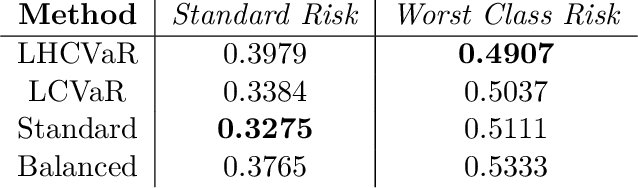
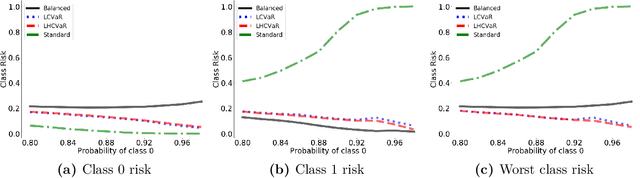
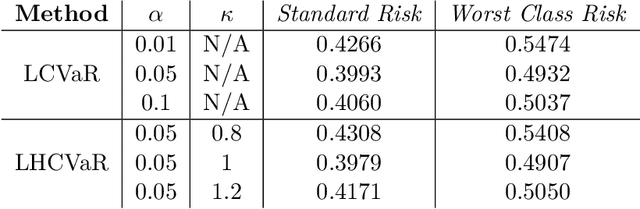
We address imbalanced classification, the problem in which a label may have low marginal probability relative to other labels, by weighting losses according to the correct class. First, we examine the convergence rates of the expected excess weighted risk of plug-in classifiers where the weighting for the plug-in classifier and the risk may be different. This leads to irreducible errors that do not converge to the weighted Bayes risk, which motivates our consideration of robust risks. We define a robust risk that minimizes risk over a set of weightings and show excess risk bounds for this problem. Finally, we show that particular choices of the weighting set leads to a special instance of conditional value at risk (CVaR) from stochastic programming, which we call label conditional value at risk (LCVaR). Additionally, we generalize this weighting to derive a new robust risk problem that we call label heterogeneous conditional value at risk (LHCVaR). Finally, we empirically demonstrate the efficacy of LCVaR and LHCVaR on improving class conditional risks.

Multiclass Classification via Class-Weighted Nearest Neighbors

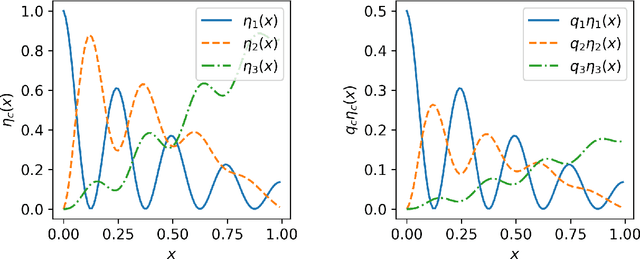
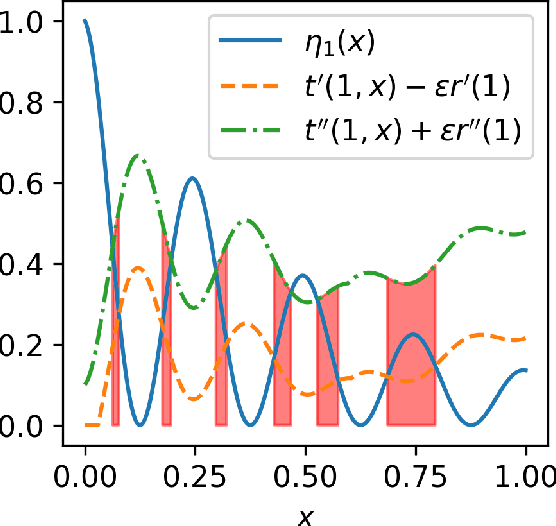
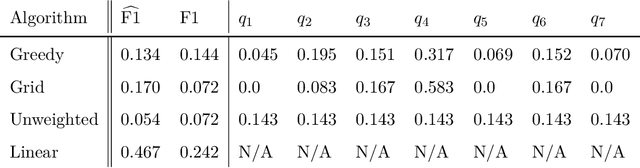
We study statistical properties of the k-nearest neighbors algorithm for multiclass classification, with a focus on settings where the number of classes may be large and/or classes may be highly imbalanced. In particular, we consider a variant of the k-nearest neighbor classifier with non-uniform class-weightings, for which we derive upper and minimax lower bounds on accuracy, class-weighted risk, and uniform error. Additionally, we show that uniform error bounds lead to bounds on the difference between empirical confusion matrix quantities and their population counterparts across a set of weights. As a result, we may adjust the class weights to optimize classification metrics such as F1 score or Matthew's Correlation Coefficient that are commonly used in practice, particularly in settings with imbalanced classes. We additionally provide a simple example to instantiate our bounds and numerical experiments.

Adversarial Risk Bounds for Binary Classification via Function Transformation

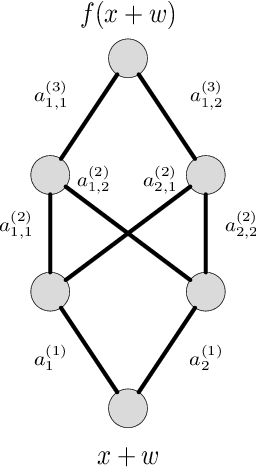
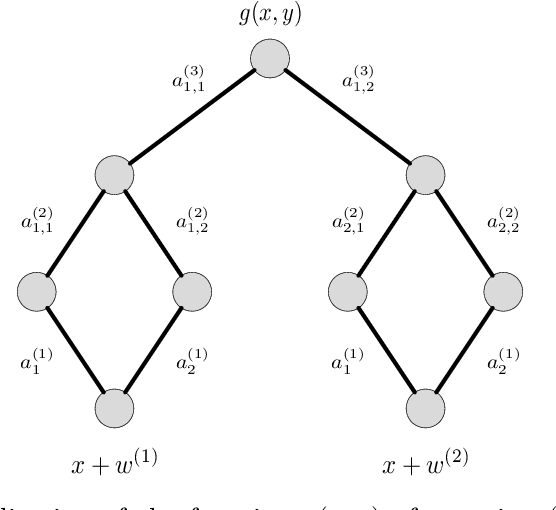
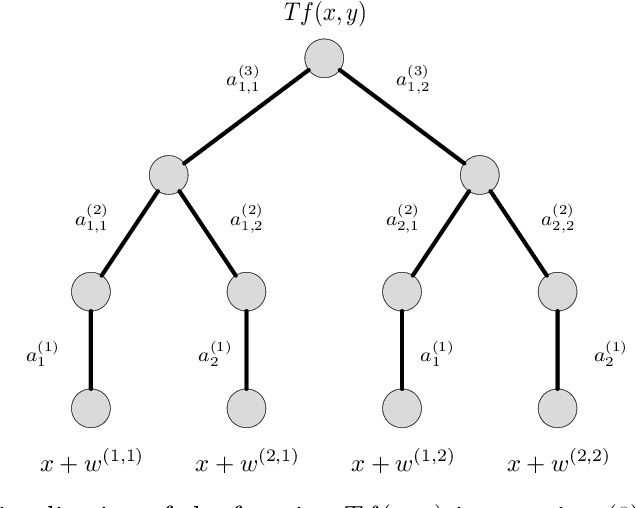
We derive new bounds for a notion of adversarial risk, characterizing the robustness of binary classifiers. Specifically, we study the cases of linear classifiers and neural network classifiers, and introduce transformations with the property that the risk of the transformed functions upper-bounds the adversarial risk of the original functions. This reduces the problem of deriving adversarial risk bounds to the problem of deriving risk bounds using standard learning-theoretic techniques. We then derive bounds on the Rademacher complexities of the transformed function classes, obtaining error rates on the same order as the generalization error of the original function classes. Finally, we provide two algorithms for optimizing the adversarial risk bounds in the linear case, and discuss connections to regularization and distributional robustness.

Computationally Efficient Influence Maximization in Stochastic and Adversarial Models: Algorithms and Analysis

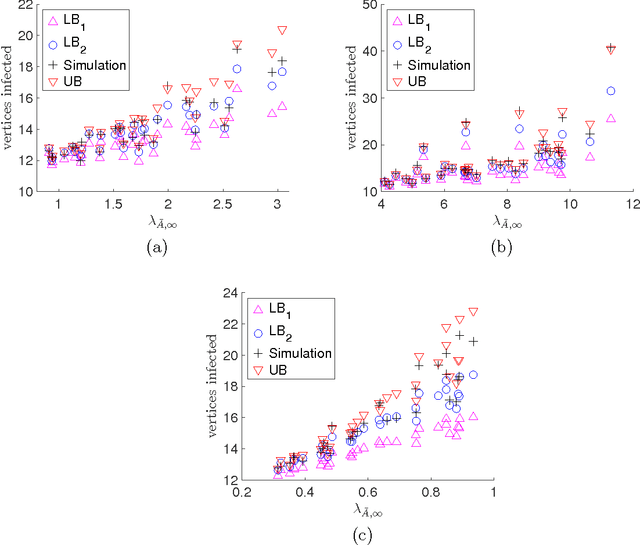
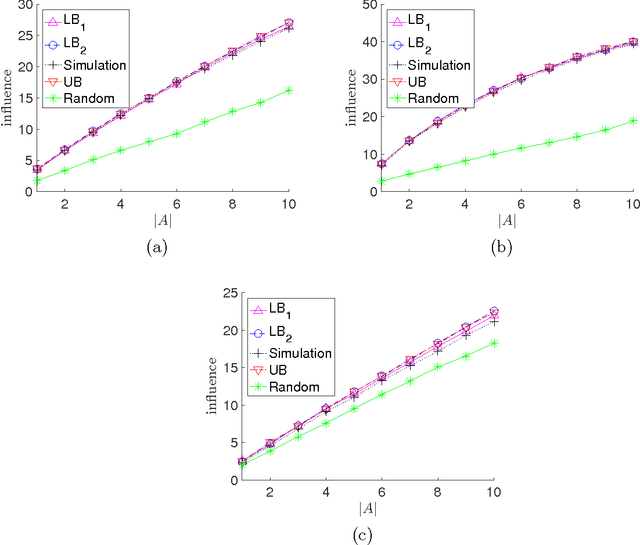
We consider the problem of influence maximization in fixed networks, for both stochastic and adversarial contagion models. The common goal is to select a subset of nodes of a specified size to infect so that the number of infected nodes at the conclusion of the epidemic is as large as possible. In the stochastic setting, the epidemic spreads according to a general triggering model, which includes the popular linear threshold and independent cascade models. We establish upper and lower bounds for the influence of an initial subset of nodes in the network, where the influence is defined as the expected number of infected nodes. Although the problem of exact influence computation is NP-hard in general, our bounds may be evaluated efficiently, leading to scalable algorithms for influence maximization with rigorous theoretical guarantees. In the adversarial spreading setting, an adversary is allowed to specify the edges through which contagion may spread, and the player chooses sets of nodes to infect in successive rounds. Both the adversary and player may behave stochastically, but we limit the adversary to strategies that are oblivious of the player's actions. We establish upper and lower bounds on the minimax pseudo-regret in both undirected and directed networks.

Confidence Sets for the Source of a Diffusion in Regular Trees

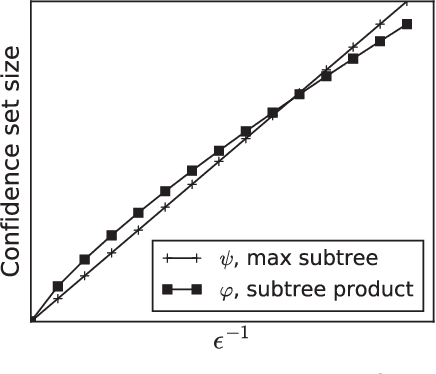
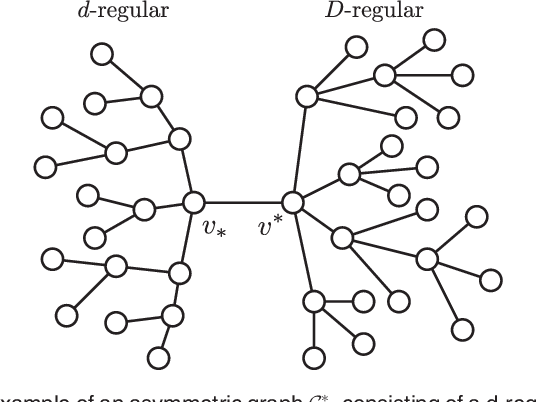
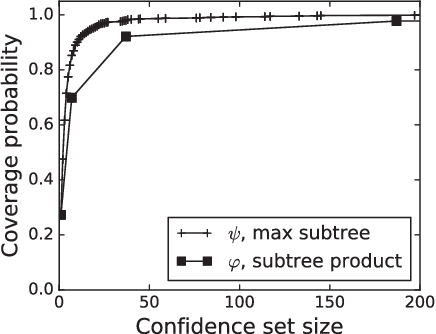
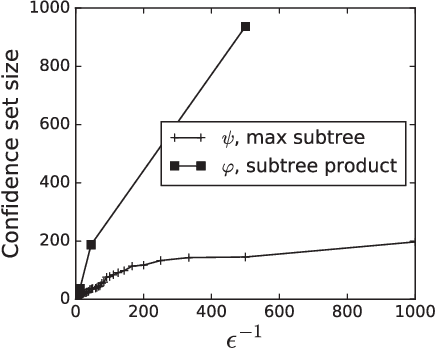
We study the problem of identifying the source of a diffusion spreading over a regular tree. When the degree of each node is at least three, we show that it is possible to construct confidence sets for the diffusion source with size independent of the number of infected nodes. Our estimators are motivated by analogous results in the literature concerning identification of the root node in preferential attachment and uniform attachment trees. At the core of our proofs is a probabilistic analysis of P\'{o}lya urns corresponding to the number of uninfected neighbors in specific subtrees of the infection tree. We also provide an example illustrating the shortcomings of source estimation techniques in settings where the underlying graph is asymmetric.