Efficient Decoder Scaling Strategy for Neural Routing Solvers

Construction-based neural routing solvers, typically composed of an encoder and a decoder, have emerged as a promising approach for solving vehicle routing problems. While recent studies suggest that shifting parameters from the encoder to the decoder enhances performance, most works restrict the decoder size to 1-3M parameters, leaving the effects of scaling largely unexplored. To address this gap, we conduct a systematic study comparing two distinct strategies: scaling depth versus scaling width. We synthesize these strategies to construct a suite of 12 model configurations, spanning a parameter range from 1M to ~150M, and extensively evaluate their scaling behaviors across three critical dimensions: parameter efficiency, data efficiency, and compute efficiency. Our empirical results reveal that parameter count is insufficient to accurately predict the model performance, highlighting the critical and distinct roles of model depth (layer count) and width (embedding dimension). Crucially, we demonstrate that scaling depth yields superior performance gains to scaling width. Based on these findings, we provide and experimentally validate a set of design principles for the efficient allocation of parameters and compute resources to enhance the model performance.

Enhancing CVRP Solver through LLM-driven Automatic Heuristic Design

The Capacitated Vehicle Routing Problem (CVRP), a fundamental combinatorial optimization challenge, focuses on optimizing fleet operations under vehicle capacity constraints. While extensively studied in operational research, the NP-hard nature of CVRP continues to pose significant computational challenges, particularly for large-scale instances. This study presents AILS-AHD (Adaptive Iterated Local Search with Automatic Heuristic Design), a novel approach that leverages Large Language Models (LLMs) to revolutionize CVRP solving. Our methodology integrates an evolutionary search framework with LLMs to dynamically generate and optimize ruin heuristics within the AILS method. Additionally, we introduce an LLM-based acceleration mechanism to enhance computational efficiency. Comprehensive experimental evaluations against state-of-the-art solvers, including AILS-II and HGS, demonstrate the superior performance of AILS-AHD across both moderate and large-scale instances. Notably, our approach establishes new best-known solutions for 8 out of 10 instances in the CVRPLib large-scale benchmark, underscoring the potential of LLM-driven heuristic design in advancing the field of vehicle routing optimization.

Survey on Neural Routing Solvers

Neural routing solvers (NRSs) that leverage deep learning to tackle vehicle routing problems have demonstrated notable potential for practical applications. By learning implicit heuristic rules from data, NRSs replace the handcrafted counterparts in classic heuristic frameworks, thereby reducing reliance on costly manual design and trial-and-error adjustments. This survey makes two main contributions: (1) The heuristic nature of NRSs is highlighted, and existing NRSs are reviewed from the perspective of heuristics. A hierarchical taxonomy based on heuristic principles is further introduced. (2) A generalization-focused evaluation pipeline is proposed to address limitations of the conventional pipeline. Comparative benchmarking of representative NRSs across both pipelines uncovers a series of previously unreported gaps in current research.

Look Before Switch: Sensing-Assisted Handover in 5G NR V2I Networks

Integrated Sensing and Communication (ISAC) has emerged as a promising solution in addressing the challenges of high-mobility scenarios in 5G NR Vehicle-to-Infrastructure (V2I) communications. This paper proposes a novel sensing-assisted handover framework that leverages ISAC capabilities to enable precise beamforming and proactive handover decisions. Two sensing-enabled handover triggering algorithms are developed: a distance-based scheme that utilizes estimated spatial positioning, and a probability-based approach that predicts vehicle maneuvers using interacting multiple model extended Kalman filter (IMM-EKF) tracking. The proposed methods eliminate the need for uplink feedback and beam sweeping, thus significantly reducing signaling overhead and handover interruption time. A sensing-assisted NR frame structure and corresponding protocol design are also introduced to support rapid synchronization and access under vehicular mobility. Extensive link-level simulations using real-world map data demonstrate that the proposed framework reduces the average handover interruption time by over 50%, achieves lower handover rates, and enhances overall communication performance.

Rethinking Neural Combinatorial Optimization for Vehicle Routing Problems with Different Constraint Tightness Degrees

Recent neural combinatorial optimization (NCO) methods have shown promising problem-solving ability without requiring domain-specific expertise. Most existing NCO methods use training and testing data with a fixed constraint value and lack research on the effect of constraint tightness on the performance of NCO methods. This paper takes the capacity-constrained vehicle routing problem (CVRP) as an example to empirically analyze the NCO performance under different tightness degrees of the capacity constraint. Our analysis reveals that existing NCO methods overfit the capacity constraint, and they can only perform satisfactorily on a small range of the constraint values but poorly on other values. To tackle this drawback of existing NCO methods, we develop an efficient training scheme that explicitly considers varying degrees of constraint tightness and proposes a multi-expert module to learn a generally adaptable solving strategy. Experimental results show that the proposed method can effectively overcome the overfitting issue, demonstrating superior performances on the CVRP and CVRP with time windows (CVRPTW) with various constraint tightness degrees.

Enhanced Ideal Objective Vector Estimation for Evolutionary Multi-Objective Optimization

The ideal objective vector, which comprises the optimal values of the $m$ objective functions in an $m$-objective optimization problem, is an important concept in evolutionary multi-objective optimization. Accurate estimation of this vector has consistently been a crucial task, as it is frequently used to guide the search process and normalize the objective space. Prevailing estimation methods all involve utilizing the best value concerning each objective function achieved by the individuals in the current or accumulated population. However, this paper reveals that the population-based estimation method can only work on simple problems but falls short on problems with substantial bias. The biases in multi-objective optimization problems can be divided into three categories, and an analysis is performed to illustrate how each category hinders the estimation of the ideal objective vector. Subsequently, a set of test instances is proposed to quantitatively evaluate the impact of various biases on the ideal objective vector estimation method. Beyond that, a plug-and-play component called enhanced ideal objective vector estimation (EIE) is introduced for multi-objective evolutionary algorithms (MOEAs). EIE features adaptive and fine-grained searches over $m$ subproblems defined by the extreme weighted sum method. EIE finally outputs $m$ solutions that can well approximate the ideal objective vector. In the experiments, EIE is integrated into three representative MOEAs. To demonstrate the wide applicability of EIE, algorithms are tested not only on the newly proposed test instances but also on existing ones. The results consistently show that EIE improves the ideal objective vector estimation and enhances the MOEA's performance.

Weak Pareto Boundary: The Achilles' Heel of Evolutionary Multi-Objective Optimization

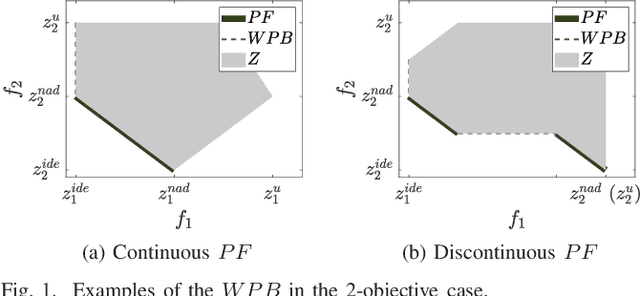
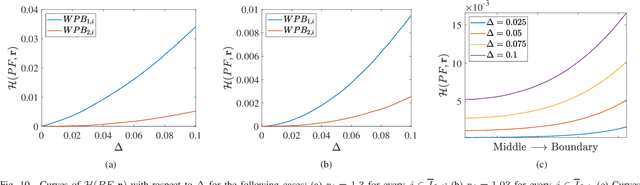
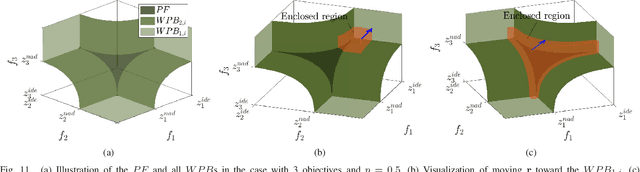
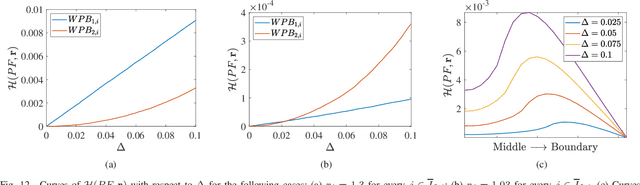
The weak Pareto boundary ($WPB$) refers to a boundary in the objective space of a multi-objective optimization problem, characterized by weak Pareto optimality rather than Pareto optimality. The $WPB$ brings severe challenges to multi-objective evolutionary algorithms (MOEAs), as it may mislead the algorithms into finding dominance-resistant solutions (DRSs), i.e., solutions that excel on some objectives but severely underperform on the others, thereby missing Pareto-optimal solutions. Although the severe impact of the $WPB$ on MOEAs has been recognized, a systematic and detailed analysis remains lacking. To fill this gap, this paper studies the attributes of the $WPB$. In particular, the category of a $WPB$, as an attribute derived from its weakly Pareto-optimal property, is theoretically analyzed. The analysis reveals that the dominance resistance degrees of DRSs induced by different categories of $WPB$s exhibit distinct asymptotic growth rates as the DRSs in the objective space approach the $WPB$s, where a steeper asymptotic growth rate indicates a greater hindrance to MOEAs. Beyond that, experimental studies are conducted on various new test problems to investigate the impact of $WPB$'s attributes. The experimental results demonstrate consistency with our theoretical findings. Experiments on other attributes show that the performance of an MOEA is highly sensitive to some attributes. Overall, no existing MOEAs can comprehensively address challenges brought by these attributes.

Learning to Insert for Constructive Neural Vehicle Routing Solver

Neural Combinatorial Optimisation (NCO) is a promising learning-based approach for solving Vehicle Routing Problems (VRPs) without extensive manual design. While existing constructive NCO methods typically follow an appending-based paradigm that sequentially adds unvisited nodes to partial solutions, this rigid approach often leads to suboptimal results. To overcome this limitation, we explore the idea of insertion-based paradigm and propose Learning to Construct with Insertion-based Paradigm (L2C-Insert), a novel learning-based method for constructive NCO. Unlike traditional approaches, L2C-Insert builds solutions by strategically inserting unvisited nodes at any valid position in the current partial solution, which can significantly enhance the flexibility and solution quality. The proposed framework introduces three key components: a novel model architecture for precise insertion position prediction, an efficient training scheme for model optimization, and an advanced inference technique that fully exploits the insertion paradigm's flexibility. Extensive experiments on both synthetic and real-world instances of the Travelling Salesman Problem (TSP) and Capacitated Vehicle Routing Problem (CVRP) demonstrate that L2C-Insert consistently achieves superior performance across various problem sizes.

L2R: Learning to Reduce Search Space for Generalizable Neural Routing Solver

Constructive neural combinatorial optimization (NCO) has attracted growing research attention due to its ability to solve complex routing problems without relying on handcrafted rules. However, existing NCO methods face significant challenges in generalizing to large-scale problems due to high computational complexity and inefficient capture of structural patterns. To address this issue, we propose a novel learning-based search space reduction method that adaptively selects a small set of promising candidate nodes at each step of the constructive NCO process. Unlike traditional methods that rely on fixed heuristics, our selection model dynamically prioritizes nodes based on learned patterns, significantly reducing the search space while maintaining solution quality. Experimental results demonstrate that our method, trained solely on 100-node instances from uniform distribution, generalizes remarkably well to large-scale Traveling Salesman Problem (TSP) and Capacitated Vehicle Routing Problem (CVRP) instances with up to 1 million nodes from the uniform distribution and over 80K nodes from other distributions.

ARS: Automatic Routing Solver with Large Language Models

Real-world Vehicle Routing Problems (VRPs) are characterized by a variety of practical constraints, making manual solver design both knowledge-intensive and time-consuming. Although there is increasing interest in automating the design of routing algorithms, existing research has explored only a limited array of VRP variants and fails to adequately address the complex and prevalent constraints encountered in real-world situations. To fill this gap, this paper introduces RoutBench, a benchmark of 1,000 VRP variants derived from 24 attributes, for evaluating the effectiveness of automatic routing solvers in addressing complex constraints. Along with RoutBench, we present the Automatic Routing Solver (ARS), which employs Large Language Model (LLM) agents to enhance a backbone algorithm framework by automatically generating constraint-aware heuristic code, based on problem descriptions and several representative constraints selected from a database. Our experiments show that ARS outperforms state-of-the-art LLM-based methods and commonly used solvers, automatically solving 91.67% of common VRPs and achieving at least a 30% improvement across all benchmarks.