DeReason: A Difficulty-Aware Curriculum Improves Decoupled SFT-then-RL Training for General Reasoning

Reinforcement learning with Verifiable Rewards (RLVR) has emerged as a powerful paradigm for eliciting reasoning capabilities in large language models, particularly in mathematics and coding. While recent efforts have extended this paradigm to broader general scientific (STEM) domains, the complex interplay between supervised fine-tuning (SFT) and RL in these contexts remains underexplored. In this paper, we conduct controlled experiments revealing a critical challenge: for general STEM domains, RL applied directly to base models is highly sample-inefficient and is consistently surpassed by supervised fine-tuning (SFT) on moderate-quality responses. Yet sequential SFT followed by RL can further improve performance, suggesting that the two stages play complementary roles, and that how training data is allocated between them matters. Therefore, we propose DeReason, a difficulty-based data decoupling strategy for general reasoning. DeReason partitions training data by reasoning intensity estimated via LLM-based scoring into reasoning-intensive and non-reasoning-intensive subsets. It allocates broad-coverage, non-reasoning-intensive problems to SFT to establish foundational domain knowledge, and reserves a focused subset of difficult problems for RL to cultivate complex reasoning. We demonstrate that this principled decoupling yields better performance than randomly splitting the data for sequential SFT and RL. Extensive experiments on general STEM and mathematical benchmarks demonstrate that our decoupled curriculum training significantly outperforms SFT-only, RL-only, and random-split baselines. Our work provides a systematic study of the interplay between SFT and RL for general reasoning, offering a highly effective and generalized post-training recipe.

Accordion-Thinking: Self-Regulated Step Summaries for Efficient and Readable LLM Reasoning

Scaling test-time compute via long Chain-ofThought unlocks remarkable gains in reasoning capabilities, yet it faces practical limits due to the linear growth of KV cache and quadratic attention complexity. In this paper, we introduce Accordion-Thinking, an end-to-end framework where LLMs learn to self-regulate the granularity of the reasoning steps through dynamic summarization. This mechanism enables a Fold inference mode, where the model periodically summarizes its thought process and discards former thoughts to reduce dependency on historical tokens. We apply reinforcement learning to incentivize this capability further, uncovering a critical insight: the accuracy gap between the highly efficient Fold mode and the exhaustive Unfold mode progressively narrows and eventually vanishes over the course of training. This phenomenon demonstrates that the model learns to encode essential reasoning information into compact summaries, achieving effective compression of the reasoning context. Our Accordion-Thinker demonstrates that with learned self-compression, LLMs can tackle complex reasoning tasks with minimal dependency token overhead without compromising solution quality, and it achieves a 3x throughput while maintaining accuracy on a 48GB GPU memory configuration, while the structured step summaries provide a human-readable account of the reasoning process.

Uncovering Hidden Correctness in LLM Causal Reasoning via Symbolic Verification

Large language models (LLMs) are increasingly being applied to tasks that involve causal reasoning. However, current benchmarks often rely on string matching or surface-level metrics that do not capture whether the output of a model is formally valid under the semantics of causal reasoning. To address this, we propose DoVerifier, a simple symbolic verifier that checks whether LLM-generated causal expressions are derivable from a given causal graph using rules from do-calculus and probability theory. This allows us to recover correct answers to causal queries that would otherwise be marked incorrect due to superficial differences in their causal semantics. Our evaluations on synthetic data and causal QA benchmarks show that DoVerifier more accurately captures semantic correctness of causal reasoning traces, offering a more rigorous and informative way to evaluate LLMs on causal reasoning.

Aligning Perception, Reasoning, Modeling and Interaction: A Survey on Physical AI

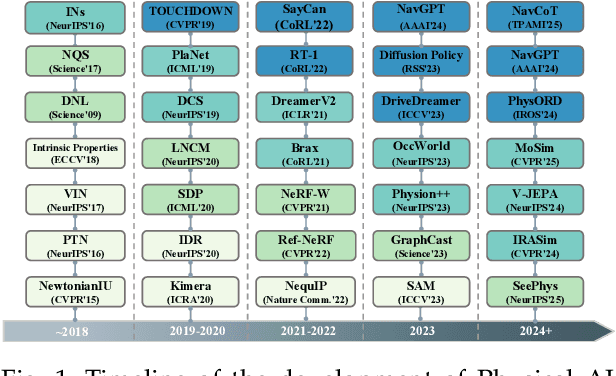
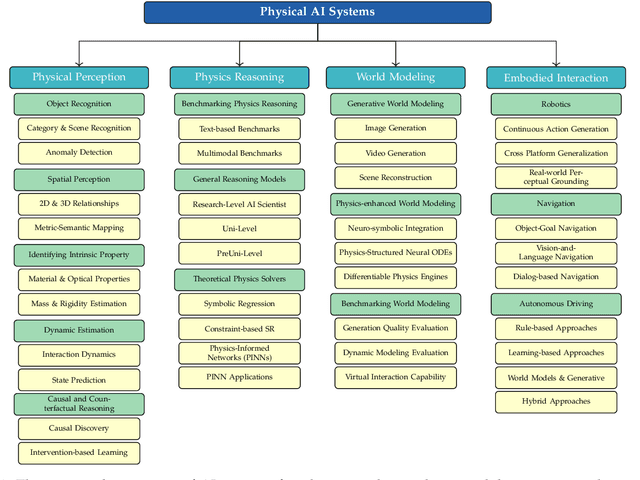
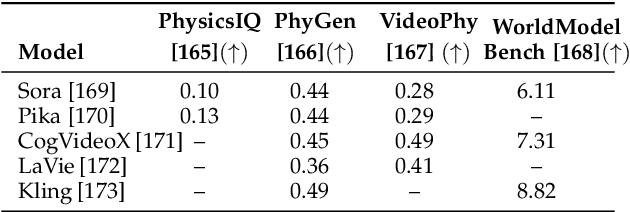
The rapid advancement of embodied intelligence and world models has intensified efforts to integrate physical laws into AI systems, yet physical perception and symbolic physics reasoning have developed along separate trajectories without a unified bridging framework. This work provides a comprehensive overview of physical AI, establishing clear distinctions between theoretical physics reasoning and applied physical understanding while systematically examining how physics-grounded methods enhance AI's real-world comprehension across structured symbolic reasoning, embodied systems, and generative models. Through rigorous analysis of recent advances, we advocate for intelligent systems that ground learning in both physical principles and embodied reasoning processes, transcending pattern recognition toward genuine understanding of physical laws. Our synthesis envisions next-generation world models capable of explaining physical phenomena and predicting future states, advancing safe, generalizable, and interpretable AI systems. We maintain a continuously updated resource at https://github.com/AI4Phys/Awesome-AI-for-Physics.

TreeRPO: Tree Relative Policy Optimization

Large Language Models (LLMs) have shown remarkable reasoning capabilities through Reinforcement Learning with Verifiable Rewards (RLVR) methods. However, a key limitation of existing approaches is that rewards defined at the full trajectory level provide insufficient guidance for optimizing the intermediate steps of a reasoning process. To address this, we introduce \textbf{\name}, a novel method that estimates the mathematical expectations of rewards at various reasoning steps using tree sampling. Unlike prior methods that rely on a separate step reward model, \name directly estimates these rewards through this sampling process. Building on the group-relative reward training mechanism of GRPO, \name innovatively computes rewards based on step-level groups generated during tree sampling. This advancement allows \name to produce fine-grained and dense reward signals, significantly enhancing the learning process and overall performance of LLMs. Experimental results demonstrate that our \name algorithm substantially improves the average Pass@1 accuracy of Qwen-2.5-Math on test benchmarks, increasing it from 19.0\% to 35.5\%. Furthermore, \name significantly outperforms GRPO by 2.9\% in performance while simultaneously reducing the average response length by 18.1\%, showcasing its effectiveness and efficiency. Our code will be available at \href{https://github.com/yangzhch6/TreeRPO}{https://github.com/yangzhch6/TreeRPO}.

SeePhys: Does Seeing Help Thinking? -- Benchmarking Vision-Based Physics Reasoning

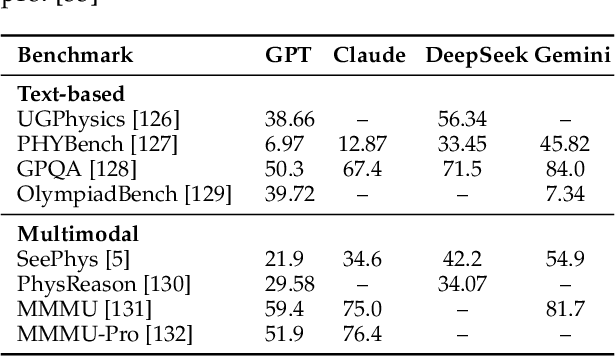
We present SeePhys, a large-scale multimodal benchmark for LLM reasoning grounded in physics questions ranging from middle school to PhD qualifying exams. The benchmark covers 7 fundamental domains spanning the physics discipline, incorporating 21 categories of highly heterogeneous diagrams. In contrast to prior works where visual elements mainly serve auxiliary purposes, our benchmark features a substantial proportion of vision-essential problems (75\%) that mandate visual information extraction for correct solutions. Through extensive evaluation, we observe that even the most advanced visual reasoning models (e.g., Gemini-2.5-pro and o4-mini) achieve sub-60\% accuracy on our benchmark. These results reveal fundamental challenges in current large language models' visual understanding capabilities, particularly in: (i) establishing rigorous coupling between diagram interpretation and physics reasoning, and (ii) overcoming their persistent reliance on textual cues as cognitive shortcuts.

LEXam: Benchmarking Legal Reasoning on 340 Law Exams

Long-form legal reasoning remains a key challenge for large language models (LLMs) in spite of recent advances in test-time scaling. We introduce LEXam, a novel benchmark derived from 340 law exams spanning 116 law school courses across a range of subjects and degree levels. The dataset comprises 4,886 law exam questions in English and German, including 2,841 long-form, open-ended questions and 2,045 multiple-choice questions. Besides reference answers, the open questions are also accompanied by explicit guidance outlining the expected legal reasoning approach such as issue spotting, rule recall, or rule application. Our evaluation on both open-ended and multiple-choice questions present significant challenges for current LLMs; in particular, they notably struggle with open questions that require structured, multi-step legal reasoning. Moreover, our results underscore the effectiveness of the dataset in differentiating between models with varying capabilities. Adopting an LLM-as-a-Judge paradigm with rigorous human expert validation, we demonstrate how model-generated reasoning steps can be evaluated consistently and accurately. Our evaluation setup provides a scalable method to assess legal reasoning quality beyond simple accuracy metrics. Project page: https://lexam-benchmark.github.io/

FormalAlign: Automated Alignment Evaluation for Autoformalization

Autoformalization aims to convert informal mathematical proofs into machine-verifiable formats, bridging the gap between natural and formal languages. However, ensuring semantic alignment between the informal and formalized statements remains challenging. Existing approaches heavily rely on manual verification, hindering scalability. To address this, we introduce \textsc{FormalAlign}, the first automated framework designed for evaluating the alignment between natural and formal languages in autoformalization. \textsc{FormalAlign} trains on both the autoformalization sequence generation task and the representational alignment between input and output, employing a dual loss that combines a pair of mutually enhancing autoformalization and alignment tasks. Evaluated across four benchmarks augmented by our proposed misalignment strategies, \textsc{FormalAlign} demonstrates superior performance. In our experiments, \textsc{FormalAlign} outperforms GPT-4, achieving an Alignment-Selection Score 11.58\% higher on \forml-Basic (99.21\% vs. 88.91\%) and 3.19\% higher on MiniF2F-Valid (66.39\% vs. 64.34\%). This effective alignment evaluation significantly reduces the need for manual verification. Both the dataset and code can be accessed via~\url{https://github.com/rookie-joe/FormalAlign}.

Benchmarking LLMs for Optimization Modeling and Enhancing Reasoning via Reverse Socratic Synthesis

Large language models (LLMs) have exhibited their problem-solving ability in mathematical reasoning. Solving realistic optimization (OPT) problems in industrial application scenarios requires advanced and applied math ability. However, current OPT benchmarks that merely solve linear programming are far from complex realistic situations. In this work, we propose E-OPT, a benchmark for end-to-end optimization problem-solving with human-readable inputs and outputs. E-OPT contains rich optimization problems, including linear/nonlinear programming with/without table data, which can comprehensively evaluate LLMs' solving ability. In our benchmark, LLMs are required to correctly understand the problem in E-OPT and call code solver to get precise numerical answers. Furthermore, to alleviate the data scarcity for optimization problems, and to bridge the gap between open-source LLMs on a small scale (e.g., Llama-2-7b and Llama-3-8b) and closed-source LLMs (e.g., GPT-4), we further propose a novel data synthesis method namely ReSocratic. Unlike general data synthesis methods that proceed from questions to answers, ReSocratic first incrementally synthesizes optimization scenarios with mathematical formulations step by step and then back-translates the generated scenarios into questions. In such a way, we construct the ReSocratic-29k dataset from a small seed sample pool with the powerful open-source large model DeepSeek-V2. To demonstrate the effectiveness of ReSocratic, we conduct supervised fine-tuning with ReSocratic-29k on multiple open-source models. The results show that Llama3-8b is significantly improved from 13.6% to 51.7% on E-OPT, while DeepSeek-V2 reaches 61.0%, approaching 65.5% of GPT-4.

FVEL: Interactive Formal Verification Environment with Large Language Models via Theorem Proving

Formal verification (FV) has witnessed growing significance with current emerging program synthesis by the evolving large language models (LLMs). However, current formal verification mainly resorts to symbolic verifiers or hand-craft rules, resulting in limitations for extensive and flexible verification. On the other hand, formal languages for automated theorem proving, such as Isabelle, as another line of rigorous verification, are maintained with comprehensive rules and theorems. In this paper, we propose FVEL, an interactive Formal Verification Environment with LLMs. Specifically, FVEL transforms a given code to be verified into Isabelle, and then conducts verification via neural automated theorem proving with an LLM. The joined paradigm leverages the rigorous yet abundant formulated and organized rules in Isabelle and is also convenient for introducing and adjusting cutting-edge LLMs. To achieve this goal, we extract a large-scale FVELER3. The FVELER dataset includes code dependencies and verification processes that are formulated in Isabelle, containing 758 theories, 29,125 lemmas, and 200,646 proof steps in total with in-depth dependencies. We benchmark FVELER in the FVEL environment by first fine-tuning LLMs with FVELER and then evaluating them on Code2Inv and SV-COMP. The results show that FVEL with FVELER fine-tuned Llama3- 8B solves 17.39% (69 -> 81) more problems, and Mistral-7B 12% (75 -> 84) more problems in SV-COMP. And the proportion of proof errors is reduced. Project page: https://fveler.github.io/.