Shiyin Lu
Deep But Reliable: Advancing Multi-turn Reasoning for Thinking with Images
Dec 19, 2025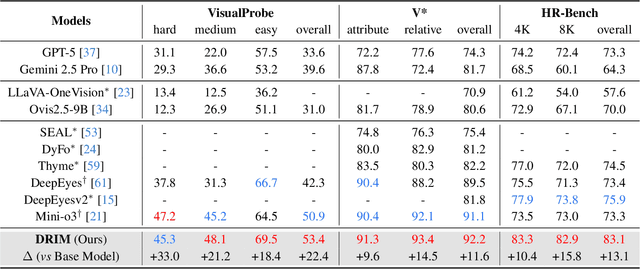
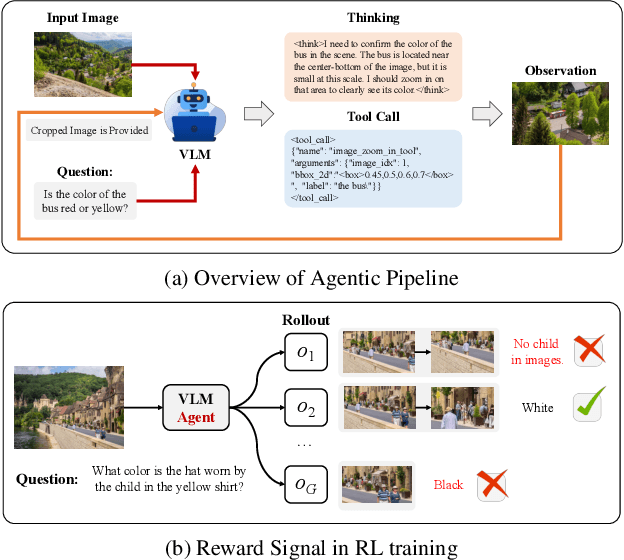
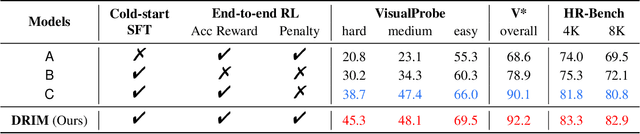
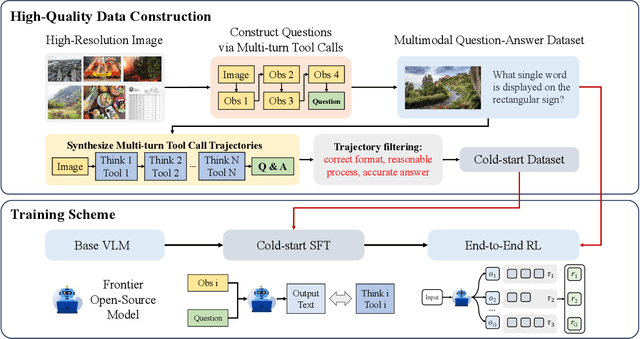
Abstract:Recent advances in large Vision-Language Models (VLMs) have exhibited strong reasoning capabilities on complex visual tasks by thinking with images in their Chain-of-Thought (CoT), which is achieved by actively invoking tools to analyze visual inputs rather than merely perceiving them. However, existing models often struggle to reflect on and correct themselves when attempting incorrect reasoning trajectories. To address this limitation, we propose DRIM, a model that enables deep but reliable multi-turn reasoning when thinking with images in its multimodal CoT. Our pipeline comprises three stages: data construction, cold-start SFT and RL. Based on a high-resolution image dataset, we construct high-difficulty and verifiable visual question-answer pairs, where solving each task requires multi-turn tool calls to reach the correct answer. In the SFT stage, we collect tool trajectories as cold-start data, guiding a multi-turn reasoning pattern. In the RL stage, we introduce redundancy-penalized policy optimization, which incentivizes the model to develop a self-reflective reasoning pattern. The basic idea is to impose judgment on reasoning trajectories and penalize those that produce incorrect answers without sufficient multi-scale exploration. Extensive experiments demonstrate that DRIM achieves superior performance on visual understanding benchmarks.
LPO: Towards Accurate GUI Agent Interaction via Location Preference Optimization
Jun 11, 2025



Abstract:The advent of autonomous agents is transforming interactions with Graphical User Interfaces (GUIs) by employing natural language as a powerful intermediary. Despite the predominance of Supervised Fine-Tuning (SFT) methods in current GUI agents for achieving spatial localization, these methods face substantial challenges due to their limited capacity to accurately perceive positional data. Existing strategies, such as reinforcement learning, often fail to assess positional accuracy effectively, thereby restricting their utility. In response, we introduce Location Preference Optimization (LPO), a novel approach that leverages locational data to optimize interaction preferences. LPO uses information entropy to predict interaction positions by focusing on zones rich in information. Besides, it further introduces a dynamic location reward function based on physical distance, reflecting the varying importance of interaction positions. Supported by Group Relative Preference Optimization (GRPO), LPO facilitates an extensive exploration of GUI environments and significantly enhances interaction precision. Comprehensive experiments demonstrate LPO's superior performance, achieving SOTA results across both offline benchmarks and real-world online evaluations. Our code will be made publicly available soon, at https://github.com/AIDC-AI/LPO.
Multimodal Tabular Reasoning with Privileged Structured Information
Jun 04, 2025Abstract:Tabular reasoning involves multi-step information extraction and logical inference over tabular data. While recent advances have leveraged large language models (LLMs) for reasoning over structured tables, such high-quality textual representations are often unavailable in real-world settings, where tables typically appear as images. In this paper, we tackle the task of tabular reasoning from table images, leveraging privileged structured information available during training to enhance multimodal large language models (MLLMs). The key challenges lie in the complexity of accurately aligning structured information with visual representations, and in effectively transferring structured reasoning skills to MLLMs despite the input modality gap. To address these, we introduce TabUlar Reasoning with Bridged infOrmation ({\sc Turbo}), a new framework for multimodal tabular reasoning with privileged structured tables. {\sc Turbo} benefits from a structure-aware reasoning trace generator based on DeepSeek-R1, contributing to high-quality modality-bridged data. On this basis, {\sc Turbo} repeatedly generates and selects the advantageous reasoning paths, further enhancing the model's tabular reasoning ability. Experimental results demonstrate that, with limited ($9$k) data, {\sc Turbo} achieves state-of-the-art performance ($+7.2\%$ vs. previous SOTA) across multiple datasets.
MDP3: A Training-free Approach for List-wise Frame Selection in Video-LLMs
Jan 06, 2025Abstract:Video large language models (Video-LLMs) have made significant progress in understanding videos. However, processing multiple frames leads to lengthy visual token sequences, presenting challenges such as the limited context length cannot accommodate the entire video, and the inclusion of irrelevant frames hinders visual perception. Hence, effective frame selection is crucial. This paper emphasizes that frame selection should follow three key principles: query relevance, list-wise diversity, and sequentiality. Existing methods, such as uniform frame sampling and query-frame matching, do not capture all of these principles. Thus, we propose Markov decision determinantal point process with dynamic programming (MDP3) for frame selection, a training-free and model-agnostic method that can be seamlessly integrated into existing Video-LLMs. Our method first estimates frame similarities conditioned on the query using a conditional Gaussian kernel within the reproducing kernel Hilbert space~(RKHS). We then apply the determinantal point process~(DPP) to the similarity matrix to capture both query relevance and list-wise diversity. To incorporate sequentiality, we segment the video and apply DPP within each segment, conditioned on the preceding segment selection, modeled as a Markov decision process~(MDP) for allocating selection sizes across segments. Theoretically, MDP3 provides a \((1 - 1/e)\)-approximate solution to the NP-hard list-wise frame selection problem with pseudo-polynomial time complexity, demonstrating its efficiency. Empirically, MDP3 significantly outperforms existing methods, verifying its effectiveness and robustness.
OmniEvalKit: A Modular, Lightweight Toolbox for Evaluating Large Language Model and its Omni-Extensions
Dec 09, 2024Abstract:The rapid advancements in Large Language Models (LLMs) have significantly expanded their applications, ranging from multilingual support to domain-specific tasks and multimodal integration. In this paper, we present OmniEvalKit, a novel benchmarking toolbox designed to evaluate LLMs and their omni-extensions across multilingual, multidomain, and multimodal capabilities. Unlike existing benchmarks that often focus on a single aspect, OmniEvalKit provides a modular, lightweight, and automated evaluation system. It is structured with a modular architecture comprising a Static Builder and Dynamic Data Flow, promoting the seamless integration of new models and datasets. OmniEvalKit supports over 100 LLMs and 50 evaluation datasets, covering comprehensive evaluations across thousands of model-dataset combinations. OmniEvalKit is dedicated to creating an ultra-lightweight and fast-deployable evaluation framework, making downstream applications more convenient and versatile for the AI community.
Wings: Learning Multimodal LLMs without Text-only Forgetting
Jun 05, 2024



Abstract:Multimodal large language models (MLLMs), initiated with a trained LLM, first align images with text and then fine-tune on multimodal mixed inputs. However, the MLLM catastrophically forgets the text-only instructions, which do not include images and can be addressed within the initial LLM. In this paper, we present Wings, a novel MLLM that excels in both text-only dialogues and multimodal comprehension. Analyzing MLLM attention in multimodal instructions reveals that text-only forgetting is related to the attention shifts from pre-image to post-image text. From that, we construct extra modules that act as the boosted learner to compensate for the attention shift. The complementary visual and textual learners, like "wings" on either side, are connected in parallel within each layer's attention block. Initially, image and text inputs are aligned with visual learners operating alongside the main attention, balancing focus on visual elements. Textual learners are later collaboratively integrated with attention-based routing to blend the outputs of the visual and textual learners. We design the Low-Rank Residual Attention (LoRRA) to guarantee high efficiency for learners. Our experimental results demonstrate that Wings outperforms equally-scaled MLLMs in both text-only and visual question-answering tasks. On a newly constructed Interleaved Image-Text (IIT) benchmark, Wings exhibits superior performance from text-only-rich to multimodal-rich question-answering tasks.
Parrot: Multilingual Visual Instruction Tuning
Jun 04, 2024



Abstract:The rapid development of Multimodal Large Language Models (MLLMs) like GPT-4V has marked a significant step towards artificial general intelligence. Existing methods mainly focus on aligning vision encoders with LLMs through supervised fine-tuning (SFT) to endow LLMs with multimodal abilities, making MLLMs' inherent ability to react to multiple languages progressively deteriorate as the training process evolves. We empirically find that the imbalanced SFT datasets, primarily composed of English-centric image-text pairs, lead to significantly reduced performance in non-English languages. This is due to the failure of aligning the vision encoder and LLM with multilingual tokens during the SFT process. In this paper, we introduce Parrot, a novel method that utilizes textual guidance to drive visual token alignment at the language level. Parrot makes the visual tokens condition on diverse language inputs and uses Mixture-of-Experts (MoE) to promote the alignment of multilingual tokens. Specifically, to enhance non-English visual tokens alignment, we compute the cross-attention using the initial visual features and textual embeddings, the result of which is then fed into the MoE router to select the most relevant experts. The selected experts subsequently convert the initial visual tokens into language-specific visual tokens. Moreover, considering the current lack of benchmarks for evaluating multilingual capabilities within the field, we collect and make available a Massive Multilingual Multimodal Benchmark which includes 6 languages, 15 categories, and 12,000 questions, named as MMMB. Our method not only demonstrates state-of-the-art performance on multilingual MMBench and MMMB, but also excels across a broad range of multimodal tasks. Both the source code and the training dataset of Parrot will be made publicly available.
Ovis: Structural Embedding Alignment for Multimodal Large Language Model
May 31, 2024



Abstract:Current Multimodal Large Language Models (MLLMs) typically integrate a pre-trained LLM with another pre-trained vision transformer through a connector, such as an MLP, endowing the LLM with visual capabilities. However, the misalignment between two embedding strategies in MLLMs -- the structural textual embeddings based on an embedding look-up table and the continuous embeddings generated directly by the vision encoder -- makes challenges for a more seamless fusion of visual and textual information. We propose Ovis, a novel MLLM architecture designed to structurally align visual and textual embeddings. Ovis integrates an additional learnable visual embedding table into the visual encoder's process. To capture rich visual semantics, each image patch indexes the visual embedding table multiple times, resulting in a final visual embedding that is a probabilistic combination of the indexed embeddings. This structural approach mirrors the method used for generating textual embeddings. Empirical evaluations on various multimodal benchmarks demonstrate that Ovis outperforms open-source MLLMs of similar parameter scales and even surpasses the proprietary model Qwen-VL-Plus overall. These results highlight the potential of Ovis' structured visual representation for advancing MLLM architectural design and promoting more effective multimodal learning. Both the source code and the training dataset of Ovis will be made publicly available.
Non-stationary Projection-free Online Learning with Dynamic and Adaptive Regret Guarantees
May 19, 2023



Abstract:Projection-free online learning has drawn increasing interest due to its efficiency in solving high-dimensional problems with complicated constraints. However, most existing projection-free online methods focus on minimizing the static regret, which unfortunately fails to capture the challenge of changing environments. In this paper, we investigate non-stationary projection-free online learning, and choose dynamic regret and adaptive regret to measure the performance. Specifically, we first provide a novel dynamic regret analysis for an existing projection-free method named $\text{BOGD}_\text{IP}$, and establish an $\mathcal{O}(T^{3/4}(1+P_T))$ dynamic regret bound, where $P_T$ denotes the path-length of the comparator sequence. Then, we improve the upper bound to $\mathcal{O}(T^{3/4}(1+P_T)^{1/4})$ by running multiple $\text{BOGD}_\text{IP}$ algorithms with different step sizes in parallel, and tracking the best one on the fly. Our results are the first general-case dynamic regret bounds for projection-free online learning, and can recover the existing $\mathcal{O}(T^{3/4})$ static regret by setting $P_T = 0$. Furthermore, we propose a projection-free method to attain an $\tilde{\mathcal{O}}(\tau^{3/4})$ adaptive regret bound for any interval with length $\tau$, which nearly matches the static regret over that interval. The essential idea is to maintain a set of $\text{BOGD}_\text{IP}$ algorithms dynamically, and combine them by a meta algorithm. Moreover, we demonstrate that it is also equipped with an $\mathcal{O}(T^{3/4}(1+P_T)^{1/4})$ dynamic regret bound. Finally, empirical studies verify our theoretical findings.
Revisiting Smoothed Online Learning
Feb 13, 2021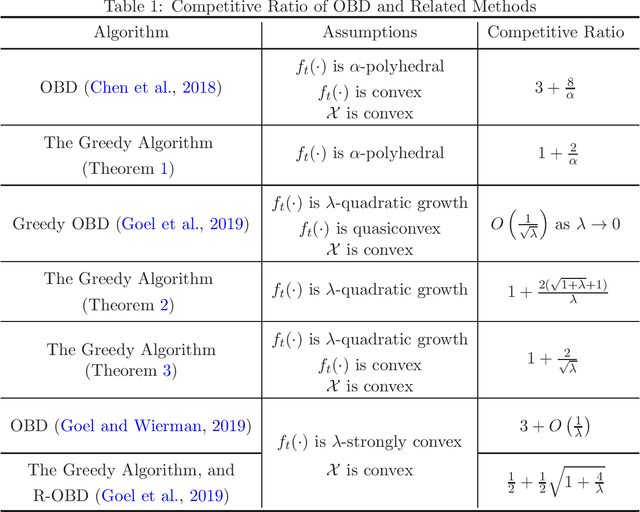

Abstract:In this paper, we revisit the problem of smoothed online learning, in which the online learner suffers both a hitting cost and a switching cost, and target two performance metrics: competitive ratio and dynamic regret with switching cost. To bound the competitive ratio, we assume the hitting cost is known to the learner in each round, and investigate the greedy algorithm which simply minimizes the weighted sum of the hitting cost and the switching cost. Our theoretical analysis shows that the greedy algorithm, although straightforward, is $1+ \frac{2}{\alpha}$-competitive for $\alpha$-polyhedral functions, $1+O(\frac{1}{\lambda})$-competitive for $\lambda$-quadratic growth functions, and $1 + \frac{2}{\sqrt{\lambda}}$-competitive for convex and $\lambda$-quadratic growth functions. To bound the dynamic regret with switching cost, we follow the standard setting of online convex optimization, in which the hitting cost is convex but hidden from the learner before making predictions. We modify Ader, an existing algorithm designed for dynamic regret, slightly to take into account the switching cost when measuring the performance. The proposed algorithm, named as Smoothed Ader, attains an optimal $O(\sqrt{T(1+P_T)})$ bound for dynamic regret with switching cost, where $P_T$ is the path-length of the comparator sequence. Furthermore, if the hitting cost is accessible in the beginning of each round, we obtain a similar guarantee without the bounded gradient condition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge