Improved Approximate Regret for Decentralized Online Continuous Submodular Maximization via Reductions

To expand the applicability of decentralized online learning, previous studies have proposed several algorithms for decentralized online continuous submodular maximization (D-OCSM) -- a non-convex/non-concave setting with continuous DR-submodular reward functions. However, there exist large gaps between their approximate regret bounds and the regret bounds achieved in the convex setting. Moreover, if focusing on projection-free algorithms, which can efficiently handle complex decision sets, they cannot even recover the approximate regret bounds achieved in the centralized setting. In this paper, we first demonstrate that for D-OCSM over general convex decision sets, these two issues can be addressed simultaneously. Furthermore, for D-OCSM over downward-closed decision sets, we show that the second issue can be addressed while significantly alleviating the first issue. Our key techniques are two reductions from D-OCSM to decentralized online convex optimization (D-OCO), which can exploit D-OCO algorithms to improve the approximate regret of D-OCSM in these two cases, respectively.

Sign-Based Optimizers Are Effective Under Heavy-Tailed Noise

While adaptive gradient methods are the workhorse of modern machine learning, sign-based optimization algorithms such as Lion and Muon have recently demonstrated superior empirical performance over AdamW in training large language models (LLM). However, a theoretical understanding of why sign-based updates outperform variance-adapted methods remains elusive. In this paper, we aim to bridge the gap between theory and practice through the lens of heavy-tailed gradient noise, a phenomenon frequently observed in language modeling tasks. Theoretically, we introduce a novel generalized heavy-tailed noise condition that captures the behavior of LLMs more accurately than standard finite variance assumptions. Under this noise model, we establish sharp convergence rates of SignSGD and Lion for generalized smooth function classes, matching or surpassing previous best-known bounds. Furthermore, we extend our analysis to Muon and Muonlight, providing what is, to our knowledge, the first rigorous analysis of matrix optimization under heavy-tailed stochasticity. These results offer a strong theoretical justification for the empirical superiority of sign-based optimizers, showcasing that they are naturally suited to handle the noisy gradients associated with heavy tails. Empirically, LLM pretraining experiments validate our theoretical insights and confirm that our proposed noise models are well-aligned with practice.

KeepLoRA: Continual Learning with Residual Gradient Adaptation

Continual learning for pre-trained vision-language models requires balancing three competing objectives: retaining pre-trained knowledge, preserving knowledge from a sequence of learned tasks, and maintaining the plasticity to acquire new knowledge. This paper presents a simple but effective approach called KeepLoRA to effectively balance these objectives. We first analyze the knowledge retention mechanism within the model parameter space and find that general knowledge is mainly encoded in the principal subspace, while task-specific knowledge is encoded in the residual subspace. Motivated by this finding, KeepLoRA learns new tasks by restricting LoRA parameter updates in the residual subspace to prevent interfering with previously learned capabilities. Specifically, we infuse knowledge for a new task by projecting its gradient onto a subspace orthogonal to both the principal subspace of pre-trained model and the dominant directions of previous task features. Our theoretical and empirical analyses confirm that KeepLoRA balances the three objectives and achieves state-of-the-art performance. The implementation code is available at https://github.com/MaolinLuo/KeepLoRA.

Deep But Reliable: Advancing Multi-turn Reasoning for Thinking with Images

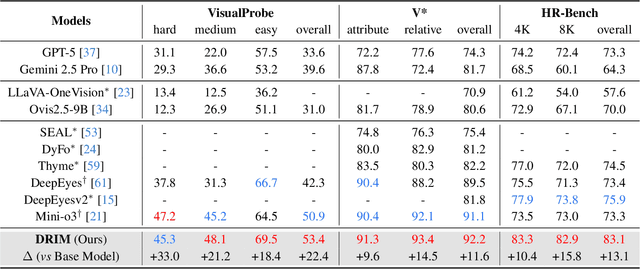
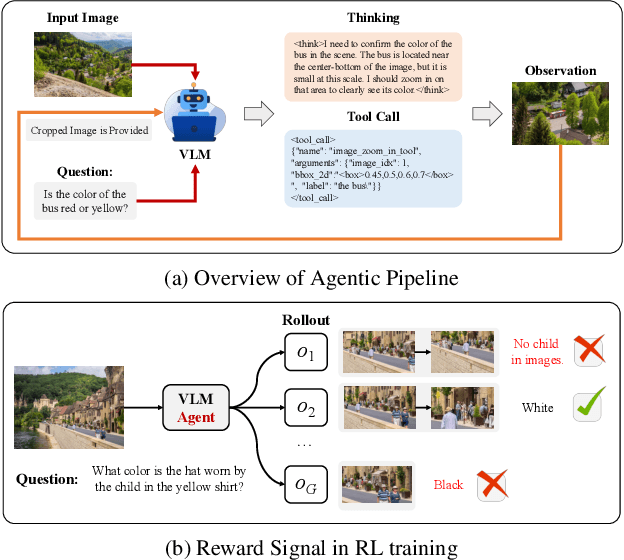
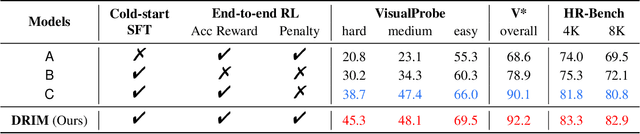
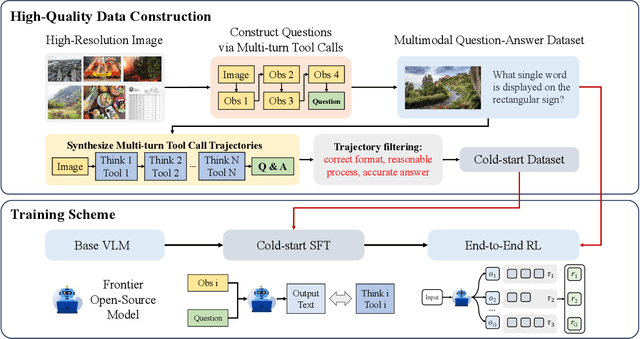
Recent advances in large Vision-Language Models (VLMs) have exhibited strong reasoning capabilities on complex visual tasks by thinking with images in their Chain-of-Thought (CoT), which is achieved by actively invoking tools to analyze visual inputs rather than merely perceiving them. However, existing models often struggle to reflect on and correct themselves when attempting incorrect reasoning trajectories. To address this limitation, we propose DRIM, a model that enables deep but reliable multi-turn reasoning when thinking with images in its multimodal CoT. Our pipeline comprises three stages: data construction, cold-start SFT and RL. Based on a high-resolution image dataset, we construct high-difficulty and verifiable visual question-answer pairs, where solving each task requires multi-turn tool calls to reach the correct answer. In the SFT stage, we collect tool trajectories as cold-start data, guiding a multi-turn reasoning pattern. In the RL stage, we introduce redundancy-penalized policy optimization, which incentivizes the model to develop a self-reflective reasoning pattern. The basic idea is to impose judgment on reasoning trajectories and penalize those that produce incorrect answers without sufficient multi-scale exploration. Extensive experiments demonstrate that DRIM achieves superior performance on visual understanding benchmarks.

Beyond the Lower Bound: Bridging Regret Minimization and Best Arm Identification in Lexicographic Bandits

In multi-objective decision-making with hierarchical preferences, lexicographic bandits provide a natural framework for optimizing multiple objectives in a prioritized order. In this setting, a learner repeatedly selects arms and observes reward vectors, aiming to maximize the reward for the highest-priority objective, then the next, and so on. While previous studies have primarily focused on regret minimization, this work bridges the gap between \textit{regret minimization} and \textit{best arm identification} under lexicographic preferences. We propose two elimination-based algorithms to address this joint objective. The first algorithm eliminates suboptimal arms sequentially, layer by layer, in accordance with the objective priorities, and achieves sample complexity and regret bounds comparable to those of the best single-objective algorithms. The second algorithm simultaneously leverages reward information from all objectives in each round, effectively exploiting cross-objective dependencies. Remarkably, it outperforms the known lower bound for the single-objective bandit problem, highlighting the benefit of cross-objective information sharing in the multi-objective setting. Empirical results further validate their superior performance over baselines.

Dataset Ownership Verification for Pre-trained Masked Models

High-quality open-source datasets have emerged as a pivotal catalyst driving the swift advancement of deep learning, while facing the looming threat of potential exploitation. Protecting these datasets is of paramount importance for the interests of their owners. The verification of dataset ownership has evolved into a crucial approach in this domain; however, existing verification techniques are predominantly tailored to supervised models and contrastive pre-trained models, rendering them ill-suited for direct application to the increasingly prevalent masked models. In this work, we introduce the inaugural methodology addressing this critical, yet unresolved challenge, termed Dataset Ownership Verification for Masked Modeling (DOV4MM). The central objective is to ascertain whether a suspicious black-box model has been pre-trained on a particular unlabeled dataset, thereby assisting dataset owners in safeguarding their rights. DOV4MM is grounded in our empirical observation that when a model is pre-trained on the target dataset, the difficulty of reconstructing masked information within the embedding space exhibits a marked contrast to models not pre-trained on that dataset. We validated the efficacy of DOV4MM through ten masked image models on ImageNet-1K and four masked language models on WikiText-103. The results demonstrate that DOV4MM rejects the null hypothesis, with a $p$-value considerably below 0.05, surpassing all prior approaches. Code is available at https://github.com/xieyc99/DOV4MM.

Continuous Subspace Optimization for Continual Learning

Continual learning aims to learn multiple tasks sequentially while preserving prior knowledge, but faces the challenge of catastrophic forgetting when acquiring new knowledge. Recently, approaches leveraging pre-trained models have gained increasing popularity to mitigate this issue, due to the strong generalization ability of foundation models. To adjust pre-trained models for new tasks, existing methods usually employ low-rank adaptation, which restricts parameter updates to a fixed low-rank subspace. However, constraining the optimization space inherently compromises the model's learning capacity, resulting in inferior performance. To address the limitation, we propose Continuous Subspace Optimization for Continual Learning (CoSO) to fine-tune the model in a series of subspaces rather than a single one. These sequential subspaces are dynamically determined through the singular value decomposition of gradients. CoSO updates the model by projecting gradients into these subspaces, ensuring memory-efficient optimization. To mitigate forgetting, the optimization subspaces of each task are set to be orthogonal to the historical task subspace. During task learning, CoSO maintains a task-specific component that captures the critical update directions associated with the current task. Upon completing a task, this component is used to update the historical task subspace, laying the groundwork for subsequent learning. Extensive experiments on multiple datasets demonstrate that CoSO significantly outperforms state-of-the-art methods, especially in challenging scenarios with long task sequences.

Quantizing Diffusion Models from a Sampling-Aware Perspective

Diffusion models have recently emerged as the dominant approach in visual generation tasks. However, the lengthy denoising chains and the computationally intensive noise estimation networks hinder their applicability in low-latency and resource-limited environments. Previous research has endeavored to address these limitations in a decoupled manner, utilizing either advanced samplers or efficient model quantization techniques. In this study, we uncover that quantization-induced noise disrupts directional estimation at each sampling step, further distorting the precise directional estimations of higher-order samplers when solving the sampling equations through discretized numerical methods, thereby altering the optimal sampling trajectory. To attain dual acceleration with high fidelity, we propose a sampling-aware quantization strategy, wherein a Mixed-Order Trajectory Alignment technique is devised to impose a more stringent constraint on the error bounds at each sampling step, facilitating a more linear probability flow. Extensive experiments on sparse-step fast sampling across multiple datasets demonstrate that our approach preserves the rapid convergence characteristics of high-speed samplers while maintaining superior generation quality. Code will be made publicly available soon.

Revisiting Multi-Agent Asynchronous Online Optimization with Delays: the Strongly Convex Case

We revisit multi-agent asynchronous online optimization with delays, where only one of the agents becomes active for making the decision at each round, and the corresponding feedback is received by all the agents after unknown delays. Although previous studies have established an $O(\sqrt{dT})$ regret bound for this problem, they assume that the maximum delay $d$ is knowable or the arrival order of feedback satisfies a special property, which may not hold in practice. In this paper, we surprisingly find that when the loss functions are strongly convex, these assumptions can be eliminated, and the existing regret bound can be significantly improved to $O(d\log T)$ meanwhile. Specifically, to exploit the strong convexity of functions, we first propose a delayed variant of the classical follow-the-leader algorithm, namely FTDL, which is very simple but requires the full information of functions as feedback. Moreover, to handle the more general case with only the gradient feedback, we develop an approximate variant of FTDL by combining it with surrogate loss functions. Experimental results show that the approximate FTDL outperforms the existing algorithm in the strongly convex case.

Mirror Descent Under Generalized Smoothness

Smoothness is crucial for attaining fast rates in first-order optimization. However, many optimization problems in modern machine learning involve non-smooth objectives. Recent studies relax the smoothness assumption by allowing the Lipschitz constant of the gradient to grow with respect to the gradient norm, which accommodates a broad range of objectives in practice. Despite this progress, existing generalizations of smoothness are restricted to Euclidean geometry with $\ell_2$-norm and only have theoretical guarantees for optimization in the Euclidean space. In this paper, we address this limitation by introducing a new $\ell*$-smoothness concept that measures the norm of Hessian in terms of a general norm and its dual, and establish convergence for mirror-descent-type algorithms, matching the rates under the classic smoothness. Notably, we propose a generalized self-bounding property that facilitates bounding the gradients via controlling suboptimality gaps, serving as a principal component for convergence analysis. Beyond deterministic optimization, we establish an anytime convergence for stochastic mirror descent based on a new bounded noise condition that encompasses the widely adopted bounded or affine noise assumptions.