SSGCNet: A Sparse Spectra Graph Convolutional Network for Epileptic EEG Signal Classification

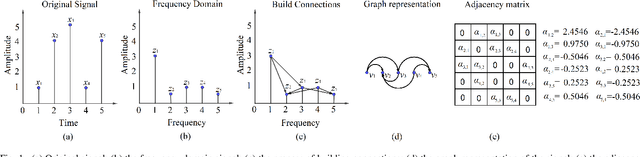
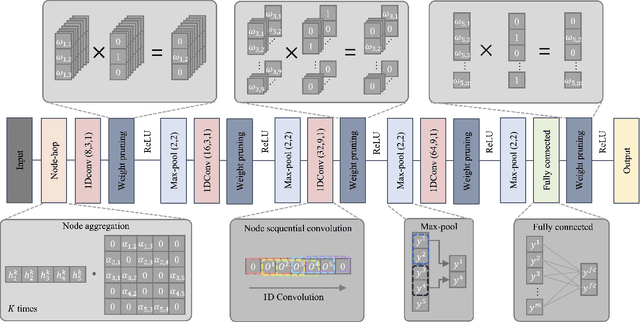
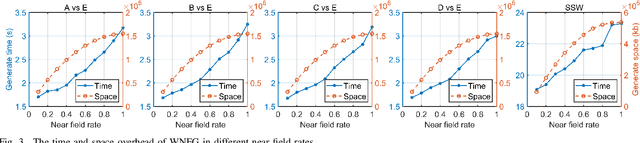
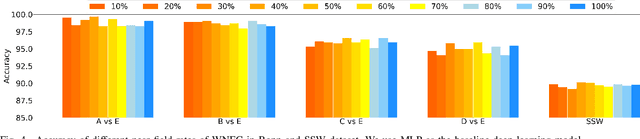
In this article, we propose a sparse spectra graph convolutional network (SSGCNet) for solving Epileptic EEG signal classification problems. The aim is to achieve a lightweight deep learning model without losing model classification accuracy. We propose a weighted neighborhood field graph (WNFG) to represent EEG signals, which reduces the redundant edges between graph nodes. WNFG has lower time complexity and memory usage than the conventional solutions. Using the graph representation, the sequential graph convolutional network is based on a combination of sparse weight pruning technique and the alternating direction method of multipliers (ADMM). Our approach can reduce computation complexity without effect on classification accuracy. We also present convergence results for the proposed approach. The performance of the approach is illustrated in public and clinical-real datasets. Compared with the existing literature, our WNFG of EEG signals achieves up to 10 times of redundant edge reduction, and our approach achieves up to 97 times of model pruning without loss of classification accuracy.

Reinforcement Learned Distributed Multi-Robot Navigation with Reciprocal Velocity Obstacle Shaped Rewards

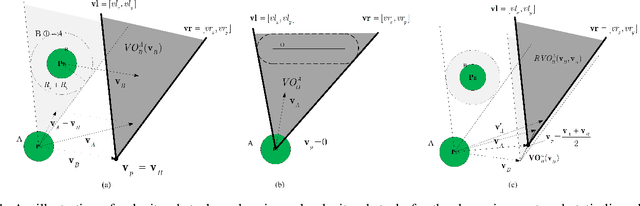
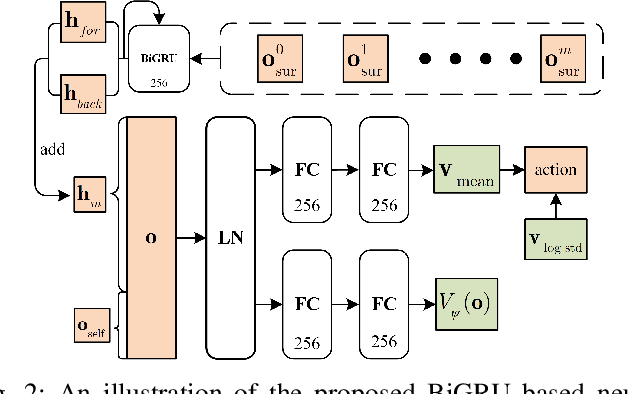
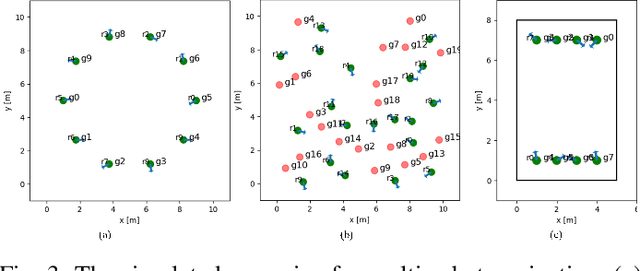
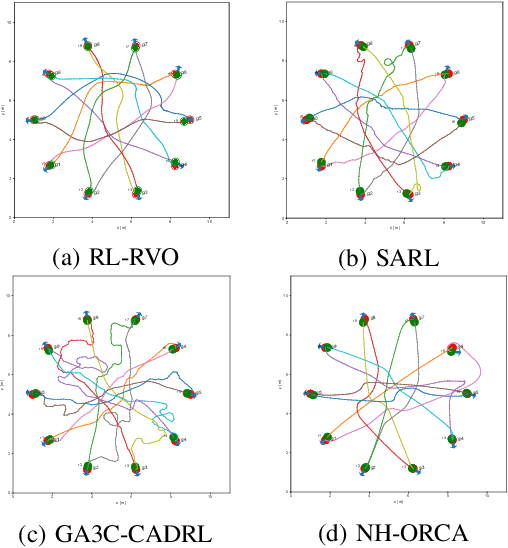
The challenges to solving the collision avoidance problem lie in adaptively choosing optimal robot velocities in complex scenarios full of interactive obstacles. In this paper, we propose a distributed approach for multi-robot navigation which combines the concept of reciprocal velocity obstacle (RVO) and the scheme of deep reinforcement learning (DRL) to solve the reciprocal collision avoidance problem under limited information. The novelty of this work is threefold: (1) using a set of sequential VO and RVO vectors to represent the interactive environmental states of static and dynamic obstacles, respectively; (2) developing a bidirectional recurrent module based neural network, which maps the states of a varying number of surrounding obstacles to the actions directly; (3) developing a RVO area and expected collision time based reward function to encourage reciprocal collision avoidance behaviors and trade off between collision risk and travel time. The proposed policy is trained through simulated scenarios and updated by the actor-critic based DRL algorithm. We validate the policy in complex environments with various numbers of differential drive robots and obstacles. The experiment results demonstrate that our approach outperforms the state-of-art methods and other learning based approaches in terms of the success rate, travel time, and average speed. Source code of this approach is available at https://github.com/hanruihua/rl_rvo_nav.

Adaptive Environment Modeling Based Reinforcement Learning for Collision Avoidance in Complex Scenes

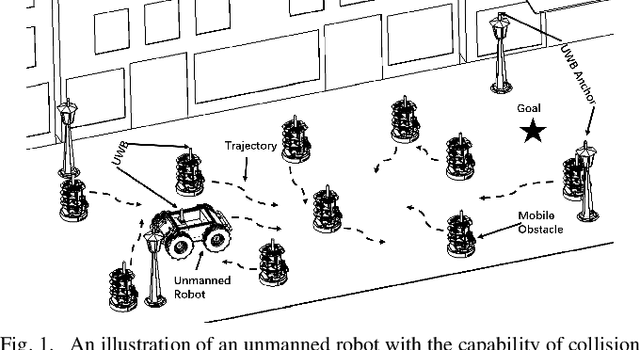
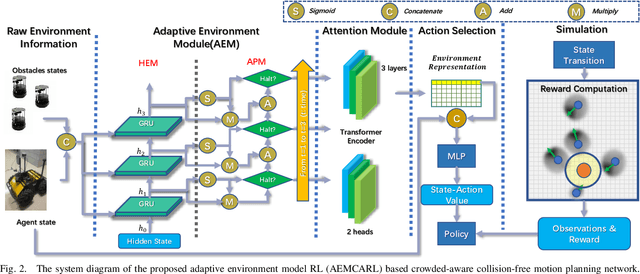
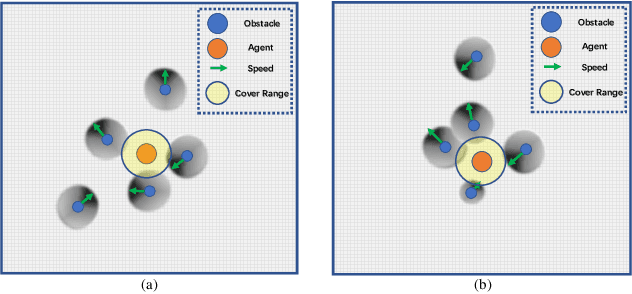
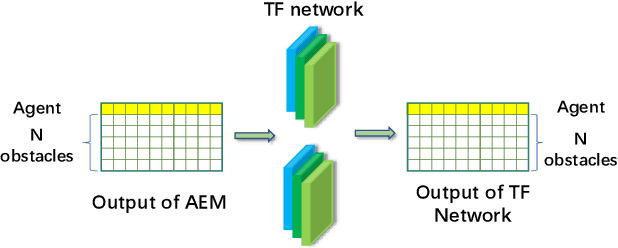
The major challenges of collision avoidance for robot navigation in crowded scenes lie in accurate environment modeling, fast perceptions, and trustworthy motion planning policies. This paper presents a novel adaptive environment model based collision avoidance reinforcement learning (i.e., AEMCARL) framework for an unmanned robot to achieve collision-free motions in challenging navigation scenarios. The novelty of this work is threefold: (1) developing a hierarchical network of gated-recurrent-unit (GRU) for environment modeling; (2) developing an adaptive perception mechanism with an attention module; (3) developing an adaptive reward function for the reinforcement learning (RL) framework to jointly train the environment model, perception function and motion planning policy. The proposed method is tested with the Gym-Gazebo simulator and a group of robots (Husky and Turtlebot) under various crowded scenes. Both simulation and experimental results have demonstrated the superior performance of the proposed method over baseline methods.

Absolute Zero-Shot Learning

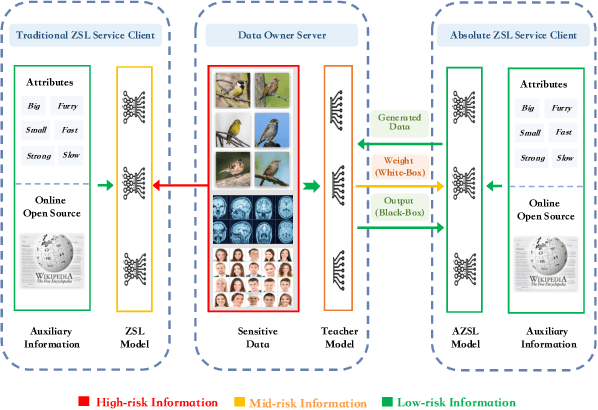
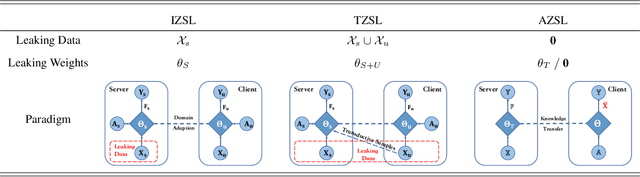
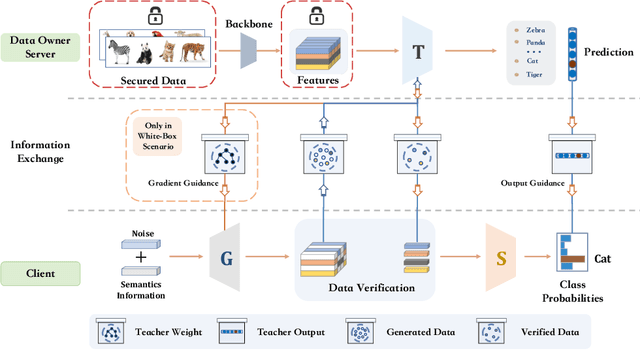
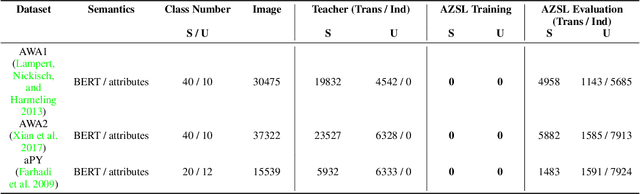
Considering the increasing concerns about data copyright and privacy issues, we present a novel Absolute Zero-Shot Learning (AZSL) paradigm, i.e., training a classifier with zero real data. The key innovation is to involve a teacher model as the data safeguard to guide the AZSL model training without data leaking. The AZSL model consists of a generator and student network, which can achieve date-free knowledge transfer while maintaining the performance of the teacher network. We investigate `black-box' and `white-box' scenarios in AZSL task as different levels of model security. Besides, we also provide discussion of teacher model in both inductive and transductive settings. Despite embarrassingly simple implementations and data-missing disadvantages, our AZSL framework can retain state-of-the-art ZSL and GZSL performance under the `white-box' scenario. Extensive qualitative and quantitative analysis also demonstrates promising results when deploying the model under `black-box' scenario.

Phase-SLAM: Phase Based Simultaneous Localization and Mapping for Mobile Structured Light Illumination Systems

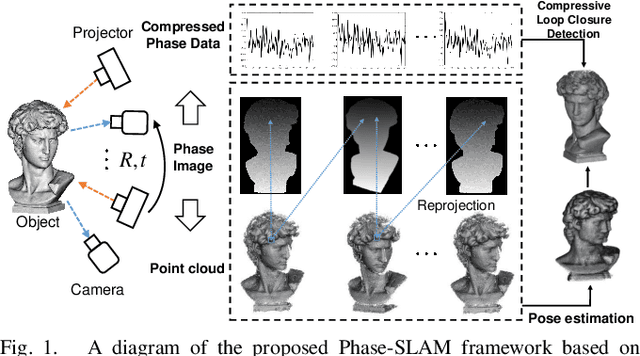
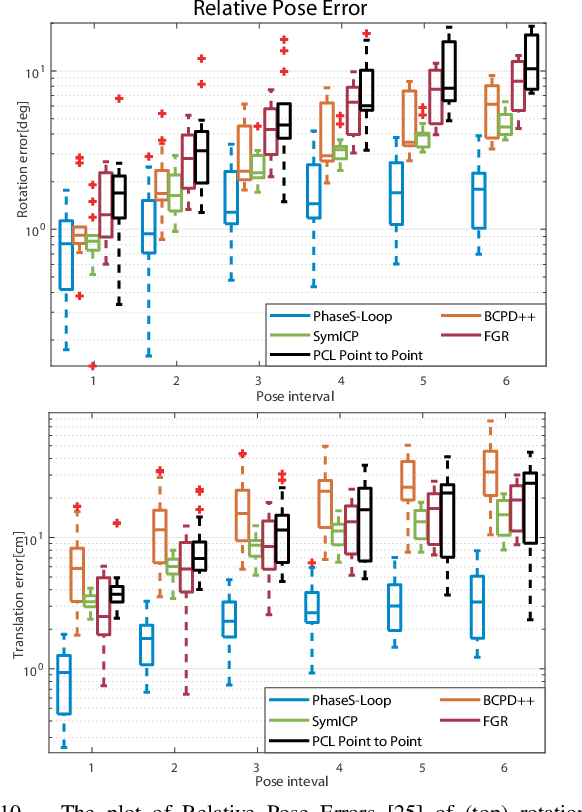
Structured Light Illumination (SLI) systems have been used for reliable indoor dense 3D scanning via phase triangulation. However, mobile SLI systems for 360 degree 3D reconstruction demand 3D point cloud registration, involving high computational complexity. In this paper, we propose a phase based Simultaneous Localization and Mapping (Phase-SLAM) framework for fast and accurate SLI sensor pose estimation and 3D object reconstruction. The novelty of this work is threefold: (1) developing a reprojection model from 3D points to 2D phase data towards phase registration with low computational complexity; (2) developing a local optimizer to achieve SLI sensor pose estimation (odometry) using the derived Jacobian matrix for the 6 DoF variables; (3) developing a compressive phase comparison method to achieve high-efficiency loop closure detection. The whole Phase-SLAM pipeline is then exploited using existing global pose graph optimization techniques. We build datasets from both the unreal simulation platform and a robotic arm based SLI system in real-world to verify the proposed approach. The experiment results demonstrate that the proposed Phase-SLAM outperforms other state-of-the-art methods in terms of the efficiency and accuracy of pose estimation and 3D reconstruction. The open-source code is available at https://github.com/ZHENGXi-git/Phase-SLAM.

Sinkhorn Distributionally Robust Optimization

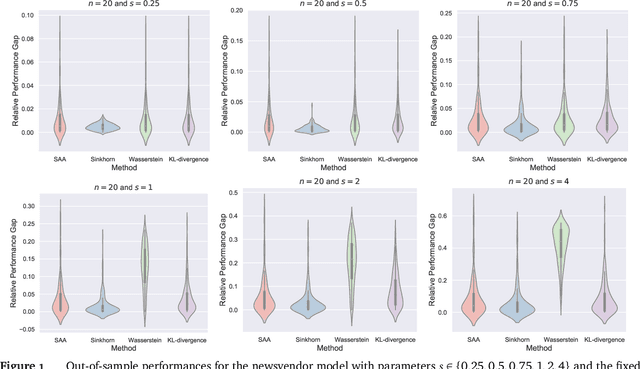
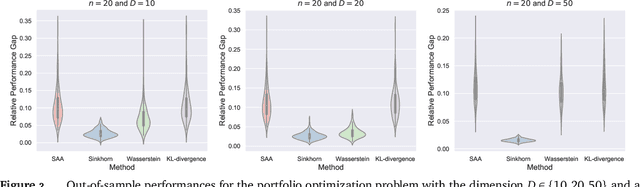
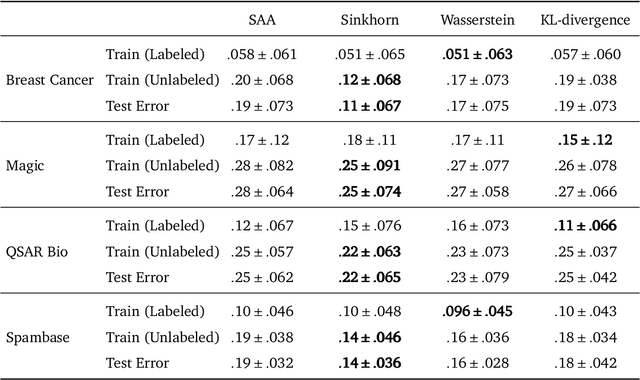
We study distributionally robust optimization with Sinkorn distance -- a variant of Wasserstein distance based on entropic regularization. We derive convex programming dual reformulations when the nominal distribution is an empirical distribution and a general distribution, respectively. Compared with Wasserstein DRO, it is computationally tractable for a larger class of loss functions, and its worst-case distribution is more reasonable. To solve the dual reformulation, we propose an efficient batch gradient descent with a bisection search algorithm. Finally, we provide various numerical examples using both synthetic and real data to demonstrate its competitive performance.

Hierarchical Non-Stationary Temporal Gaussian Processes With $L^1$-Regularization

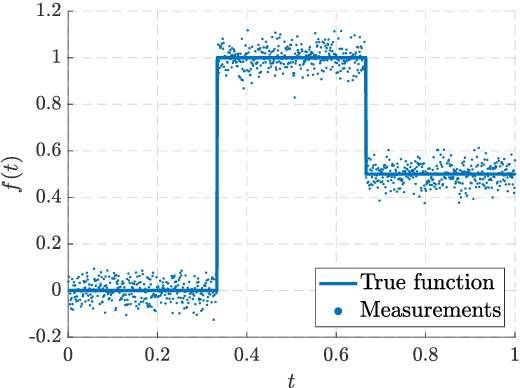
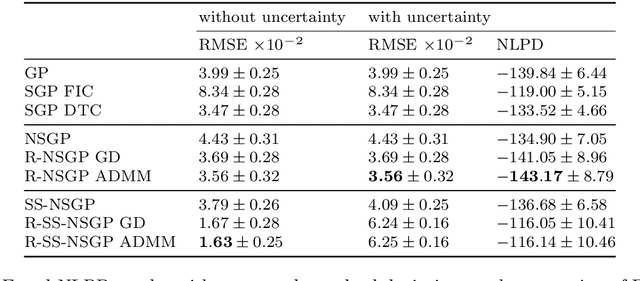
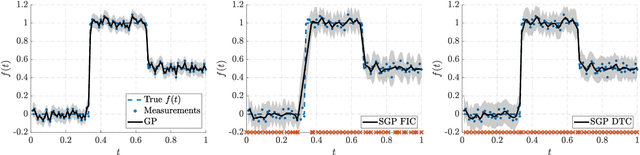
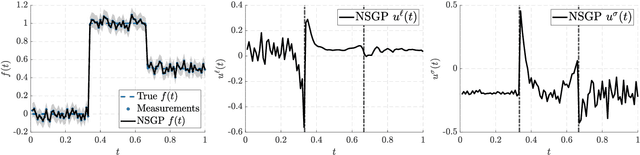
This paper is concerned with regularized extensions of hierarchical non-stationary temporal Gaussian processes (NSGPs) in which the parameters (e.g., length-scale) are modeled as GPs. In particular, we consider two commonly used NSGP constructions which are based on explicitly constructed non-stationary covariance functions and stochastic differential equations, respectively. We extend these NSGPs by including $L^1$-regularization on the processes in order to induce sparseness. To solve the resulting regularized NSGP (R-NSGP) regression problem we develop a method based on the alternating direction method of multipliers (ADMM) and we also analyze its convergence properties theoretically. We also evaluate the performance of the proposed methods in simulated and real-world datasets.

Learning While Dissipating Information: Understanding the Generalization Capability of SGLD

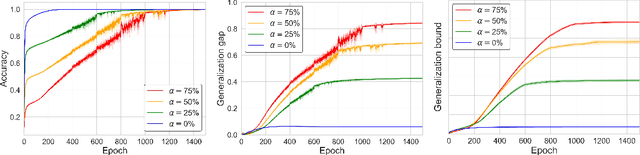
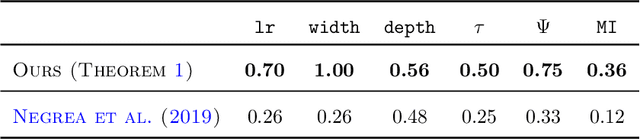
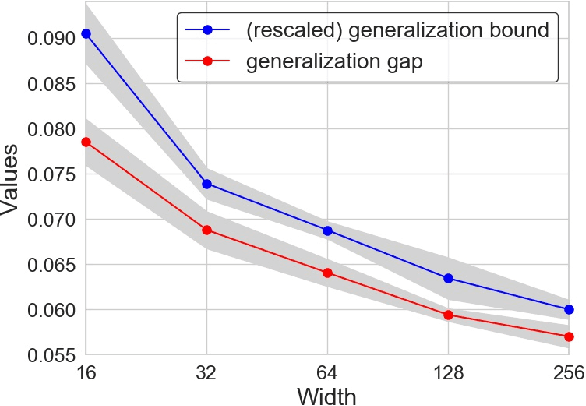
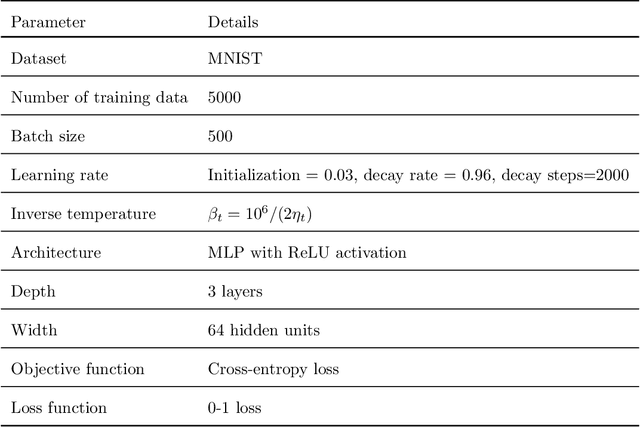
Understanding the generalization capability of learning algorithms is at the heart of statistical learning theory. In this paper, we investigate the generalization gap of stochastic gradient Langevin dynamics (SGLD), a widely used optimizer for training deep neural networks (DNNs). We derive an algorithm-dependent generalization bound by analyzing SGLD through an information-theoretic lens. Our analysis reveals an intricate trade-off between learning and information dissipation: SGLD learns from data by updating parameters at each iteration while dissipating information from early training stages. Our bound also involves the variance of gradients which captures a particular kind of "sharpness" of the loss landscape. The main proof techniques in this paper rely on strong data processing inequalities -- a fundamental concept in information theory -- and Otto-Villani's HWI inequality. Finally, we demonstrate our bound through numerical experiments, showing that it can predict the behavior of the true generalization gap.

Generalize Ultrasound Image Segmentation via Instant and Plug & Play Style Transfer

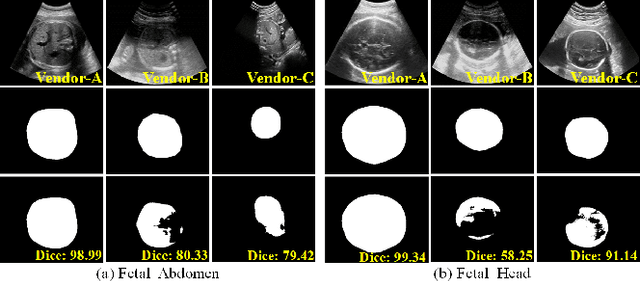
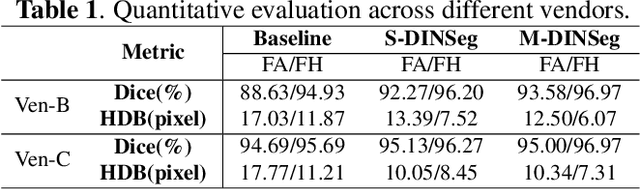
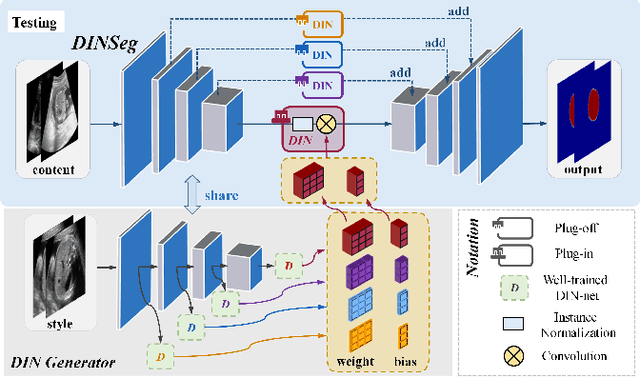
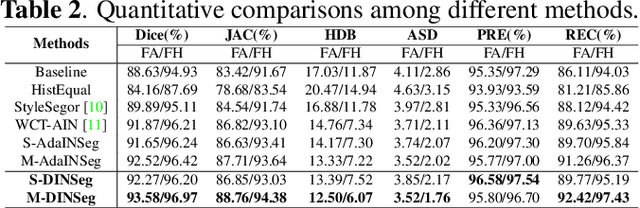
Deep segmentation models that generalize to images with unknown appearance are important for real-world medical image analysis. Retraining models leads to high latency and complex pipelines, which are impractical in clinical settings. The situation becomes more severe for ultrasound image analysis because of their large appearance shifts. In this paper, we propose a novel method for robust segmentation under unknown appearance shifts. Our contribution is three-fold. First, we advance a one-stage plug-and-play solution by embedding hierarchical style transfer units into a segmentation architecture. Our solution can remove appearance shifts and perform segmentation simultaneously. Second, we adopt Dynamic Instance Normalization to conduct precise and dynamic style transfer in a learnable manner, rather than previously fixed style normalization. Third, our solution is fast and lightweight for routine clinical adoption. Given 400*400 image input, our solution only needs an additional 0.2ms and 1.92M FLOPs to handle appearance shifts compared to the baseline pipeline. Extensive experiments are conducted on a large dataset from three vendors demonstrate our proposed method enhances the robustness of deep segmentation models.

Reliable Off-policy Evaluation for Reinforcement Learning

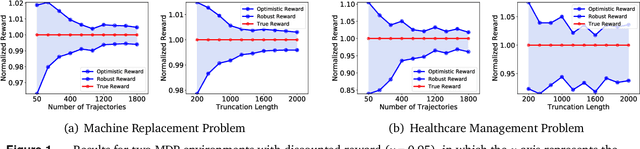
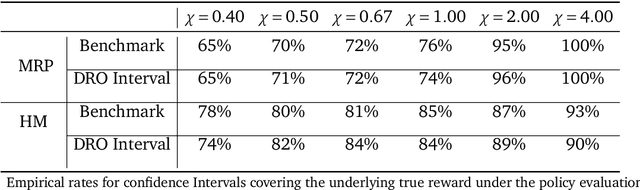
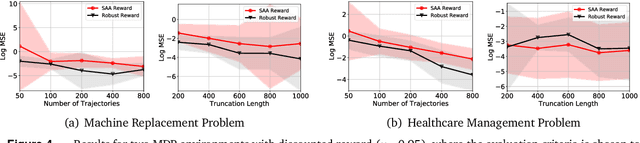
In a sequential decision-making problem, off-policy evaluation (OPE) estimates the expected cumulative reward of a target policy using logged transition data generated from a different behavior policy, without execution of the target policy. Reinforcement learning in high-stake environments, such as healthcare and education, is often limited to off-policy settings due to safety or ethical concerns, or inability of exploration. Hence it is imperative to quantify the uncertainty of the off-policy estimate before deployment of the target policy. In this paper, we propose a novel framework that provides robust and optimistic cumulative reward estimates with statistical guarantees and develop non-asymptotic as well as asymptotic confidence intervals for OPE, leveraging methodologies from distributionally robust optimization. Our theoretical results are also supported by empirical analysis.