Detecting Post-generation Edits to Watermarked LLM Outputs via Combinatorial Watermarking

Watermarking has become a key technique for proprietary language models, enabling the distinction between AI-generated and human-written text. However, in many real-world scenarios, LLM-generated content may undergo post-generation edits, such as human revisions or even spoofing attacks, making it critical to detect and localize such modifications. In this work, we introduce a new task: detecting post-generation edits locally made to watermarked LLM outputs. To this end, we propose a combinatorial pattern-based watermarking framework, which partitions the vocabulary into disjoint subsets and embeds the watermark by enforcing a deterministic combinatorial pattern over these subsets during generation. We accompany the combinatorial watermark with a global statistic that can be used to detect the watermark. Furthermore, we design lightweight local statistics to flag and localize potential edits. We introduce two task-specific evaluation metrics, Type-I error rate and detection accuracy, and evaluate our method on open-source LLMs across a variety of editing scenarios, demonstrating strong empirical performance in edit localization.

Error Analysis of Discrete Flow with Generator Matching

Discrete flow models offer a powerful framework for learning distributions over discrete state spaces and have demonstrated superior performance compared to the discrete diffusion model. However, their convergence properties and error analysis remain largely unexplored. In this work, we develop a unified framework grounded in stochastic calculus theory to systematically investigate the theoretical properties of discrete flow. Specifically, we derive the KL divergence of two path measures regarding two continuous-time Markov chains (CTMCs) with different transition rates by developing a novel Girsanov-type theorem, and provide a comprehensive analysis that encompasses the error arising from transition rate estimation and early stopping, where the first type of error has rarely been analyzed by existing works. Unlike discrete diffusion models, discrete flow incurs no truncation error caused by truncating the time horizon in the noising process. Building on generator matching and uniformization, we establish non-asymptotic error bounds for distribution estimation. Our results provide the first error analysis for discrete flow models.

Discrete Guidance Matching: Exact Guidance for Discrete Flow Matching

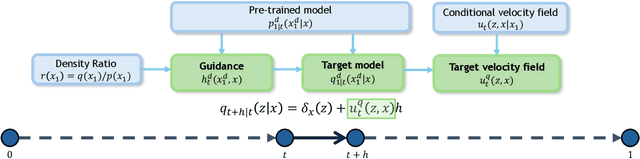
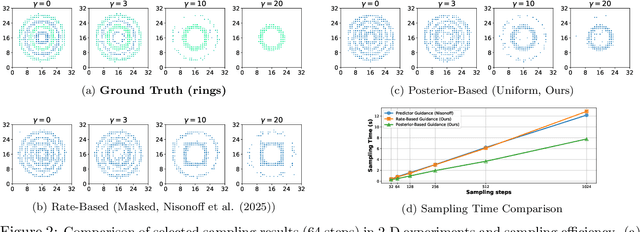
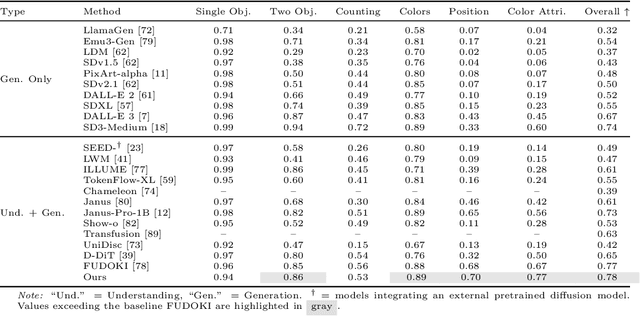
Guidance provides a simple and effective framework for posterior sampling by steering the generation process towards the desired distribution. When modeling discrete data, existing approaches mostly focus on guidance with the first-order Taylor approximation to improve the sampling efficiency. However, such an approximation is inappropriate in discrete state spaces since the approximation error could be large. A novel guidance framework for discrete data is proposed to address this problem: We derive the exact transition rate for the desired distribution given a learned discrete flow matching model, leading to guidance that only requires a single forward pass in each sampling step, significantly improving efficiency. This unified novel framework is general enough, encompassing existing guidance methods as special cases, and it can also be seamlessly applied to the masked diffusion model. We demonstrate the effectiveness of our proposed guidance on energy-guided simulations and preference alignment on text-to-image generation and multimodal understanding tasks. The code is available through https://github.com/WanZhengyan/Discrete-Guidance-Matching/tree/main.

Recurrent Neural Goodness-of-Fit Test for Time Series

Time series data are crucial across diverse domains such as finance and healthcare, where accurate forecasting and decision-making rely on advanced modeling techniques. While generative models have shown great promise in capturing the intricate dynamics inherent in time series, evaluating their performance remains a major challenge. Traditional evaluation metrics fall short due to the temporal dependencies and potential high dimensionality of the features. In this paper, we propose the REcurrent NeurAL (RENAL) Goodness-of-Fit test, a novel and statistically rigorous framework for evaluating generative time series models. By leveraging recurrent neural networks, we transform the time series into conditionally independent data pairs, enabling the application of a chi-square-based goodness-of-fit test to the temporal dependencies within the data. This approach offers a robust, theoretically grounded solution for assessing the quality of generative models, particularly in settings with limited time sequences. We demonstrate the efficacy of our method across both synthetic and real-world datasets, outperforming existing methods in terms of reliability and accuracy. Our method fills a critical gap in the evaluation of time series generative models, offering a tool that is both practical and adaptable to high-stakes applications.

Transfer Learning for Diffusion Models

Diffusion models, a specific type of generative model, have achieved unprecedented performance in recent years and consistently produce high-quality synthetic samples. A critical prerequisite for their notable success lies in the presence of a substantial number of training samples, which can be impractical in real-world applications due to high collection costs or associated risks. Consequently, various finetuning and regularization approaches have been proposed to transfer knowledge from existing pre-trained models to specific target domains with limited data. This paper introduces the Transfer Guided Diffusion Process (TGDP), a novel approach distinct from conventional finetuning and regularization methods. We prove that the optimal diffusion model for the target domain integrates pre-trained diffusion models on the source domain with additional guidance from a domain classifier. We further extend TGDP to a conditional version for modeling the joint distribution of data and its corresponding labels, together with two additional regularization terms to enhance the model performance. We validate the effectiveness of TGDP on Gaussian mixture simulations and on real electrocardiogram (ECG) datasets.

$e^{\text{RPCA}}$: Robust Principal Component Analysis for Exponential Family Distributions

Robust Principal Component Analysis (RPCA) is a widely used method for recovering low-rank structure from data matrices corrupted by significant and sparse outliers. These corruptions may arise from occlusions, malicious tampering, or other causes for anomalies, and the joint identification of such corruptions with low-rank background is critical for process monitoring and diagnosis. However, existing RPCA methods and their extensions largely do not account for the underlying probabilistic distribution for the data matrices, which in many applications are known and can be highly non-Gaussian. We thus propose a new method called Robust Principal Component Analysis for Exponential Family distributions ($e^{\text{RPCA}}$), which can perform the desired decomposition into low-rank and sparse matrices when such a distribution falls within the exponential family. We present a novel alternating direction method of multiplier optimization algorithm for efficient $e^{\text{RPCA}}$ decomposition. The effectiveness of $e^{\text{RPCA}}$ is then demonstrated in two applications: the first for steel sheet defect detection, and the second for crime activity monitoring in the Atlanta metropolitan area.

MissDiff: Training Diffusion Models on Tabular Data with Missing Values

The diffusion model has shown remarkable performance in modeling data distributions and synthesizing data. However, the vanilla diffusion model requires complete or fully observed data for training. Incomplete data is a common issue in various real-world applications, including healthcare and finance, particularly when dealing with tabular datasets. This work presents a unified and principled diffusion-based framework for learning from data with missing values under various missing mechanisms. We first observe that the widely adopted "impute-then-generate" pipeline may lead to a biased learning objective. Then we propose to mask the regression loss of Denoising Score Matching in the training phase. We prove the proposed method is consistent in learning the score of data distributions, and the proposed training objective serves as an upper bound for the negative likelihood in certain cases. The proposed framework is evaluated on multiple tabular datasets using realistic and efficacious metrics and is demonstrated to outperform state-of-the-art diffusion model on tabular data with "impute-then-generate" pipeline by a large margin.

Neural Differential Recurrent Neural Network with Adaptive Time Steps

The neural Ordinary Differential Equation (ODE) model has shown success in learning complex continuous-time processes from observations on discrete time stamps. In this work, we consider the modeling and forecasting of time series data that are non-stationary and may have sharp changes like spikes. We propose an RNN-based model, called RNN-ODE-Adap, that uses a neural ODE to represent the time development of the hidden states, and we adaptively select time steps based on the steepness of changes of the data over time so as to train the model more efficiently for the "spike-like" time series. Theoretically, RNN-ODE-Adap yields provably a consistent estimation of the intensity function for the Hawkes-type time series data. We also provide an approximation analysis of the RNN-ODE model showing the benefit of adaptive steps. The proposed model is demonstrated to achieve higher prediction accuracy with reduced computational cost on simulated dynamic system data and point process data and on a real electrocardiography dataset.

Improving Adversarial Robustness by Contrastive Guided Diffusion Process

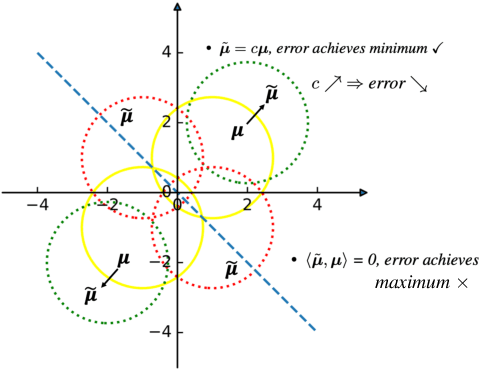
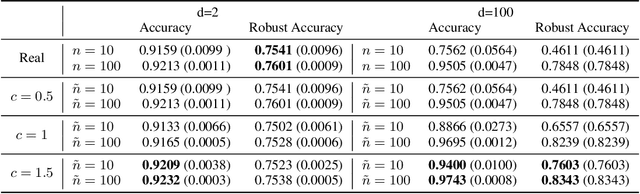
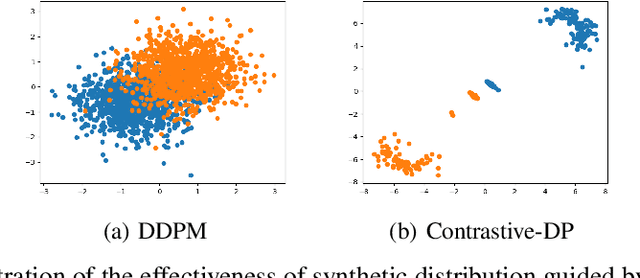
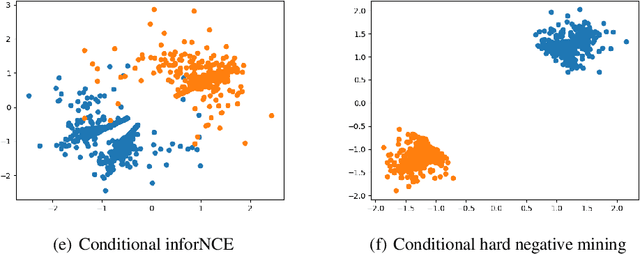
Synthetic data generation has become an emerging tool to help improve the adversarial robustness in classification tasks since robust learning requires a significantly larger amount of training samples compared with standard classification tasks. Among various deep generative models, the diffusion model has been shown to produce high-quality synthetic images and has achieved good performance in improving the adversarial robustness. However, diffusion-type methods are typically slow in data generation as compared with other generative models. Although different acceleration techniques have been proposed recently, it is also of great importance to study how to improve the sample efficiency of generated data for the downstream task. In this paper, we first analyze the optimality condition of synthetic distribution for achieving non-trivial robust accuracy. We show that enhancing the distinguishability among the generated data is critical for improving adversarial robustness. Thus, we propose the Contrastive-Guided Diffusion Process (Contrastive-DP), which adopts the contrastive loss to guide the diffusion model in data generation. We verify our theoretical results using simulations and demonstrate the good performance of Contrastive-DP on image datasets.

Generalizing to Unseen Domains with Wasserstein Distributional Robustness under Limited Source Knowledge

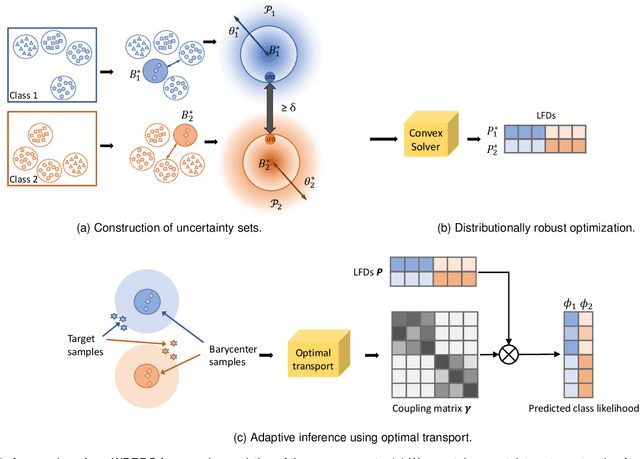
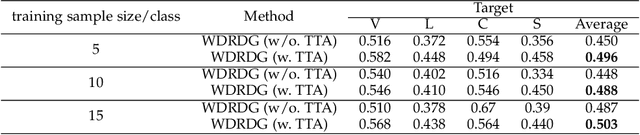
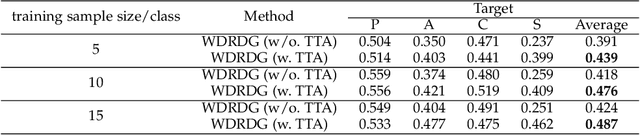
Domain generalization aims at learning a universal model that performs well on unseen target domains, incorporating knowledge from multiple source domains. In this research, we consider the scenario where different domain shifts occur among conditional distributions of different classes across domains. When labeled samples in the source domains are limited, existing approaches are not sufficiently robust. To address this problem, we propose a novel domain generalization framework called Wasserstein Distributionally Robust Domain Generalization (WDRDG), inspired by the concept of distributionally robust optimization. We encourage robustness over conditional distributions within class-specific Wasserstein uncertainty sets and optimize the worst-case performance of a classifier over these uncertainty sets. We further develop a test-time adaptation module leveraging optimal transport to quantify the relationship between the unseen target domain and source domains to make adaptive inference for target data. Experiments on the Rotated MNIST, PACS and the VLCS datasets demonstrate that our method could effectively balance the robustness and discriminability in challenging generalization scenarios.