Beyond Procedural Compliance: Human Oversight as a Dimension of Well-being Efficacy in AI Governance

Major AI ethics guidelines and laws, including the EU AI Act, call for effective human oversight, but do not define it as a distinct and developable capacity. This paper introduces human oversight as a well-being capacity, situated within the emerging Well-being Efficacy framework. The concept integrates AI literacy, ethical discernment, and awareness of human needs, acknowledging that some needs may be conflicting or harmful. Because people inevitably project desires, fears, and interests into AI systems, oversight requires the competence to examine and, when necessary, restrain problematic demands. The authors argue that the sustainable and cost-effective development of this capacity depends on its integration into education at every level, from professional training to lifelong learning. The frame of human oversight as a well-being capacity provides a practical path from high-level regulatory goals to the continuous cultivation of human agency and responsibility essential for safe and ethical AI. The paper establishes a theoretical foundation for future research on the pedagogical implementation and empirical validation of well-being effectiveness in multiple contexts.

Worst-case generation via minimax optimization in Wasserstein space

Worst-case generation plays a critical role in evaluating robustness and stress-testing systems under distribution shifts, in applications ranging from machine learning models to power grids and medical prediction systems. We develop a generative modeling framework for worst-case generation for a pre-specified risk, based on min-max optimization over continuous probability distributions, namely the Wasserstein space. Unlike traditional discrete distributionally robust optimization approaches, which often suffer from scalability issues, limited generalization, and costly worst-case inference, our framework exploits the Brenier theorem to characterize the least favorable (worst-case) distribution as the pushforward of a transport map from a continuous reference measure, enabling a continuous and expressive notion of risk-induced generation beyond classical discrete DRO formulations. Based on the min-max formulation, we propose a Gradient Descent Ascent (GDA)-type scheme that updates the decision model and the transport map in a single loop, establishing global convergence guarantees under mild regularity assumptions and possibly without convexity-concavity. We also propose to parameterize the transport map using a neural network that can be trained simultaneously with the GDA iterations by matching the transported training samples, thereby achieving a simulation-free approach. The efficiency of the proposed method as a risk-induced worst-case generator is validated by numerical experiments on synthetic and image data.

Scalable Gaussian Processes with Low-Rank Deep Kernel Decomposition

Kernels are key to encoding prior beliefs and data structures in Gaussian process (GP) models. The design of expressive and scalable kernels has garnered significant research attention. Deep kernel learning enhances kernel flexibility by feeding inputs through a neural network before applying a standard parametric form. However, this approach remains limited by the choice of base kernels, inherits high inference costs, and often demands sparse approximations. Drawing on Mercer's theorem, we introduce a fully data-driven, scalable deep kernel representation where a neural network directly represents a low-rank kernel through a small set of basis functions. This construction enables highly efficient exact GP inference in linear time and memory without invoking inducing points. It also supports scalable mini-batch training based on a principled variational inference framework. We further propose a simple variance correction procedure to guard against overconfidence in uncertainty estimates. Experiments on synthetic and real-world data demonstrate the advantages of our deep kernel GP in terms of predictive accuracy, uncertainty quantification, and computational efficiency.

PO-Flow: Flow-based Generative Models for Sampling Potential Outcomes and Counterfactuals

We propose PO-Flow, a novel continuous normalizing flow (CNF) framework for causal inference that jointly models potential outcomes and counterfactuals. Trained via flow matching, PO-Flow provides a unified framework for individualized potential outcome prediction, counterfactual predictions, and uncertainty-aware density learning. Among generative models, it is the first to enable density learning of potential outcomes without requiring explicit distributional assumptions (e.g., Gaussian mixtures), while also supporting counterfactual prediction conditioned on factual outcomes in general observational datasets. On benchmarks such as ACIC, IHDP, and IBM, it consistently outperforms prior methods across a range of causal inference tasks. Beyond that, PO-Flow succeeds in high-dimensional settings, including counterfactual image generation, demonstrating its broad applicability.

Modeling Discrete Coating Degradation Events via Hawkes Processes

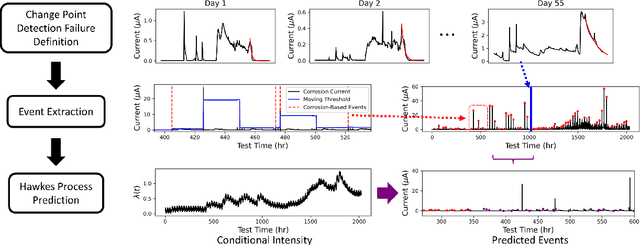
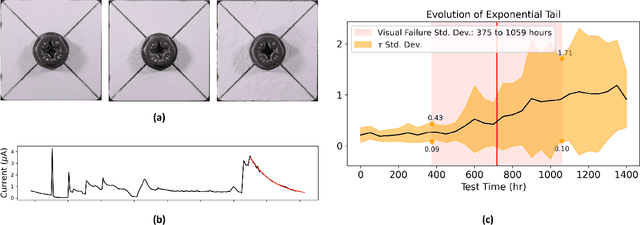
Forecasting the degradation of coated materials has long been a topic of critical interest in engineering, as it has enormous implications for both system maintenance and sustainable material use. Material degradation is affected by many factors, including the history of corrosion and characteristics of the environment, which can be measured by high-frequency sensors. However, the high volume of data produced by such sensors can inhibit efficient modeling and prediction. To alleviate this issue, we propose novel metrics for representing material degradation, taking the form of discrete degradation events. These events maintain the statistical properties of continuous sensor readings, such as correlation with time to coating failure and coefficient of variation at failure, but are composed of orders of magnitude fewer measurements. To forecast future degradation of the coating system, a marked Hawkes process models the events. We use the forecast of degradation to predict a future time of failure, exhibiting superior performance to the approach based on direct modeling of galvanic corrosion using continuous sensor measurements. While such maintenance is typically done on a regular basis, degradation models can enable informed condition-based maintenance, reducing unnecessary excess maintenance and preventing unexpected failures.

Graph-Based Prediction Models for Data Debiasing

Bias in data collection, arising from both under-reporting and over-reporting, poses significant challenges in critical applications such as healthcare and public safety. In this work, we introduce Graph-based Over- and Under-reporting Debiasing (GROUD), a novel graph-based optimization framework that debiases reported data by jointly estimating the true incident counts and the associated reporting bias probabilities. By modeling the bias as a smooth signal over a graph constructed from geophysical or feature-based similarities, our convex formulation not only ensures a unique solution but also comes with theoretical recovery guarantees under certain assumptions. We validate GROUD on both challenging simulated experiments and real-world datasets -- including Atlanta emergency calls and COVID-19 vaccine adverse event reports -- demonstrating its robustness and superior performance in accurately recovering debiased counts. This approach paves the way for more reliable downstream decision-making in systems affected by reporting irregularities.

Deep spatio-temporal point processes: Advances and new directions

Spatio-temporal point processes (STPPs) model discrete events distributed in time and space, with important applications in areas such as criminology, seismology, epidemiology, and social networks. Traditional models often rely on parametric kernels, limiting their ability to capture heterogeneous, nonstationary dynamics. Recent innovations integrate deep neural architectures -- either by modeling the conditional intensity function directly or by learning flexible, data-driven influence kernels, substantially broadening their expressive power. This article reviews the development of the deep influence kernel approach, which enjoys statistical explainability, since the influence kernel remains in the model to capture the spatiotemporal propagation of event influence and its impact on future events, while also possessing strong expressive power, thereby benefiting from both worlds. We explain the main components in developing deep kernel point processes, leveraging tools such as functional basis decomposition and graph neural networks to encode complex spatial or network structures, as well as estimation using both likelihood-based and likelihood-free methods, and address computational scalability for large-scale data. We also discuss the theoretical foundation of kernel identifiability. Simulated and real-data examples highlight applications to crime analysis, earthquake aftershock prediction, and sepsis prediction modeling, and we conclude by discussing promising directions for the field.

Sepsyn-OLCP: An Online Learning-based Framework for Early Sepsis Prediction with Uncertainty Quantification using Conformal Prediction

Sepsis is a life-threatening syndrome with high morbidity and mortality in hospitals. Early prediction of sepsis plays a crucial role in facilitating early interventions for septic patients. However, early sepsis prediction systems with uncertainty quantification and adaptive learning are scarce. This paper proposes Sepsyn-OLCP, a novel online learning algorithm for early sepsis prediction by integrating conformal prediction for uncertainty quantification and Bayesian bandits for adaptive decision-making. By combining the robustness of Bayesian models with the statistical uncertainty guarantees of conformal prediction methodologies, this algorithm delivers accurate and trustworthy predictions, addressing the critical need for reliable and adaptive systems in high-stakes healthcare applications such as early sepsis prediction. We evaluate the performance of Sepsyn-OLCP in terms of regret in stochastic bandit setting, the area under the receiver operating characteristic curve (AUROC), and F-measure. Our results show that Sepsyn-OLCP outperforms existing individual models, increasing AUROC of a neural network from 0.64 to 0.73 without retraining and high computational costs. And the model selection policy converges to the optimal strategy in the long run. We propose a novel reinforcement learning-based framework integrated with conformal prediction techniques to provide uncertainty quantification for early sepsis prediction. The proposed methodology delivers accurate and trustworthy predictions, addressing a critical need in high-stakes healthcare applications like early sepsis prediction.

Flow-based generative models as iterative algorithms in probability space

Generative AI (GenAI) has revolutionized data-driven modeling by enabling the synthesis of high-dimensional data across various applications, including image generation, language modeling, biomedical signal processing, and anomaly detection. Flow-based generative models provide a powerful framework for capturing complex probability distributions, offering exact likelihood estimation, efficient sampling, and deterministic transformations between distributions. These models leverage invertible mappings governed by Ordinary Differential Equations (ODEs), enabling precise density estimation and likelihood evaluation. This tutorial presents an intuitive mathematical framework for flow-based generative models, formulating them as neural network-based representations of continuous probability densities. We explore key theoretical principles, including the Wasserstein metric, gradient flows, and density evolution governed by ODEs, to establish convergence guarantees and bridge empirical advancements with theoretical insights. By providing a rigorous yet accessible treatment, we aim to equip researchers and practitioners with the necessary tools to effectively apply flow-based generative models in signal processing and machine learning.

Neural Spatiotemporal Point Processes: Trends and Challenges

Spatiotemporal point processes (STPPs) are probabilistic models for events occurring in continuous space and time. Real-world event data often exhibit intricate dependencies and heterogeneous dynamics. By incorporating modern deep learning techniques, STPPs can model these complexities more effectively than traditional approaches. Consequently, the fusion of neural methods with STPPs has become an active and rapidly evolving research area. In this review, we categorize existing approaches, unify key design choices, and explain the challenges of working with this data modality. We further highlight emerging trends and diverse application domains. Finally, we identify open challenges and gaps in the literature.