Optimization Landscape of Tucker Decomposition

Tucker decomposition is a popular technique for many data analysis and machine learning applications. Finding a Tucker decomposition is a nonconvex optimization problem. As the scale of the problems increases, local search algorithms such as stochastic gradient descent have become popular in practice. In this paper, we characterize the optimization landscape of the Tucker decomposition problem. In particular, we show that if the tensor has an exact Tucker decomposition, for a standard nonconvex objective of Tucker decomposition, all local minima are also globally optimal. We also give a local search algorithm that can find an approximate local (and global) optimal solution in polynomial time.

Extracting Latent State Representations with Linear Dynamics from Rich Observations

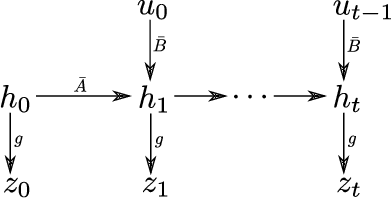
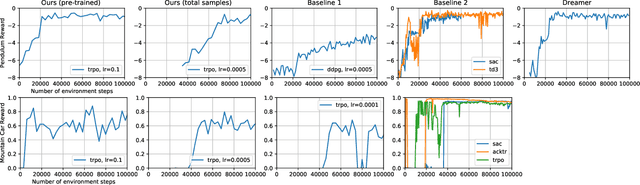
Recently, many reinforcement learning techniques were shown to have provable guarantees in the simple case of linear dynamics, especially in problems like linear quadratic regulators. However, in practice, many reinforcement learning problems try to learn a policy directly from rich, high dimensional representations such as images. Even if there is an underlying dynamics that is linear in the correct latent representations (such as position and velocity), the rich representation is likely to be nonlinear and can contain irrelevant features. In this work we study a model where there is a hidden linear subspace in which the dynamics is linear. For such a model we give an efficient algorithm for extracting the linear subspace with linear dynamics. We then extend our idea to extracting a nonlinear mapping, and empirically verify the effectiveness of our approach in simple settings with rich observations.

Energy-Aware DNN Graph Optimization

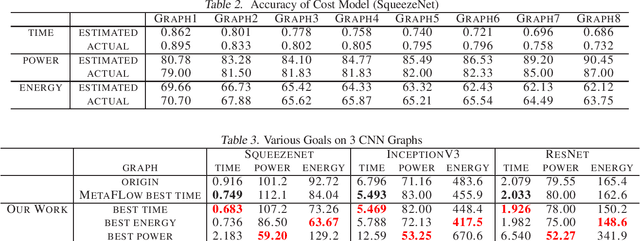
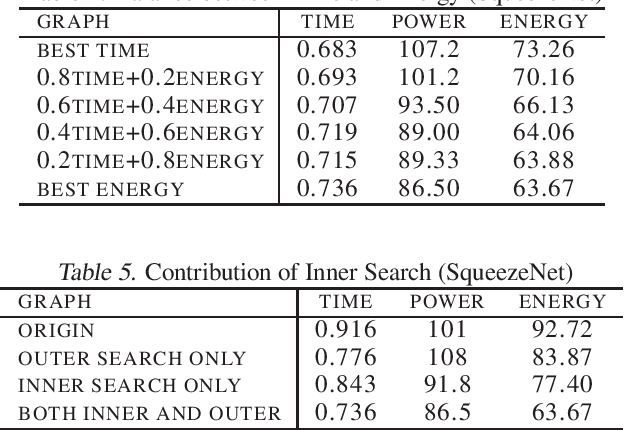
Unlike existing work in deep neural network (DNN) graphs optimization for inference performance, we explore DNN graph optimization for energy awareness and savings for power- and resource-constrained machine learning devices. We present a method that allows users to optimize energy consumption or balance between energy and inference performance for DNN graphs. This method efficiently searches through the space of equivalent graphs, and identifies a graph and the corresponding algorithms that incur the least cost in execution. We implement the method and evaluate it with multiple DNN models on a GPU-based machine. Results show that our method achieves significant energy savings, i.e., 24% with negligible performance impact.

High-Dimensional Robust Mean Estimation via Gradient Descent

We study the problem of high-dimensional robust mean estimation in the presence of a constant fraction of adversarial outliers. A recent line of work has provided sophisticated polynomial-time algorithms for this problem with dimension-independent error guarantees for a range of natural distribution families. In this work, we show that a natural non-convex formulation of the problem can be solved directly by gradient descent. Our approach leverages a novel structural lemma, roughly showing that any approximate stationary point of our non-convex objective gives a near-optimal solution to the underlying robust estimation task. Our work establishes an intriguing connection between algorithmic high-dimensional robust statistics and non-convex optimization, which may have broader applications to other robust estimation tasks.

Spectral Learning on Matrices and Tensors

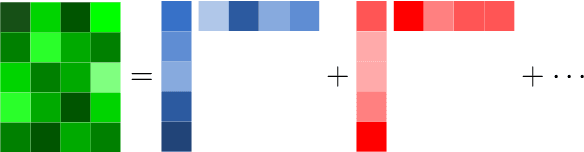
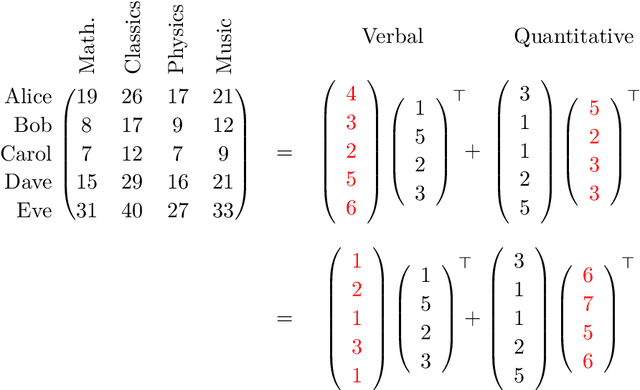
Spectral methods have been the mainstay in several domains such as machine learning and scientific computing. They involve finding a certain kind of spectral decomposition to obtain basis functions that can capture important structures for the problem at hand. The most common spectral method is the principal component analysis (PCA). It utilizes the top eigenvectors of the data covariance matrix, e.g. to carry out dimensionality reduction. This data pre-processing step is often effective in separating signal from noise. PCA and other spectral techniques applied to matrices have several limitations. By limiting to only pairwise moments, they are effectively making a Gaussian approximation on the underlying data and fail on data with hidden variables which lead to non-Gaussianity. However, in most data sets, there are latent effects that cannot be directly observed, e.g., topics in a document corpus, or underlying causes of a disease. By extending the spectral decomposition methods to higher order moments, we demonstrate the ability to learn a wide range of latent variable models efficiently. Higher-order moments can be represented by tensors, and intuitively, they can encode more information than just pairwise moment matrices. More crucially, tensor decomposition can pick up latent effects that are missed by matrix methods, e.g. uniquely identify non-orthogonal components. Exploiting these aspects turns out to be fruitful for provable unsupervised learning of a wide range of latent variable models. We also outline the computational techniques to design efficient tensor decomposition methods. We introduce Tensorly, which has a simple python interface for expressing tensor operations. It has a flexible back-end system supporting NumPy, PyTorch, TensorFlow and MXNet amongst others, allowing multi-GPU and CPU operations and seamless integration with deep-learning functionalities.

Estimating Normalizing Constants for Log-Concave Distributions: Algorithms and Lower Bounds

Estimating the normalizing constant of an unnormalized probability distribution has important applications in computer science, statistical physics, machine learning, and statistics. In this work, we consider the problem of estimating the normalizing constant $Z=\int_{\mathbb{R}^d} e^{-f(x)}\,\mathrm{d}x$ to within a multiplication factor of $1 \pm \varepsilon$ for a $\mu$-strongly convex and $L$-smooth function $f$, given query access to $f(x)$ and $\nabla f(x)$. We give both algorithms and lowerbounds for this problem. Using an annealing algorithm combined with a multilevel Monte Carlo method based on underdamped Langevin dynamics, we show that $\widetilde{\mathcal{O}}\Bigl(\frac{d^{4/3}\kappa + d^{7/6}\kappa^{7/6}}{\varepsilon^2}\Bigr)$ queries to $\nabla f$ are sufficient, where $\kappa= L / \mu$ is the condition number. Moreover, we provide an information theoretic lowerbound, showing that at least $\frac{d^{1-o(1)}}{\varepsilon^{2-o(1)}}$ queries are necessary. This provides a first nontrivial lowerbound for the problem.

Mildly Overparametrized Neural Nets can Memorize Training Data Efficiently

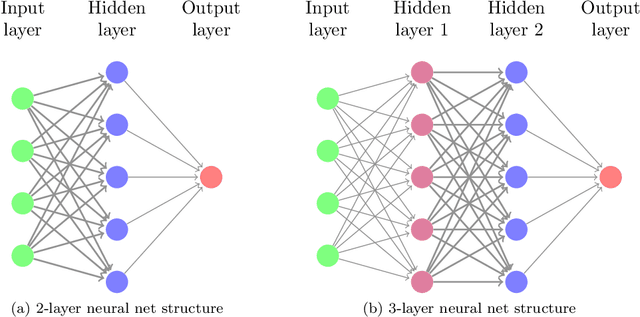
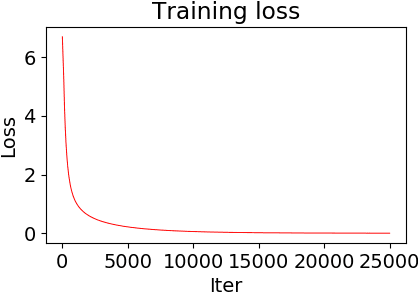
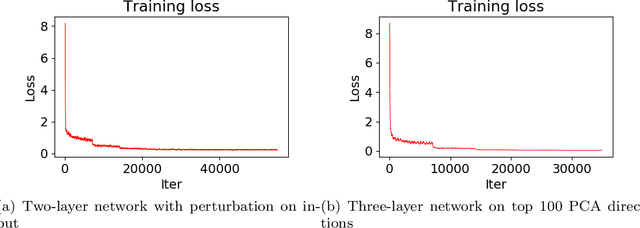
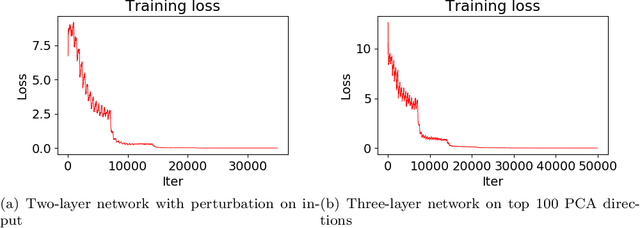
It has been observed \citep{zhang2016understanding} that deep neural networks can memorize: they achieve 100\% accuracy on training data. Recent theoretical results explained such behavior in highly overparametrized regimes, where the number of neurons in each layer is larger than the number of training samples. In this paper, we show that neural networks can be trained to memorize training data perfectly in a mildly overparametrized regime, where the number of parameters is just a constant factor more than the number of training samples, and the number of neurons is much smaller.

Explaining Landscape Connectivity of Low-cost Solutions for Multilayer Nets

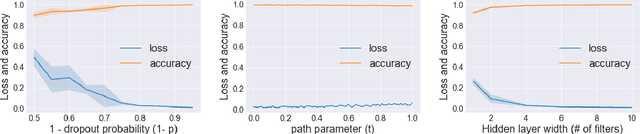
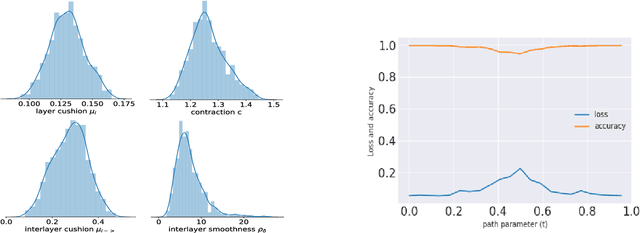
Mode connectivity is a surprising phenomenon in the loss landscape of deep nets. Optima---at least those discovered by gradient-based optimization---turn out to be connected by simple paths on which the loss function is almost constant. Often, these paths can be chosen to be piece-wise linear, with as few as two segments. We give mathematical explanations for this phenomenon, assuming generic properties (such as dropout stability and noise stability) of well-trained deep nets, which have previously been identified as part of understanding the generalization properties of deep nets. Our explanation holds for realistic multilayer nets, and experiments are presented to verify the theory.

Faster Algorithms for High-Dimensional Robust Covariance Estimation

We study the problem of estimating the covariance matrix of a high-dimensional distribution when a small constant fraction of the samples can be arbitrarily corrupted. Recent work gave the first polynomial time algorithms for this problem with near-optimal error guarantees for several natural structured distributions. Our main contribution is to develop faster algorithms for this problem whose running time nearly matches that of computing the empirical covariance. Given $N = \tilde{\Omega}(d^2/\epsilon^2)$ samples from a $d$-dimensional Gaussian distribution, an $\epsilon$-fraction of which may be arbitrarily corrupted, our algorithm runs in time $\tilde{O}(d^{3.26})/\mathrm{poly}(\epsilon)$ and approximates the unknown covariance matrix to optimal error up to a logarithmic factor. Previous robust algorithms with comparable error guarantees all have runtimes $\tilde{\Omega}(d^{2 \omega})$ when $\epsilon = \Omega(1)$, where $\omega$ is the exponent of matrix multiplication. We also provide evidence that improving the running time of our algorithm may require new algorithmic techniques.

Stabilized SVRG: Simple Variance Reduction for Nonconvex Optimization

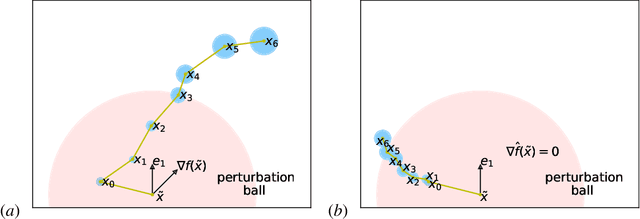
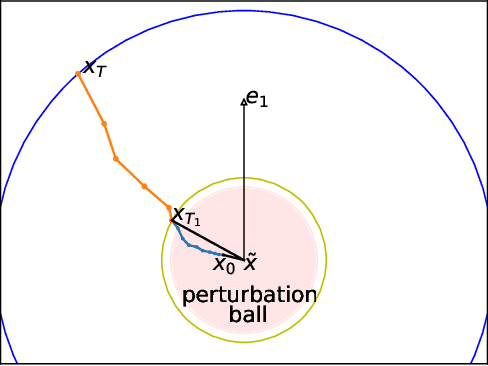
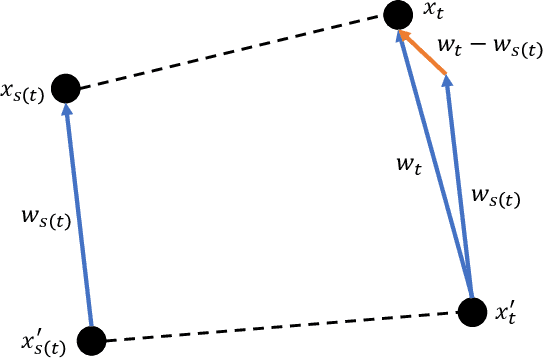
Variance reduction techniques like SVRG provide simple and fast algorithms for optimizing a convex finite-sum objective. For nonconvex objectives, these techniques can also find a first-order stationary point (with small gradient). However, in nonconvex optimization it is often crucial to find a second-order stationary point (with small gradient and almost PSD hessian). In this paper, we show that Stabilized SVRG (a simple variant of SVRG) can find an $\epsilon$-second-order stationary point using only $\widetilde{O}(n^{2/3}/\epsilon^2+n/\epsilon^{1.5})$ stochastic gradients. To our best knowledge, this is the first second-order guarantee for a simple variant of SVRG. The running time almost matches the known guarantees for finding $\epsilon$-first-order stationary points.