Independence Tests for Language Models

We consider the following problem: given the weights of two models, can we test whether they were trained independently -- i.e., from independent random initializations? We consider two settings: constrained and unconstrained. In the constrained setting, we make assumptions about model architecture and training and propose a family of statistical tests that yield exact p-values with respect to the null hypothesis that the models are trained from independent random initializations. These p-values are valid regardless of the composition of either model's training data; we compute them by simulating exchangeable copies of each model under our assumptions and comparing various similarity measures of weights and activations between the original two models versus these copies. We report the p-values from these tests on pairs of 21 open-weight models (210 total pairs) and correctly identify all pairs of non-independent models. Our tests remain effective even if one model was fine-tuned for many tokens. In the unconstrained setting, where we make no assumptions about training procedures, can change model architecture, and allow for adversarial evasion attacks, the previous tests no longer work. Instead, we propose a new test which matches hidden activations between two models, and which is robust to adversarial transformations and to changes in model architecture. The test can also do localized testing: identifying specific non-independent components of models. Though we no longer obtain exact p-values from this, empirically we find it behaves as one and reliably identifies non-independent models. Notably, we can use the test to identify specific parts of one model that are derived from another (e.g., how Llama 3.1-8B was pruned to initialize Llama 3.2-3B, or shared layers between Mistral-7B and StripedHyena-7B), and it is even robust to retraining individual layers of either model from scratch.

Auditing Prompt Caching in Language Model APIs

Prompt caching in large language models (LLMs) results in data-dependent timing variations: cached prompts are processed faster than non-cached prompts. These timing differences introduce the risk of side-channel timing attacks. For example, if the cache is shared across users, an attacker could identify cached prompts from fast API response times to learn information about other users' prompts. Because prompt caching may cause privacy leakage, transparency around the caching policies of API providers is important. To this end, we develop and conduct statistical audits to detect prompt caching in real-world LLM API providers. We detect global cache sharing across users in seven API providers, including OpenAI, resulting in potential privacy leakage about users' prompts. Timing variations due to prompt caching can also result in leakage of information about model architecture. Namely, we find evidence that OpenAI's embedding model is a decoder-only Transformer, which was previously not publicly known.

Resampling methods for Private Statistical Inference

We consider the task of constructing confidence intervals with differential privacy. We propose two private variants of the non-parametric bootstrap, which privately compute the median of the results of multiple ``little'' bootstraps run on partitions of the data and give asymptotic bounds on the coverage error of the resulting confidence intervals. For a fixed differential privacy parameter $\epsilon$, our methods enjoy the same error rates as that of the non-private bootstrap to within logarithmic factors in the sample size $n$. We empirically validate the performance of our methods for mean estimation, median estimation, and logistic regression with both real and synthetic data. Our methods achieve similar coverage accuracy to existing methods (and non-private baselines) while providing notably shorter ($\gtrsim 10$ times) confidence intervals than previous approaches.

Robust Distortion-free Watermarks for Language Models

We propose a methodology for planting watermarks in text from an autoregressive language model that are robust to perturbations without changing the distribution over text up to a certain maximum generation budget. We generate watermarked text by mapping a sequence of random numbers -- which we compute using a randomized watermark key -- to a sample from the language model. To detect watermarked text, any party who knows the key can align the text to the random number sequence. We instantiate our watermark methodology with two sampling schemes: inverse transform sampling and exponential minimum sampling. We apply these watermarks to three language models -- OPT-1.3B, LLaMA-7B and Alpaca-7B -- to experimentally validate their statistical power and robustness to various paraphrasing attacks. Notably, for both the OPT-1.3B and LLaMA-7B models, we find we can reliably detect watermarked text ($p \leq 0.01$) from $35$ tokens even after corrupting between $40$-$50$\% of the tokens via random edits (i.e., substitutions, insertions or deletions). For the Alpaca-7B model, we conduct a case study on the feasibility of watermarking responses to typical user instructions. Due to the lower entropy of the responses, detection is more difficult: around $25\%$ of the responses -- whose median length is around $100$ tokens -- are detectable with $p \leq 0.01$, and the watermark is also less robust to certain automated paraphrasing attacks we implement.

A Fast Algorithm for Adaptive Private Mean Estimation

We design an $(\varepsilon, \delta)$-differentially private algorithm to estimate the mean of a $d$-variate distribution, with unknown covariance $\Sigma$, that is adaptive to $\Sigma$. To within polylogarithmic factors, the estimator achieves optimal rates of convergence with respect to the induced Mahalanobis norm $||\cdot||_\Sigma$, takes time $\tilde{O}(n d^2)$ to compute, has near linear sample complexity for sub-Gaussian distributions, allows $\Sigma$ to be degenerate or low rank, and adaptively extends beyond sub-Gaussianity. Prior to this work, other methods required exponential computation time or the superlinear scaling $n = \Omega(d^{3/2})$ to achieve non-trivial error with respect to the norm $||\cdot||_\Sigma$.

Memorize to Generalize: on the Necessity of Interpolation in High Dimensional Linear Regression

We examine the necessity of interpolation in overparameterized models, that is, when achieving optimal predictive risk in machine learning problems requires (nearly) interpolating the training data. In particular, we consider simple overparameterized linear regression $y = X \theta + w$ with random design $X \in \mathbb{R}^{n \times d}$ under the proportional asymptotics $d/n \to \gamma \in (1, \infty)$. We precisely characterize how prediction (test) error necessarily scales with training error in this setting. An implication of this characterization is that as the label noise variance $\sigma^2 \to 0$, any estimator that incurs at least $\mathsf{c}\sigma^4$ training error for some constant $\mathsf{c}$ is necessarily suboptimal and will suffer growth in excess prediction error at least linear in the training error. Thus, optimal performance requires fitting training data to substantially higher accuracy than the inherent noise floor of the problem.

On the Opportunities and Risks of Foundation Models

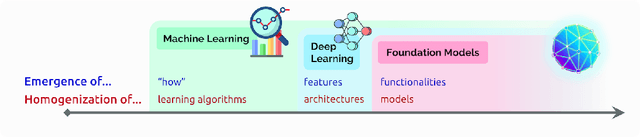
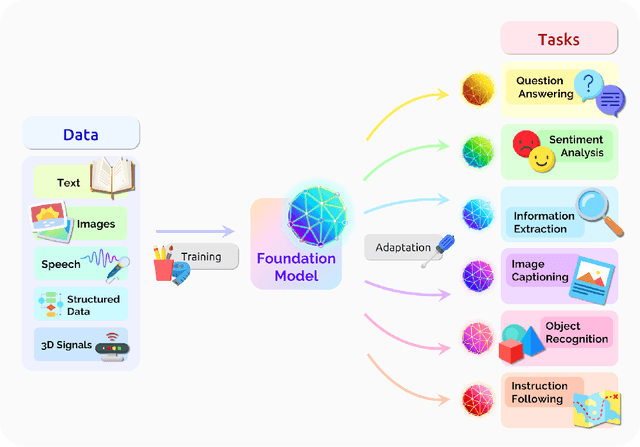
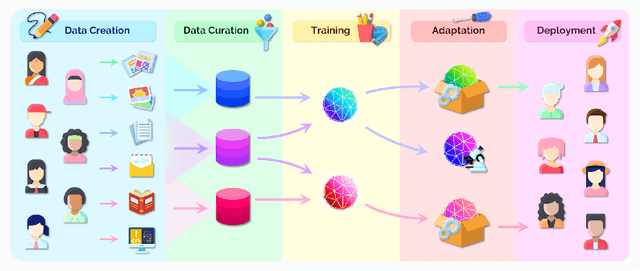
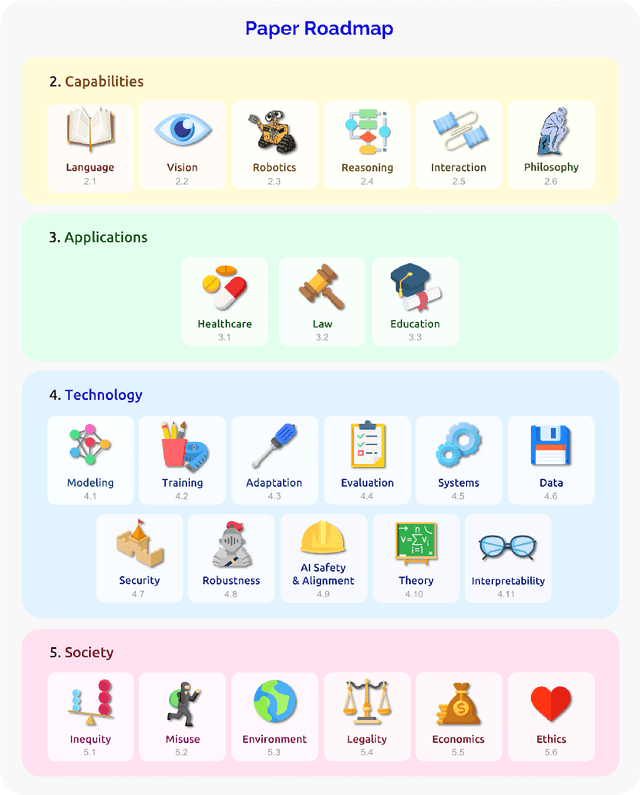
AI is undergoing a paradigm shift with the rise of models (e.g., BERT, DALL-E, GPT-3) that are trained on broad data at scale and are adaptable to a wide range of downstream tasks. We call these models foundation models to underscore their critically central yet incomplete character. This report provides a thorough account of the opportunities and risks of foundation models, ranging from their capabilities (e.g., language, vision, robotics, reasoning, human interaction) and technical principles(e.g., model architectures, training procedures, data, systems, security, evaluation, theory) to their applications (e.g., law, healthcare, education) and societal impact (e.g., inequity, misuse, economic and environmental impact, legal and ethical considerations). Though foundation models are based on standard deep learning and transfer learning, their scale results in new emergent capabilities,and their effectiveness across so many tasks incentivizes homogenization. Homogenization provides powerful leverage but demands caution, as the defects of the foundation model are inherited by all the adapted models downstream. Despite the impending widespread deployment of foundation models, we currently lack a clear understanding of how they work, when they fail, and what they are even capable of due to their emergent properties. To tackle these questions, we believe much of the critical research on foundation models will require deep interdisciplinary collaboration commensurate with their fundamentally sociotechnical nature.

Explaining Landscape Connectivity of Low-cost Solutions for Multilayer Nets

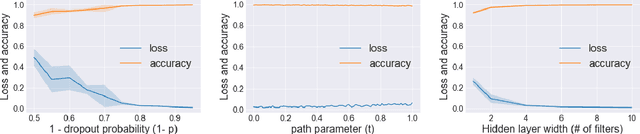
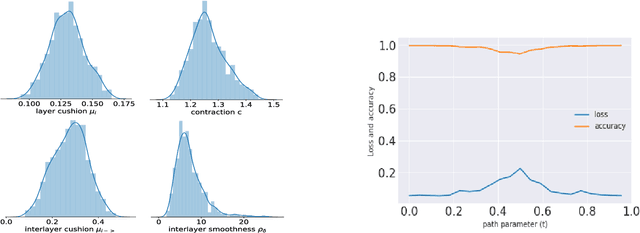
Mode connectivity is a surprising phenomenon in the loss landscape of deep nets. Optima---at least those discovered by gradient-based optimization---turn out to be connected by simple paths on which the loss function is almost constant. Often, these paths can be chosen to be piece-wise linear, with as few as two segments. We give mathematical explanations for this phenomenon, assuming generic properties (such as dropout stability and noise stability) of well-trained deep nets, which have previously been identified as part of understanding the generalization properties of deep nets. Our explanation holds for realistic multilayer nets, and experiments are presented to verify the theory.

Learning Two-layer Neural Networks with Symmetric Inputs

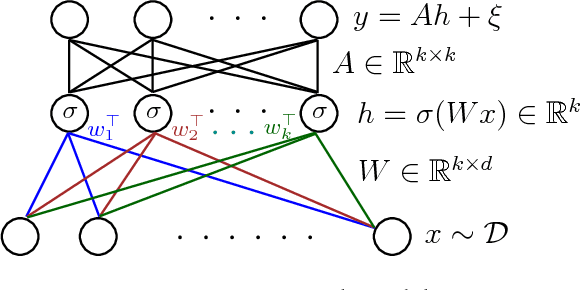
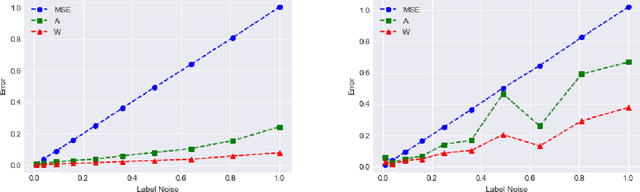
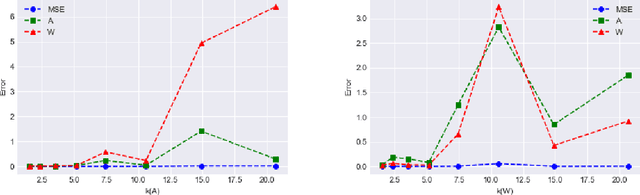
We give a new algorithm for learning a two-layer neural network under a general class of input distributions. Assuming there is a ground-truth two-layer network $$ y = A \sigma(Wx) + \xi, $$ where $A,W$ are weight matrices, $\xi$ represents noise, and the number of neurons in the hidden layer is no larger than the input or output, our algorithm is guaranteed to recover the parameters $A,W$ of the ground-truth network. The only requirement on the input $x$ is that it is symmetric, which still allows highly complicated and structured input. Our algorithm is based on the method-of-moments framework and extends several results in tensor decompositions. We use spectral algorithms to avoid the complicated non-convex optimization in learning neural networks. Experiments show that our algorithm can robustly learn the ground-truth neural network with a small number of samples for many symmetric input distributions.