Optimization Landscape of Tucker Decomposition

Tucker decomposition is a popular technique for many data analysis and machine learning applications. Finding a Tucker decomposition is a nonconvex optimization problem. As the scale of the problems increases, local search algorithms such as stochastic gradient descent have become popular in practice. In this paper, we characterize the optimization landscape of the Tucker decomposition problem. In particular, we show that if the tensor has an exact Tucker decomposition, for a standard nonconvex objective of Tucker decomposition, all local minima are also globally optimal. We also give a local search algorithm that can find an approximate local (and global) optimal solution in polynomial time.

Extracting Latent State Representations with Linear Dynamics from Rich Observations

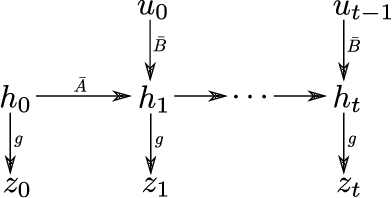
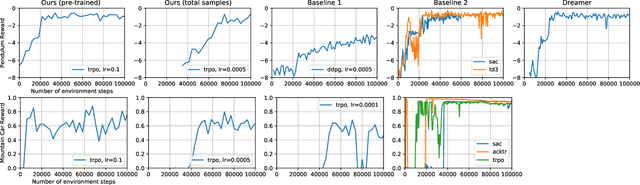
Recently, many reinforcement learning techniques were shown to have provable guarantees in the simple case of linear dynamics, especially in problems like linear quadratic regulators. However, in practice, many reinforcement learning problems try to learn a policy directly from rich, high dimensional representations such as images. Even if there is an underlying dynamics that is linear in the correct latent representations (such as position and velocity), the rich representation is likely to be nonlinear and can contain irrelevant features. In this work we study a model where there is a hidden linear subspace in which the dynamics is linear. For such a model we give an efficient algorithm for extracting the linear subspace with linear dynamics. We then extend our idea to extracting a nonlinear mapping, and empirically verify the effectiveness of our approach in simple settings with rich observations.

Understanding Composition of Word Embeddings via Tensor Decomposition

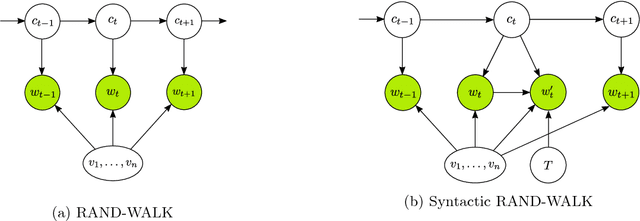
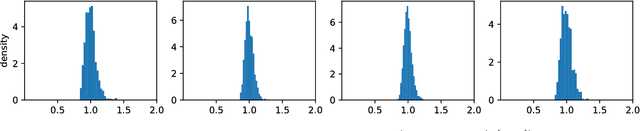
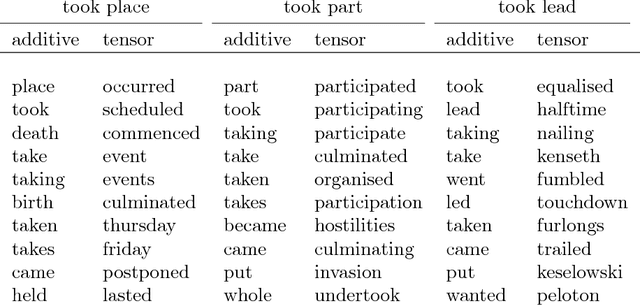
Word embedding is a powerful tool in natural language processing. In this paper we consider the problem of word embedding composition \--- given vector representations of two words, compute a vector for the entire phrase. We give a generative model that can capture specific syntactic relations between words. Under our model, we prove that the correlations between three words (measured by their PMI) form a tensor that has an approximate low rank Tucker decomposition. The result of the Tucker decomposition gives the word embeddings as well as a core tensor, which can be used to produce better compositions of the word embeddings. We also complement our theoretical results with experiments that verify our assumptions, and demonstrate the effectiveness of the new composition method.