Progressive distillation induces an implicit curriculum

Knowledge distillation leverages a teacher model to improve the training of a student model. A persistent challenge is that a better teacher does not always yield a better student, to which a common mitigation is to use additional supervision from several ``intermediate'' teachers. One empirically validated variant of this principle is progressive distillation, where the student learns from successive intermediate checkpoints of the teacher. Using sparse parity as a sandbox, we identify an implicit curriculum as one mechanism through which progressive distillation accelerates the student's learning. This curriculum is available only through the intermediate checkpoints but not the final converged one, and imparts both empirical acceleration and a provable sample complexity benefit to the student. We then extend our investigation to Transformers trained on probabilistic context-free grammars (PCFGs) and real-world pre-training datasets (Wikipedia and Books). Through probing the teacher model, we identify an analogous implicit curriculum where the model progressively learns features that capture longer context. Our theoretical and empirical findings on sparse parity, complemented by empirical observations on more complex tasks, highlight the benefit of progressive distillation via implicit curriculum across setups.

TinyGSM: achieving >80% on GSM8k with small language models

Small-scale models offer various computational advantages, and yet to which extent size is critical for problem-solving abilities remains an open question. Specifically for solving grade school math, the smallest model size so far required to break the 80\% barrier on the GSM8K benchmark remains to be 34B. Our work studies how high-quality datasets may be the key for small language models to acquire mathematical reasoning. We introduce \texttt{TinyGSM}, a synthetic dataset of 12.3M grade school math problems paired with Python solutions, generated fully by GPT-3.5. After finetuning on \texttt{TinyGSM}, we find that a duo of a 1.3B generation model and a 1.3B verifier model can achieve 81.5\% accuracy, outperforming existing models that are orders of magnitude larger. This also rivals the performance of the GPT-3.5 ``teacher'' model (77.4\%), from which our model's training data is generated. Our approach is simple and has two key components: 1) the high-quality dataset \texttt{TinyGSM}, 2) the use of a verifier, which selects the final outputs from multiple candidate generations.

Transformers are uninterpretable with myopic methods: a case study with bounded Dyck grammars

Interpretability methods aim to understand the algorithm implemented by a trained model (e.g., a Transofmer) by examining various aspects of the model, such as the weight matrices or the attention patterns. In this work, through a combination of theoretical results and carefully controlled experiments on synthetic data, we take a critical view of methods that exclusively focus on individual parts of the model, rather than consider the network as a whole. We consider a simple synthetic setup of learning a (bounded) Dyck language. Theoretically, we show that the set of models that (exactly or approximately) solve this task satisfy a structural characterization derived from ideas in formal languages (the pumping lemma). We use this characterization to show that the set of optima is qualitatively rich; in particular, the attention pattern of a single layer can be ``nearly randomized'', while preserving the functionality of the network. We also show via extensive experiments that these constructions are not merely a theoretical artifact: even after severely constraining the architecture of the model, vastly different solutions can be reached via standard training. Thus, interpretability claims based on inspecting individual heads or weight matrices in the Transformer can be misleading.

Understanding Augmentation-based Self-Supervised Representation Learning via RKHS Approximation

Good data augmentation is one of the key factors that lead to the empirical success of self-supervised representation learning such as contrastive learning and masked language modeling, yet theoretical understanding of its role in learning good representations remains limited. Recent work has built the connection between self-supervised learning and approximating the top eigenspace of a graph Laplacian operator. Learning a linear probe on top of such features can naturally be connected to RKHS regression. In this work, we use this insight to perform a statistical analysis of augmentation-based pretraining. We start from the isometry property, a key geometric characterization of the target function given by the augmentation. Our first main theorem provides, for an arbitrary encoder, near tight bounds for both the estimation error incurred by fitting the linear probe on top of the encoder, and the approximation error entailed by the fitness of the RKHS the encoder learns. Our second main theorem specifically addresses the case where the encoder extracts the top-d eigenspace of a Monte-Carlo approximation of the underlying kernel with the finite pretraining samples. Our analysis completely disentangles the effects of the model and the augmentation. A key ingredient in our analysis is the augmentation complexity, which we use to quantitatively compare different augmentations and analyze their impact on downstream performance on synthetic and real datasets.

Exposing Attention Glitches with Flip-Flop Language Modeling

Why do large language models sometimes output factual inaccuracies and exhibit erroneous reasoning? The brittleness of these models, particularly when executing long chains of reasoning, currently seems to be an inevitable price to pay for their advanced capabilities of coherently synthesizing knowledge, pragmatics, and abstract thought. Towards making sense of this fundamentally unsolved problem, this work identifies and analyzes the phenomenon of attention glitches, in which the Transformer architecture's inductive biases intermittently fail to capture robust reasoning. To isolate the issue, we introduce flip-flop language modeling (FFLM), a parametric family of synthetic benchmarks designed to probe the extrapolative behavior of neural language models. This simple generative task requires a model to copy binary symbols over long-range dependencies, ignoring the tokens in between. We find that Transformer FFLMs suffer from a long tail of sporadic reasoning errors, some of which we can eliminate using various regularization techniques. Our preliminary mechanistic analyses show why the remaining errors may be very difficult to diagnose and resolve. We hypothesize that attention glitches account for (some of) the closed-domain hallucinations in natural LLMs.

Transformers Learn Shortcuts to Automata

Algorithmic reasoning requires capabilities which are most naturally understood through recurrent models of computation, like the Turing machine. However, Transformer models, while lacking recurrence, are able to perform such reasoning using far fewer layers than the number of reasoning steps. This raises the question: what solutions are these shallow and non-recurrent models finding? We investigate this question in the setting of learning automata, discrete dynamical systems naturally suited to recurrent modeling and expressing algorithmic tasks. Our theoretical results completely characterize shortcut solutions, whereby a shallow Transformer with only $o(T)$ layers can exactly replicate the computation of an automaton on an input sequence of length $T$. By representing automata using the algebraic structure of their underlying transformation semigroups, we obtain $O(\log T)$-depth simulators for all automata and $O(1)$-depth simulators for all automata whose associated groups are solvable. Empirically, we perform synthetic experiments by training Transformers to simulate a wide variety of automata, and show that shortcut solutions can be learned via standard training. We further investigate the brittleness of these solutions and propose potential mitigations.

Masked prediction tasks: a parameter identifiability view

The vast majority of work in self-supervised learning, both theoretical and empirical (though mostly the latter), have largely focused on recovering good features for downstream tasks, with the definition of "good" often being intricately tied to the downstream task itself. This lens is undoubtedly very interesting, but suffers from the problem that there isn't a "canonical" set of downstream tasks to focus on -- in practice, this problem is usually resolved by competing on the benchmark dataset du jour. In this paper, we present an alternative lens: one of parameter identifiability. More precisely, we consider data coming from a parametric probabilistic model, and train a self-supervised learning predictor with a suitably chosen parametric form. Then, we ask whether we can read off the ground truth parameters of the probabilistic model from the optimal predictor. We focus on the widely used self-supervised learning method of predicting masked tokens, which is popular for both natural languages and visual data. While incarnations of this approach have already been successfully used for simpler probabilistic models (e.g. learning fully-observed undirected graphical models), we focus instead on latent-variable models capturing sequential structures -- namely Hidden Markov Models with both discrete and conditionally Gaussian observations. We show that there is a rich landscape of possibilities, out of which some prediction tasks yield identifiability, while others do not. Our results, borne of a theoretical grounding of self-supervised learning, could thus potentially beneficially inform practice. Moreover, we uncover close connections with uniqueness of tensor rank decompositions -- a widely used tool in studying identifiability through the lens of the method of moments.

Analyzing and Improving the Optimization Landscape of Noise-Contrastive Estimation

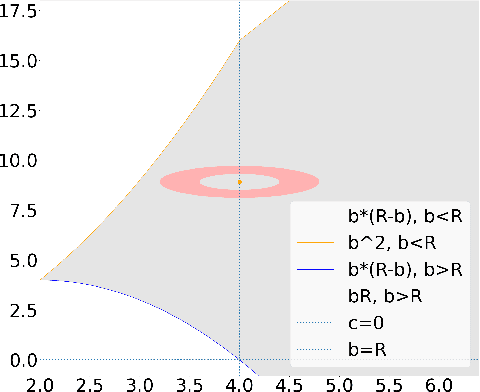
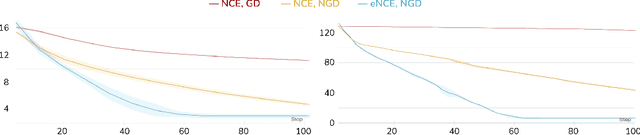
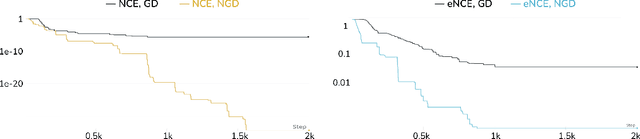
Noise-contrastive estimation (NCE) is a statistically consistent method for learning unnormalized probabilistic models. It has been empirically observed that the choice of the noise distribution is crucial for NCE's performance. However, such observations have never been made formal or quantitative. In fact, it is not even clear whether the difficulties arising from a poorly chosen noise distribution are statistical or algorithmic in nature. In this work, we formally pinpoint reasons for NCE's poor performance when an inappropriate noise distribution is used. Namely, we prove these challenges arise due to an ill-behaved (more precisely, flat) loss landscape. To address this, we introduce a variant of NCE called "eNCE" which uses an exponential loss and for which normalized gradient descent addresses the landscape issues provably when the target and noise distributions are in a given exponential family.

Contrastive learning of strong-mixing continuous-time stochastic processes

Contrastive learning is a family of self-supervised methods where a model is trained to solve a classification task constructed from unlabeled data. It has recently emerged as one of the leading learning paradigms in the absence of labels across many different domains (e.g. brain imaging, text, images). However, theoretical understanding of many aspects of training, both statistical and algorithmic, remain fairly elusive. In this work, we study the setting of time series -- more precisely, when we get data from a strong-mixing continuous-time stochastic process. We show that a properly constructed contrastive learning task can be used to estimate the transition kernel for small-to-mid-range intervals in the diffusion case. Moreover, we give sample complexity bounds for solving this task and quantitatively characterize what the value of the contrastive loss implies for distributional closeness of the learned kernel. As a byproduct, we illuminate the appropriate settings for the contrastive distribution, as well as other hyperparameters in this setup.

Spatiotemporal Relationship Reasoning for Pedestrian Intent Prediction

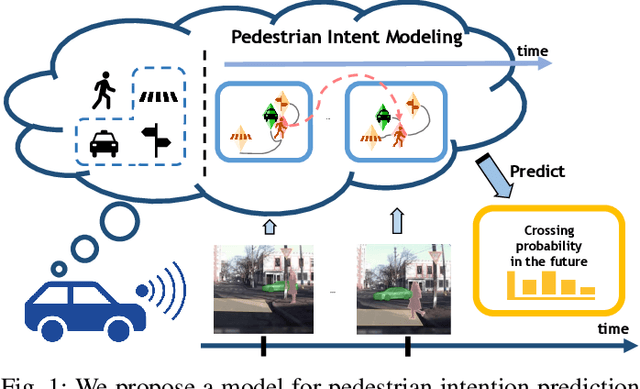
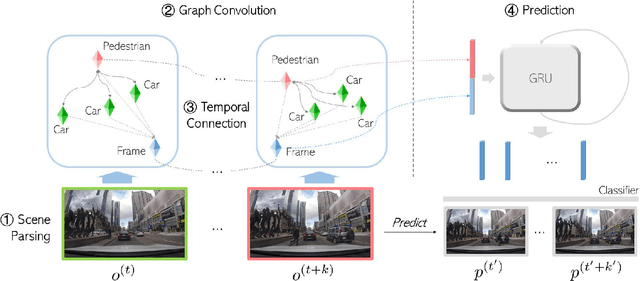
Reasoning over visual data is a desirable capability for robotics and vision-based applications. Such reasoning enables forecasting of the next events or actions in videos. In recent years, various models have been developed based on convolution operations for prediction or forecasting, but they lack the ability to reason over spatiotemporal data and infer the relationships of different objects in the scene. In this paper, we present a framework based on graph convolution to uncover the spatiotemporal relationships in the scene for reasoning about pedestrian intent. A scene graph is built on top of segmented object instances within and across video frames. Pedestrian intent, defined as the future action of crossing or not-crossing the street, is a very crucial piece of information for autonomous vehicles to navigate safely and more smoothly. We approach the problem of intent prediction from two different perspectives and anticipate the intention-to-cross within both pedestrian-centric and location-centric scenarios. In addition, we introduce a new dataset designed specifically for autonomous-driving scenarios in areas with dense pedestrian populations: the Stanford-TRI Intent Prediction (STIP) dataset. Our experiments on STIP and another benchmark dataset show that our graph modeling framework is able to predict the intention-to-cross of the pedestrians with an accuracy of 79.10% on STIP and 79.28% on \rev{Joint Attention for Autonomous Driving (JAAD) dataset up to one second earlier than when the actual crossing happens. These results outperform the baseline and previous work. Please refer to http://stip.stanford.edu/ for the dataset and code.