Clustering in Deep Stochastic Transformers

Transformers have revolutionized deep learning across various domains but understanding the precise token dynamics remains a theoretical challenge. Existing theories of deep Transformers with layer normalization typically predict that tokens cluster to a single point; however, these results rely on deterministic weight assumptions, which fail to capture the standard initialization scheme in Transformers. In this work, we show that accounting for the intrinsic stochasticity of random initialization alters this picture. More precisely, we analyze deep Transformers where noise arises from the random initialization of value matrices. Under diffusion scaling and token-wise RMS normalization, we prove that, as the number of Transformer layers goes to infinity, the discrete token dynamics converge to an interacting-particle system on the sphere where tokens are driven by a \emph{common} matrix-valued Brownian noise. In this limit, we show that initialization noise prevents the collapse to a single cluster predicted by deterministic models. For two tokens, we prove a phase transition governed by the interaction strength and the token dimension: unlike deterministic attention flows, antipodal configurations become attracting with positive probability. Numerical experiments confirm the predicted transition, reveal that antipodal formations persist for more than two tokens, and demonstrate that suppressing the intrinsic noise degrades accuracy.

Control Variate Score Matching for Diffusion Models

Diffusion models offer a robust framework for sampling from unnormalized probability densities, which requires accurately estimating the score of the noise-perturbed target distribution. While the standard Denoising Score Identity (DSI) relies on data samples, access to the target energy function enables an alternative formulation via the Target Score Identity (TSI). However, these estimators face a fundamental variance trade-off: DSI exhibits high variance in low-noise regimes, whereas TSI suffers from high variance at high noise levels. In this work, we reconcile these approaches by unifying both estimators within the principled framework of control variates. We introduce the Control Variate Score Identity (CVSI), deriving an optimal, time-dependent control coefficient that theoretically guarantees variance minimization across the entire noise spectrum. We demonstrate that CVSI serves as a robust, low-variance plug-in estimator that significantly enhances sample efficiency in both data-free sampler learning and inference-time diffusion sampling.

Language Agents as Digital Representatives in Collective Decision-Making

Consider the process of collective decision-making, in which a group of individuals interactively select a preferred outcome from among a universe of alternatives. In this context, "representation" is the activity of making an individual's preferences present in the process via participation by a proxy agent -- i.e. their "representative". To this end, learned models of human behavior have the potential to fill this role, with practical implications for multi-agent scenario studies and mechanism design. In this work, we investigate the possibility of training \textit{language agents} to behave in the capacity of representatives of human agents, appropriately expressing the preferences of those individuals whom they stand for. First, we formalize the setting of \textit{collective decision-making} -- as the episodic process of interaction between a group of agents and a decision mechanism. On this basis, we then formalize the problem of \textit{digital representation} -- as the simulation of an agent's behavior to yield equivalent outcomes from the mechanism. Finally, we conduct an empirical case study in the setting of \textit{consensus-finding} among diverse humans, and demonstrate the feasibility of fine-tuning large language models to act as digital representatives.

Diversity-Rewarded CFG Distillation

Generative models are transforming creative domains such as music generation, with inference-time strategies like Classifier-Free Guidance (CFG) playing a crucial role. However, CFG doubles inference cost while limiting originality and diversity across generated contents. In this paper, we introduce diversity-rewarded CFG distillation, a novel finetuning procedure that distills the strengths of CFG while addressing its limitations. Our approach optimises two training objectives: (1) a distillation objective, encouraging the model alone (without CFG) to imitate the CFG-augmented predictions, and (2) an RL objective with a diversity reward, promoting the generation of diverse outputs for a given prompt. By finetuning, we learn model weights with the ability to generate high-quality and diverse outputs, without any inference overhead. This also unlocks the potential of weight-based model merging strategies: by interpolating between the weights of two models (the first focusing on quality, the second on diversity), we can control the quality-diversity trade-off at deployment time, and even further boost performance. We conduct extensive experiments on the MusicLM (Agostinelli et al., 2023) text-to-music generative model, where our approach surpasses CFG in terms of quality-diversity Pareto optimality. According to human evaluators, our finetuned-then-merged model generates samples with higher quality-diversity than the base model augmented with CFG. Explore our generations at https://google-research.github.io/seanet/musiclm/diverse_music/.

Using deep reinforcement learning to promote sustainable human behaviour on a common pool resource problem

A canonical social dilemma arises when finite resources are allocated to a group of people, who can choose to either reciprocate with interest, or keep the proceeds for themselves. What resource allocation mechanisms will encourage levels of reciprocation that sustain the commons? Here, in an iterated multiplayer trust game, we use deep reinforcement learning (RL) to design an allocation mechanism that endogenously promotes sustainable contributions from human participants to a common pool resource. We first trained neural networks to behave like human players, creating a stimulated economy that allowed us to study how different mechanisms influenced the dynamics of receipt and reciprocation. We then used RL to train a social planner to maximise aggregate return to players. The social planner discovered a redistributive policy that led to a large surplus and an inclusive economy, in which players made roughly equal gains. The RL agent increased human surplus over baseline mechanisms based on unrestricted welfare or conditional cooperation, by conditioning its generosity on available resources and temporarily sanctioning defectors by allocating fewer resources to them. Examining the AI policy allowed us to develop an explainable mechanism that performed similarly and was more popular among players. Deep reinforcement learning can be used to discover mechanisms that promote sustainable human behaviour.

TacticAI: an AI assistant for football tactics

Identifying key patterns of tactics implemented by rival teams, and developing effective responses, lies at the heart of modern football. However, doing so algorithmically remains an open research challenge. To address this unmet need, we propose TacticAI, an AI football tactics assistant developed and evaluated in close collaboration with domain experts from Liverpool FC. We focus on analysing corner kicks, as they offer coaches the most direct opportunities for interventions and improvements. TacticAI incorporates both a predictive and a generative component, allowing the coaches to effectively sample and explore alternative player setups for each corner kick routine and to select those with the highest predicted likelihood of success. We validate TacticAI on a number of relevant benchmark tasks: predicting receivers and shot attempts and recommending player position adjustments. The utility of TacticAI is validated by a qualitative study conducted with football domain experts at Liverpool FC. We show that TacticAI's model suggestions are not only indistinguishable from real tactics, but also favoured over existing tactics 90% of the time, and that TacticAI offers an effective corner kick retrieval system. TacticAI achieves these results despite the limited availability of gold-standard data, achieving data efficiency through geometric deep learning.

Developing, Evaluating and Scaling Learning Agents in Multi-Agent Environments

The Game Theory & Multi-Agent team at DeepMind studies several aspects of multi-agent learning ranging from computing approximations to fundamental concepts in game theory to simulating social dilemmas in rich spatial environments and training 3-d humanoids in difficult team coordination tasks. A signature aim of our group is to use the resources and expertise made available to us at DeepMind in deep reinforcement learning to explore multi-agent systems in complex environments and use these benchmarks to advance our understanding. Here, we summarise the recent work of our team and present a taxonomy that we feel highlights many important open challenges in multi-agent research.

Learning Correlated Equilibria in Mean-Field Games

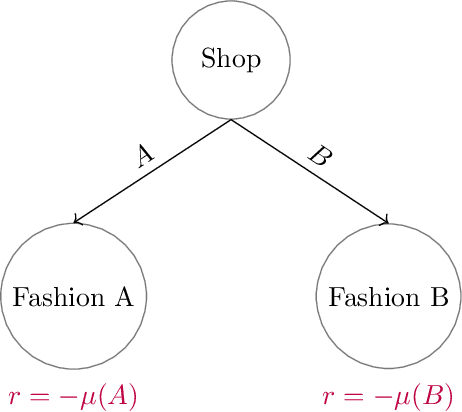
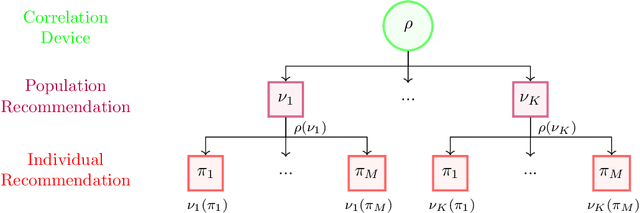
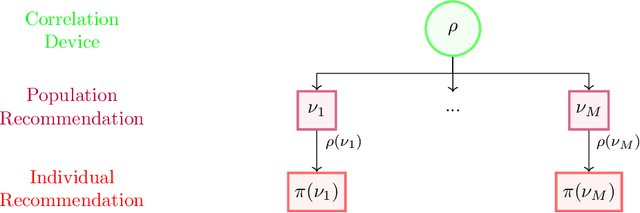
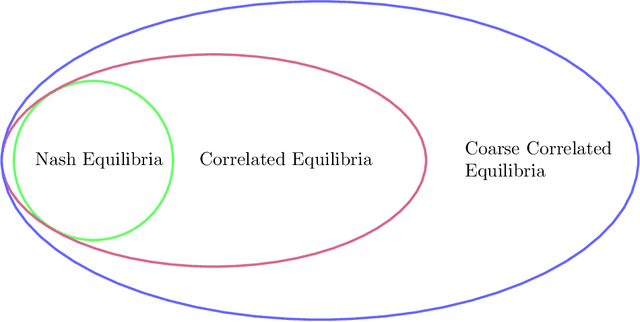
The designs of many large-scale systems today, from traffic routing environments to smart grids, rely on game-theoretic equilibrium concepts. However, as the size of an $N$-player game typically grows exponentially with $N$, standard game theoretic analysis becomes effectively infeasible beyond a low number of players. Recent approaches have gone around this limitation by instead considering Mean-Field games, an approximation of anonymous $N$-player games, where the number of players is infinite and the population's state distribution, instead of every individual player's state, is the object of interest. The practical computability of Mean-Field Nash equilibria, the most studied Mean-Field equilibrium to date, however, typically depends on beneficial non-generic structural properties such as monotonicity or contraction properties, which are required for known algorithms to converge. In this work, we provide an alternative route for studying Mean-Field games, by developing the concepts of Mean-Field correlated and coarse-correlated equilibria. We show that they can be efficiently learnt in \emph{all games}, without requiring any additional assumption on the structure of the game, using three classical algorithms. Furthermore, we establish correspondences between our notions and those already present in the literature, derive optimality bounds for the Mean-Field - $N$-player transition, and empirically demonstrate the convergence of these algorithms on simple games.

Mastering the Game of Stratego with Model-Free Multiagent Reinforcement Learning

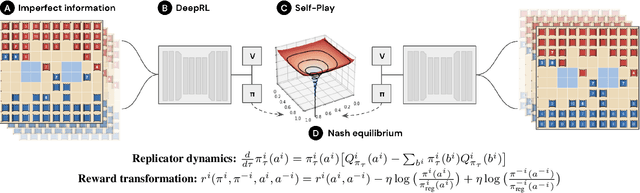
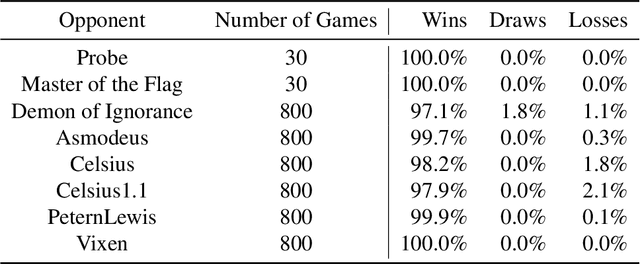
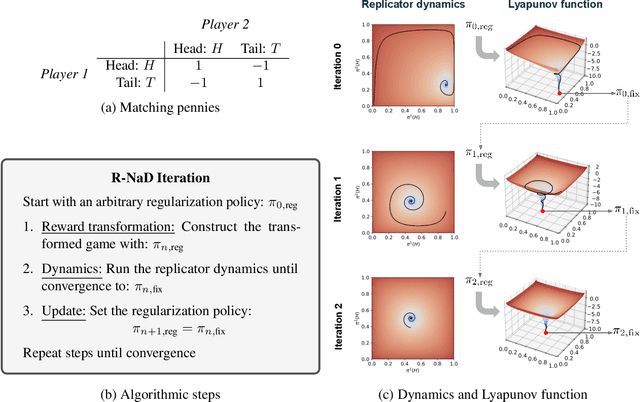
We introduce DeepNash, an autonomous agent capable of learning to play the imperfect information game Stratego from scratch, up to a human expert level. Stratego is one of the few iconic board games that Artificial Intelligence (AI) has not yet mastered. This popular game has an enormous game tree on the order of $10^{535}$ nodes, i.e., $10^{175}$ times larger than that of Go. It has the additional complexity of requiring decision-making under imperfect information, similar to Texas hold'em poker, which has a significantly smaller game tree (on the order of $10^{164}$ nodes). Decisions in Stratego are made over a large number of discrete actions with no obvious link between action and outcome. Episodes are long, with often hundreds of moves before a player wins, and situations in Stratego can not easily be broken down into manageably-sized sub-problems as in poker. For these reasons, Stratego has been a grand challenge for the field of AI for decades, and existing AI methods barely reach an amateur level of play. DeepNash uses a game-theoretic, model-free deep reinforcement learning method, without search, that learns to master Stratego via self-play. The Regularised Nash Dynamics (R-NaD) algorithm, a key component of DeepNash, converges to an approximate Nash equilibrium, instead of 'cycling' around it, by directly modifying the underlying multi-agent learning dynamics. DeepNash beats existing state-of-the-art AI methods in Stratego and achieved a yearly (2022) and all-time top-3 rank on the Gravon games platform, competing with human expert players.

An overview of active learning methods for insurance with fairness appreciation

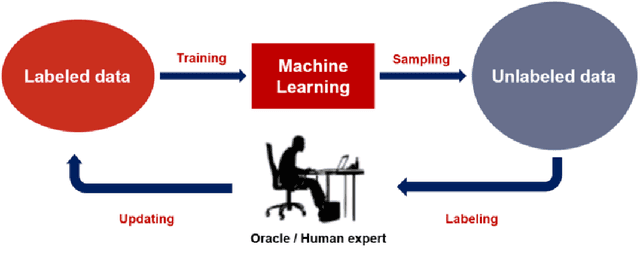
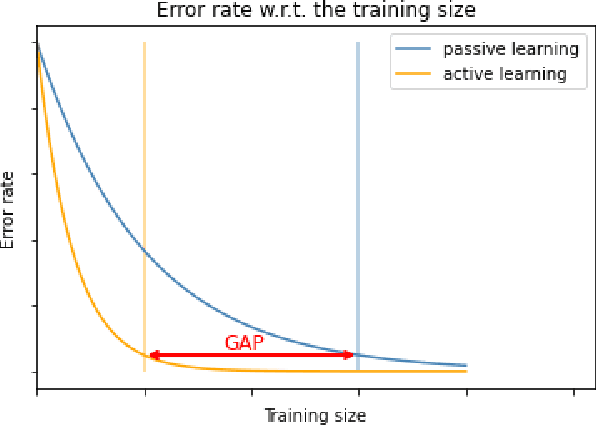
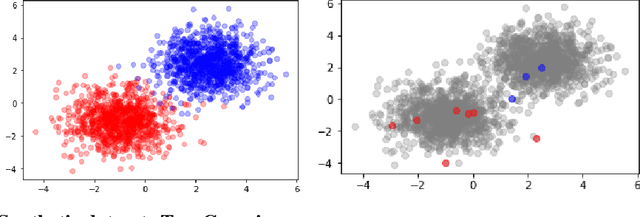
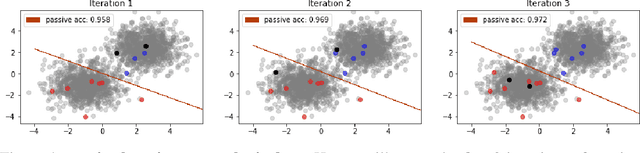
This paper addresses and solves some challenges in the adoption of machine learning in insurance with the democratization of model deployment. The first challenge is reducing the labelling effort (hence focusing on the data quality) with the help of active learning, a feedback loop between the model inference and an oracle: as in insurance the unlabeled data is usually abundant, active learning can become a significant asset in reducing the labelling cost. For that purpose, this paper sketches out various classical active learning methodologies before studying their empirical impact on both synthetic and real datasets. Another key challenge in insurance is the fairness issue in model inferences. We will introduce and integrate a post-processing fairness for multi-class tasks in this active learning framework to solve these two issues. Finally numerical experiments on unfair datasets highlight that the proposed setup presents a good compromise between model precision and fairness.