Code World Models for General Game Playing

Large Language Models (LLMs) reasoning abilities are increasingly being applied to classical board and card games, but the dominant approach -- involving prompting for direct move generation -- has significant drawbacks. It relies on the model's implicit fragile pattern-matching capabilities, leading to frequent illegal moves and strategically shallow play. Here we introduce an alternative approach: We use the LLM to translate natural language rules and game trajectories into a formal, executable world model represented as Python code. This generated model -- comprising functions for state transition, legal move enumeration, and termination checks -- serves as a verifiable simulation engine for high-performance planning algorithms like Monte Carlo tree search (MCTS). In addition, we prompt the LLM to generate heuristic value functions (to make MCTS more efficient), and inference functions (to estimate hidden states in imperfect information games). Our method offers three distinct advantages compared to directly using the LLM as a policy: (1) Verifiability: The generated CWM serves as a formal specification of the game's rules, allowing planners to algorithmically enumerate valid actions and avoid illegal moves, contingent on the correctness of the synthesized model; (2) Strategic Depth: We combine LLM semantic understanding with the deep search power of classical planners; and (3) Generalization: We direct the LLM to focus on the meta-task of data-to-code translation, enabling it to adapt to new games more easily. We evaluate our agent on 10 different games, of which 4 are novel and created for this paper. 5 of the games are fully observed (perfect information), and 5 are partially observed (imperfect information). We find that our method outperforms or matches Gemini 2.5 Pro in 9 out of the 10 considered games.

Re-evaluating Open-ended Evaluation of Large Language Models

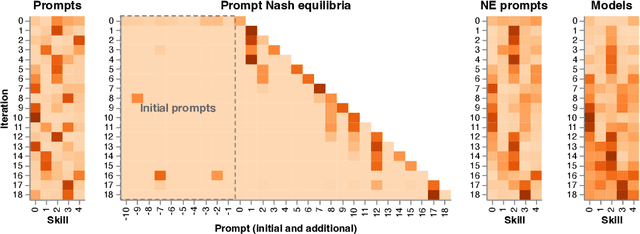
Evaluation has traditionally focused on ranking candidates for a specific skill. Modern generalist models, such as Large Language Models (LLMs), decidedly outpace this paradigm. Open-ended evaluation systems, where candidate models are compared on user-submitted prompts, have emerged as a popular solution. Despite their many advantages, we show that the current Elo-based rating systems can be susceptible to and even reinforce biases in data, intentional or accidental, due to their sensitivity to redundancies. To address this issue, we propose evaluation as a 3-player game, and introduce novel game-theoretic solution concepts to ensure robustness to redundancy. We show that our method leads to intuitive ratings and provide insights into the competitive landscape of LLM development.

Deviation Ratings: A General, Clone-Invariant Rating Method

Many real-world multi-agent or multi-task evaluation scenarios can be naturally modelled as normal-form games due to inherent strategic (adversarial, cooperative, and mixed motive) interactions. These strategic interactions may be agentic (e.g. players trying to win), fundamental (e.g. cost vs quality), or complementary (e.g. niche finding and specialization). In such a formulation, it is the strategies (actions, policies, agents, models, tasks, prompts, etc.) that are rated. However, the rating problem is complicated by redundancy and complexity of N-player strategic interactions. Repeated or similar strategies can distort ratings for those that counter or complement them. Previous work proposed ``clone invariant'' ratings to handle such redundancies, but this was limited to two-player zero-sum (i.e. strictly competitive) interactions. This work introduces the first N-player general-sum clone invariant rating, called deviation ratings, based on coarse correlated equilibria. The rating is explored on several domains including LLMs evaluation.

Jackpot! Alignment as a Maximal Lottery

Reinforcement Learning from Human Feedback (RLHF), the standard for aligning Large Language Models (LLMs) with human values, is known to fail to satisfy properties that are intuitively desirable, such as respecting the preferences of the majority \cite{ge2024axioms}. To overcome these issues, we propose the use of a probabilistic Social Choice rule called \emph{maximal lotteries} as a replacement for RLHF. We show that a family of alignment techniques, namely Nash Learning from Human Feedback (NLHF) \cite{munos2023nash} and variants, approximate maximal lottery outcomes and thus inherit its beneficial properties. We confirm experimentally that our proposed methodology handles situations that arise when working with preferences more robustly than standard RLHF, including supporting the preferences of the majority, providing principled ways of handling non-transitivities in the preference data, and robustness to irrelevant alternatives. This results in systems that better incorporate human values and respect human intentions.

Soft Condorcet Optimization for Ranking of General Agents

A common way to drive progress of AI models and agents is to compare their performance on standardized benchmarks. Comparing the performance of general agents requires aggregating their individual performances across a potentially wide variety of different tasks. In this paper, we describe a novel ranking scheme inspired by social choice frameworks, called Soft Condorcet Optimization (SCO), to compute the optimal ranking of agents: the one that makes the fewest mistakes in predicting the agent comparisons in the evaluation data. This optimal ranking is the maximum likelihood estimate when evaluation data (which we view as votes) are interpreted as noisy samples from a ground truth ranking, a solution to Condorcet's original voting system criteria. SCO ratings are maximal for Condorcet winners when they exist, which we show is not necessarily true for the classical rating system Elo. We propose three optimization algorithms to compute SCO ratings and evaluate their empirical performance. When serving as an approximation to the Kemeny-Young voting method, SCO rankings are on average 0 to 0.043 away from the optimal ranking in normalized Kendall-tau distance across 865 preference profiles from the PrefLib open ranking archive. In a simulated noisy tournament setting, SCO achieves accurate approximations to the ground truth ranking and the best among several baselines when 59\% or more of the preference data is missing. Finally, SCO ranking provides the best approximation to the optimal ranking, measured on held-out test sets, in a problem containing 52,958 human players across 31,049 games of the classic seven-player game of Diplomacy.

Easy as ABCs: Unifying Boltzmann Q-Learning and Counterfactual Regret Minimization

We propose ABCs (Adaptive Branching through Child stationarity), a best-of-both-worlds algorithm combining Boltzmann Q-learning (BQL), a classic reinforcement learning algorithm for single-agent domains, and counterfactual regret minimization (CFR), a central algorithm for learning in multi-agent domains. ABCs adaptively chooses what fraction of the environment to explore each iteration by measuring the stationarity of the environment's reward and transition dynamics. In Markov decision processes, ABCs converges to the optimal policy with at most an O(A) factor slowdown compared to BQL, where A is the number of actions in the environment. In two-player zero-sum games, ABCs is guaranteed to converge to a Nash equilibrium (assuming access to a perfect oracle for detecting stationarity), while BQL has no such guarantees. Empirically, ABCs demonstrates strong performance when benchmarked across environments drawn from the OpenSpiel game library and OpenAI Gym and exceeds all prior methods in environments which are neither fully stationary nor fully nonstationary.

States as Strings as Strategies: Steering Language Models with Game-Theoretic Solvers

Game theory is the study of mathematical models of strategic interactions among rational agents. Language is a key medium of interaction for humans, though it has historically proven difficult to model dialogue and its strategic motivations mathematically. A suitable model of the players, strategies, and payoffs associated with linguistic interactions (i.e., a binding to the conventional symbolic logic of game theory) would enable existing game-theoretic algorithms to provide strategic solutions in the space of language. In other words, a binding could provide a route to computing stable, rational conversational strategies in dialogue. Large language models (LLMs) have arguably reached a point where their generative capabilities can enable realistic, human-like simulations of natural dialogue. By prompting them in various ways, we can steer their responses towards different output utterances. Leveraging the expressivity of natural language, LLMs can also help us quickly generate new dialogue scenarios, which are grounded in real world applications. In this work, we present one possible binding from dialogue to game theory as well as generalizations of existing equilibrium finding algorithms to this setting. In addition, by exploiting LLMs generation capabilities along with our proposed binding, we can synthesize a large repository of formally-defined games in which one can study and test game-theoretic solution concepts. We also demonstrate how one can combine LLM-driven game generation, game-theoretic solvers, and imitation learning to construct a process for improving the strategic capabilities of LLMs.

Neural Population Learning beyond Symmetric Zero-sum Games

We study computationally efficient methods for finding equilibria in n-player general-sum games, specifically ones that afford complex visuomotor skills. We show how existing methods would struggle in this setting, either computationally or in theory. We then introduce NeuPL-JPSRO, a neural population learning algorithm that benefits from transfer learning of skills and converges to a Coarse Correlated Equilibrium (CCE) of the game. We show empirical convergence in a suite of OpenSpiel games, validated rigorously by exact game solvers. We then deploy NeuPL-JPSRO to complex domains, where our approach enables adaptive coordination in a MuJoCo control domain and skill transfer in capture-the-flag. Our work shows that equilibrium convergent population learning can be implemented at scale and in generality, paving the way towards solving real-world games between heterogeneous players with mixed motives.

Evaluating Agents using Social Choice Theory

We argue that many general evaluation problems can be viewed through the lens of voting theory. Each task is interpreted as a separate voter, which requires only ordinal rankings or pairwise comparisons of agents to produce an overall evaluation. By viewing the aggregator as a social welfare function, we are able to leverage centuries of research in social choice theory to derive principled evaluation frameworks with axiomatic foundations. These evaluations are interpretable and flexible, while avoiding many of the problems currently facing cross-task evaluation. We apply this Voting-as-Evaluation (VasE) framework across multiple settings, including reinforcement learning, large language models, and humans. In practice, we observe that VasE can be more robust than popular evaluation frameworks (Elo and Nash averaging), discovers properties in the evaluation data not evident from scores alone, and can predict outcomes better than Elo in a complex seven-player game. We identify one particular approach, maximal lotteries, that satisfies important consistency properties relevant to evaluation, is computationally efficient (polynomial in the size of the evaluation data), and identifies game-theoretic cycles.

Learning not to Regret

Regret minimization is a key component of many algorithms for finding Nash equilibria in imperfect-information games. To scale to games that cannot fit in memory, we can use search with value functions. However, calling the value functions repeatedly in search can be expensive. Therefore, it is desirable to minimize regret in the search tree as fast as possible. We propose to accelerate the regret minimization by introducing a general ``learning not to regret'' framework, where we meta-learn the regret minimizer. The resulting algorithm is guaranteed to minimize regret in arbitrary settings and is (meta)-learned to converge fast on a selected distribution of games. Our experiments show that meta-learned algorithms converge substantially faster than prior regret minimization algorithms.