Massively Parallel Proof-Number Search for Impartial Games and Beyond

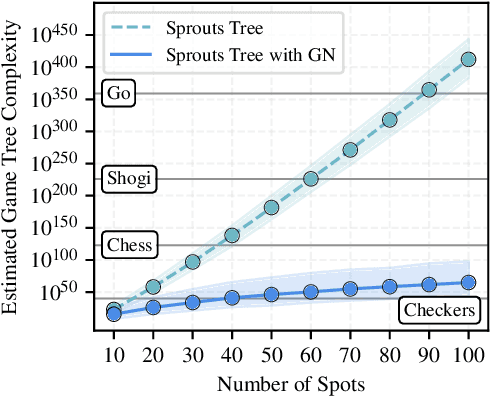
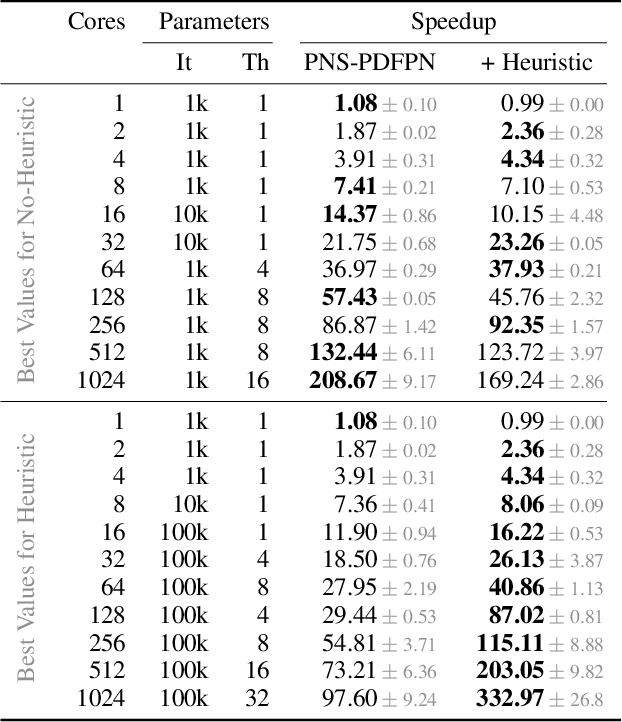
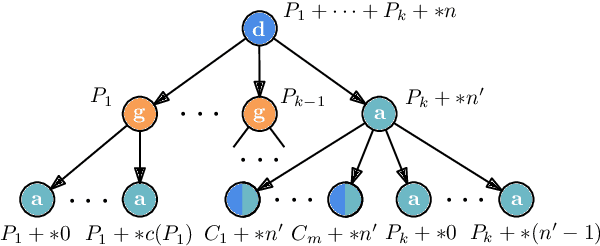
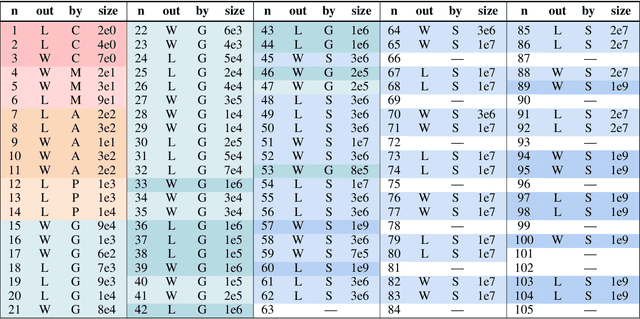
Proof-Number Search is a best-first search algorithm with many successful applications, especially in game solving. As large-scale computing clusters become increasingly accessible, parallelization is a natural way to accelerate computation. However, existing parallel versions of Proof-Number Search are known to scale poorly on many CPU cores. Using two parallelized levels and shared information among workers, we present the first massively parallel version of Proof-Number Search that scales efficiently even on a large number of CPUs. We apply our solver, enhanced with Grundy numbers for reducing game trees, to the Sprouts game, a case study motivated by the long-standing Sprouts Conjecture. Our solver achieves a significantly improved 332.9$\times$ speedup when run on 1024 cores, enabling it to outperform the state-of-the-art Sprouts solver GLOP by four orders of magnitude in runtime and to generate proofs 1,000$\times$ more complex. Despite exponential growth in game tree size, our solver verified the Sprouts Conjecture for 42 new positions, nearly doubling the number of known outcomes.

Artificial Generals Intelligence: Mastering Generals.io with Reinforcement Learning

We introduce a real-time strategy game environment built on Generals.io, a game that hosts thousands of active players each week across multiple game formats. Our environment is fully compatible with Gymnasium and PettingZoo, capable of running thousands of frames per second on commodity hardware. Our reference agent -- trained with supervised pre-training and self-play -- hits the top 0.003\% of the 1v1 human leaderboard after just 36 hours on a single H100 GPU. To accelerate learning, we incorporate potential-based reward shaping and memory features. Our contributions -- a modular RTS benchmark and a competitive, state-of-the-art baseline agent -- provide an accessible yet challenging platform for advancing multi-agent reinforcement learning research.

Meta-Learning in Self-Play Regret Minimization

Regret minimization is a general approach to online optimization which plays a crucial role in many algorithms for approximating Nash equilibria in two-player zero-sum games. The literature mainly focuses on solving individual games in isolation. However, in practice, players often encounter a distribution of similar but distinct games. For example, when trading correlated assets on the stock market, or when refining the strategy in subgames of a much larger game. Recently, offline meta-learning was used to accelerate one-sided equilibrium finding on such distributions. We build upon this, extending the framework to the more challenging self-play setting, which is the basis for most state-of-the-art equilibrium approximation algorithms for domains at scale. When selecting the strategy, our method uniquely integrates information across all decision states, promoting global communication as opposed to the traditional local regret decomposition. Empirical evaluation on normal-form games and river poker subgames shows our meta-learned algorithms considerably outperform other state-of-the-art regret minimization algorithms.

Learning to Beat ByteRL: Exploitability of Collectible Card Game Agents

While Poker, as a family of games, has been studied extensively in the last decades, collectible card games have seen relatively little attention. Only recently have we seen an agent that can compete with professional human players in Hearthstone, one of the most popular collectible card games. Although artificial agents must be able to work with imperfect information in both of these genres, collectible card games pose another set of distinct challenges. Unlike in many poker variants, agents must deal with state space so vast that even enumerating all states consistent with the agent's beliefs is intractable, rendering the current search methods unusable and requiring the agents to opt for other techniques. In this paper, we investigate the strength of such techniques for this class of games. Namely, we present preliminary analysis results of ByteRL, the state-of-the-art agent in Legends of Code and Magic and Hearthstone. Although ByteRL beat a top-10 Hearthstone player from China, we show that its play in Legends of Code and Magic is highly exploitable.

Learning not to Regret

Regret minimization is a key component of many algorithms for finding Nash equilibria in imperfect-information games. To scale to games that cannot fit in memory, we can use search with value functions. However, calling the value functions repeatedly in search can be expensive. Therefore, it is desirable to minimize regret in the search tree as fast as possible. We propose to accelerate the regret minimization by introducing a general ``learning not to regret'' framework, where we meta-learn the regret minimizer. The resulting algorithm is guaranteed to minimize regret in arbitrary settings and is (meta)-learned to converge fast on a selected distribution of games. Our experiments show that meta-learned algorithms converge substantially faster than prior regret minimization algorithms.

Player of Games

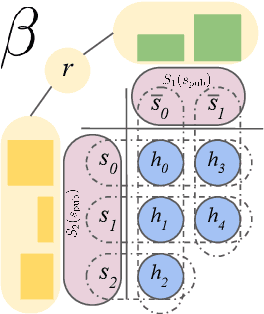
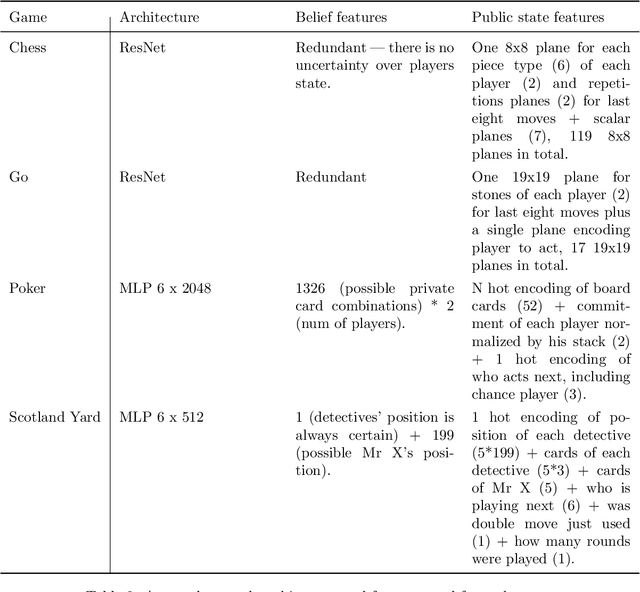
Games have a long history of serving as a benchmark for progress in artificial intelligence. Recently, approaches using search and learning have shown strong performance across a set of perfect information games, and approaches using game-theoretic reasoning and learning have shown strong performance for specific imperfect information poker variants. We introduce Player of Games, a general-purpose algorithm that unifies previous approaches, combining guided search, self-play learning, and game-theoretic reasoning. Player of Games is the first algorithm to achieve strong empirical performance in large perfect and imperfect information games -- an important step towards truly general algorithms for arbitrary environments. We prove that Player of Games is sound, converging to perfect play as available computation time and approximation capacity increases. Player of Games reaches strong performance in chess and Go, beats the strongest openly available agent in heads-up no-limit Texas hold'em poker (Slumbot), and defeats the state-of-the-art agent in Scotland Yard, an imperfect information game that illustrates the value of guided search, learning, and game-theoretic reasoning.

Search in Imperfect Information Games

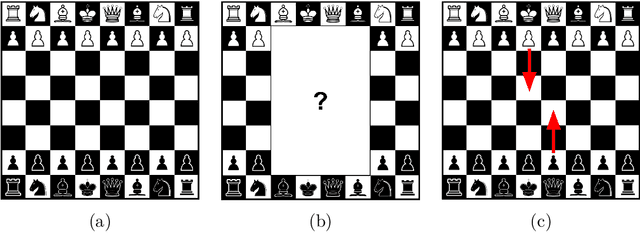
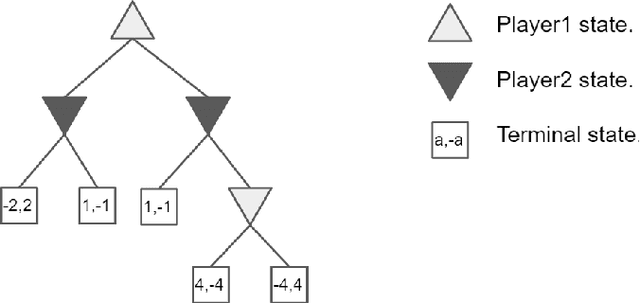
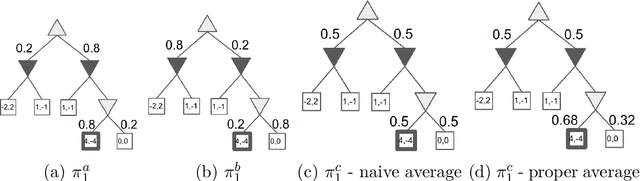
From the very dawn of the field, search with value functions was a fundamental concept of computer games research. Turing's chess algorithm from 1950 was able to think two moves ahead, and Shannon's work on chess from $1950$ includes an extensive section on evaluation functions to be used within a search. Samuel's checkers program from 1959 already combines search and value functions that are learned through self-play and bootstrapping. TD-Gammon improves upon those ideas and uses neural networks to learn those complex value functions -- only to be again used within search. The combination of decision-time search and value functions has been present in the remarkable milestones where computers bested their human counterparts in long standing challenging games -- DeepBlue for Chess and AlphaGo for Go. Until recently, this powerful framework of search aided with (learned) value functions has been limited to perfect information games. As many interesting problems do not provide the agent perfect information of the environment, this was an unfortunate limitation. This thesis introduces the reader to sound search for imperfect information games.

Solving Common-Payoff Games with Approximate Policy Iteration

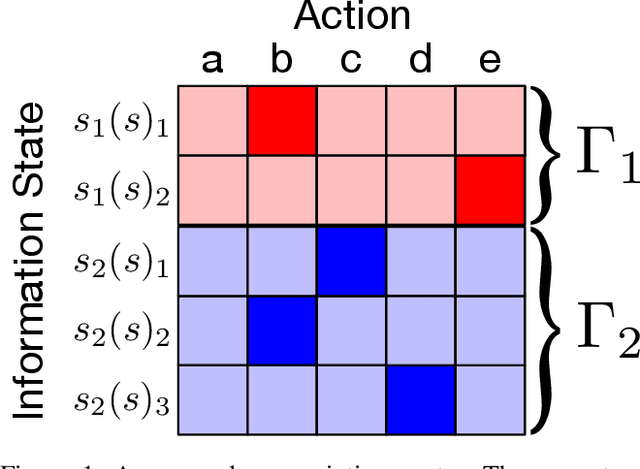
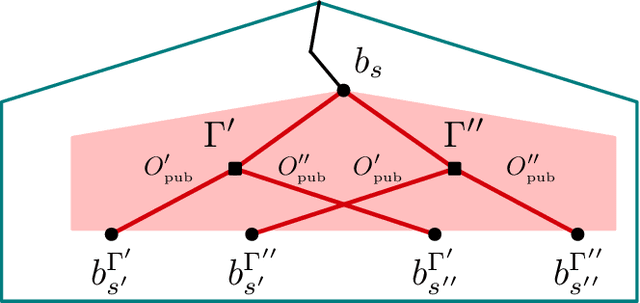
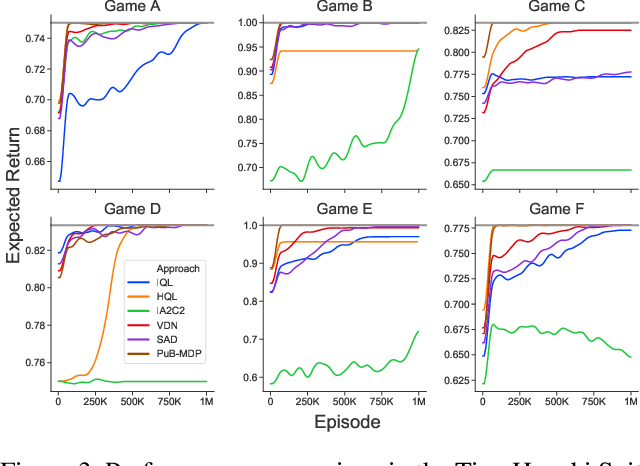
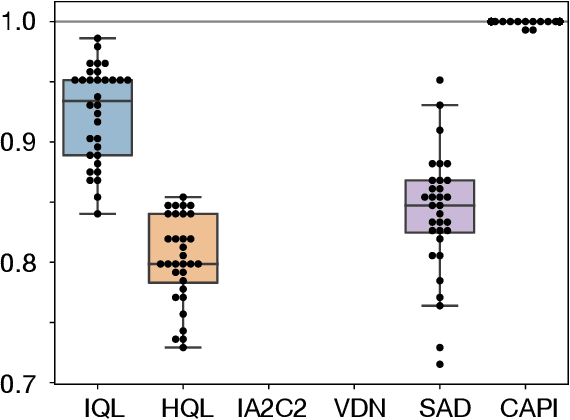
For artificially intelligent learning systems to have widespread applicability in real-world settings, it is important that they be able to operate decentrally. Unfortunately, decentralized control is difficult -- computing even an epsilon-optimal joint policy is a NEXP complete problem. Nevertheless, a recently rediscovered insight -- that a team of agents can coordinate via common knowledge -- has given rise to algorithms capable of finding optimal joint policies in small common-payoff games. The Bayesian action decoder (BAD) leverages this insight and deep reinforcement learning to scale to games as large as two-player Hanabi. However, the approximations it uses to do so prevent it from discovering optimal joint policies even in games small enough to brute force optimal solutions. This work proposes CAPI, a novel algorithm which, like BAD, combines common knowledge with deep reinforcement learning. However, unlike BAD, CAPI prioritizes the propensity to discover optimal joint policies over scalability. While this choice precludes CAPI from scaling to games as large as Hanabi, empirical results demonstrate that, on the games to which CAPI does scale, it is capable of discovering optimal joint policies even when other modern multi-agent reinforcement learning algorithms are unable to do so. Code is available at https://github.com/ssokota/capi .

The Advantage Regret-Matching Actor-Critic

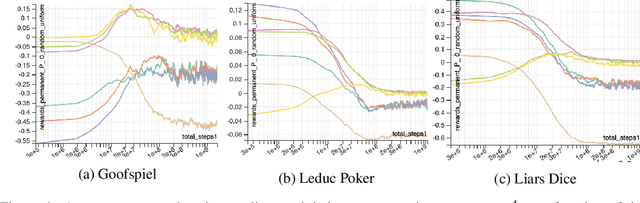
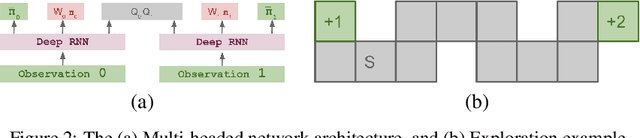
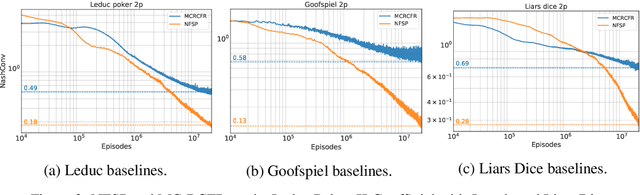
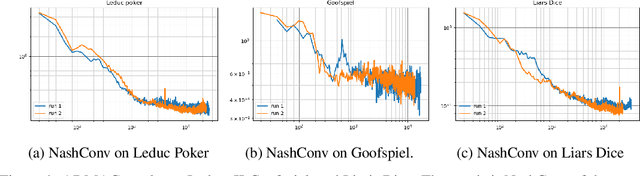
Regret minimization has played a key role in online learning, equilibrium computation in games, and reinforcement learning (RL). In this paper, we describe a general model-free RL method for no-regret learning based on repeated reconsideration of past behavior. We propose a model-free RL algorithm, the AdvantageRegret-Matching Actor-Critic (ARMAC): rather than saving past state-action data, ARMAC saves a buffer of past policies, replaying through them to reconstruct hindsight assessments of past behavior. These retrospective value estimates are used to predict conditional advantages which, combined with regret matching, produces a new policy. In particular, ARMAC learns from sampled trajectories in a centralized training setting, without requiring the application of importance sampling commonly used in Monte Carlo counterfactual regret (CFR) minimization; hence, it does not suffer from excessive variance in large environments. In the single-agent setting, ARMAC shows an interesting form of exploration by keeping past policies intact. In the multiagent setting, ARMAC in self-play approaches Nash equilibria on some partially-observable zero-sum benchmarks. We provide exploitability estimates in the significantly larger game of betting-abstracted no-limit Texas Hold'em.

Approximate exploitability: Learning a best response in large games

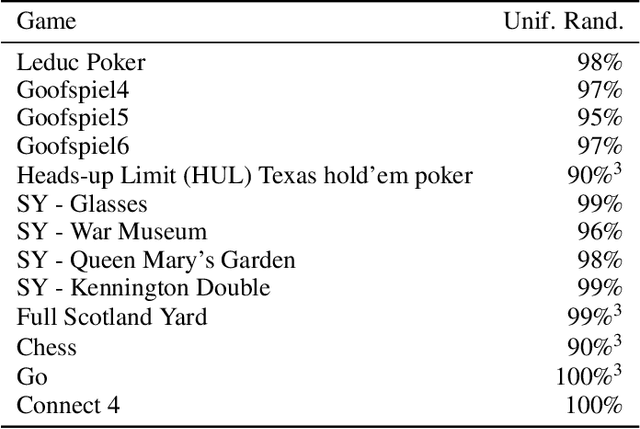
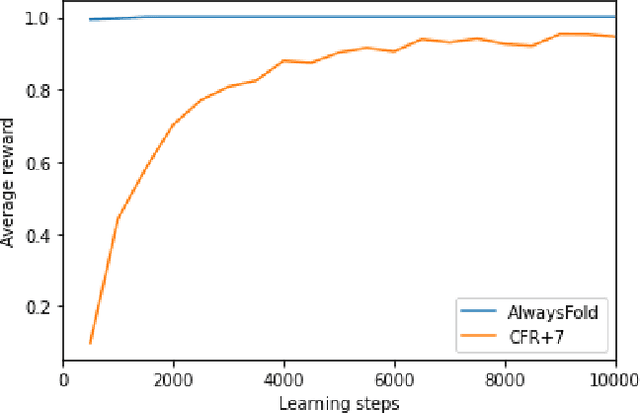
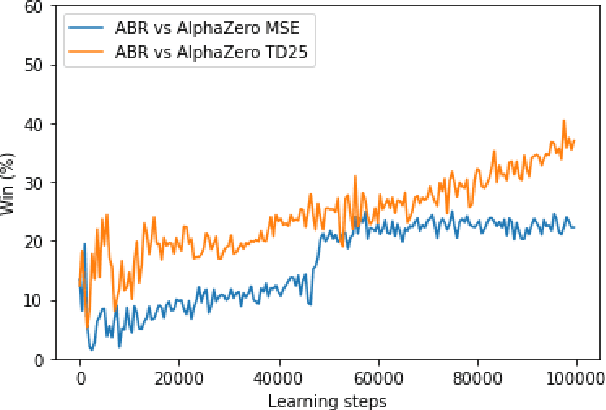
A common metric in games of imperfect information is exploitability, i.e. the performance of a policy against the worst-case opponent. This metric has many nice properties, but is intractable to compute in large games as it requires a full search of the game tree to calculate a best response to the given policy. We introduce a new metric, approximate exploitability, that calculates an analogous metric to exploitability using an approximate best response. This method scales to large games with tractable belief spaces. We focus only on the two-player, zero-sum case. Additionally, we provide empirical results for a specific instance of the method, demonstrating that it can effectively exploit agents in large games. We demonstrate that our method converges to exploitability in the tabular setting and the function approximation setting for small games, and demonstrate that it can consistently find exploits for weak policies in large games, showing results on Chess, Go, Heads-up No Limit Texas Hold'em, and other games.