BiConMP: A Nonlinear Model Predictive Control Framework for Whole Body Motion Planning

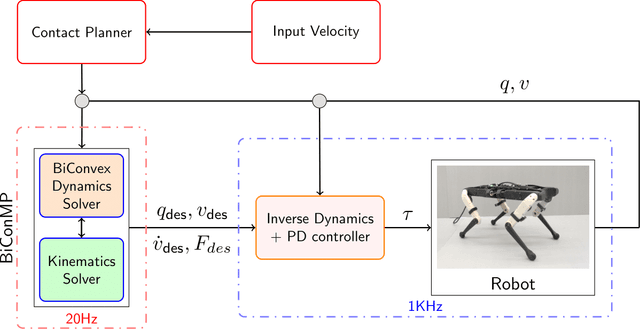
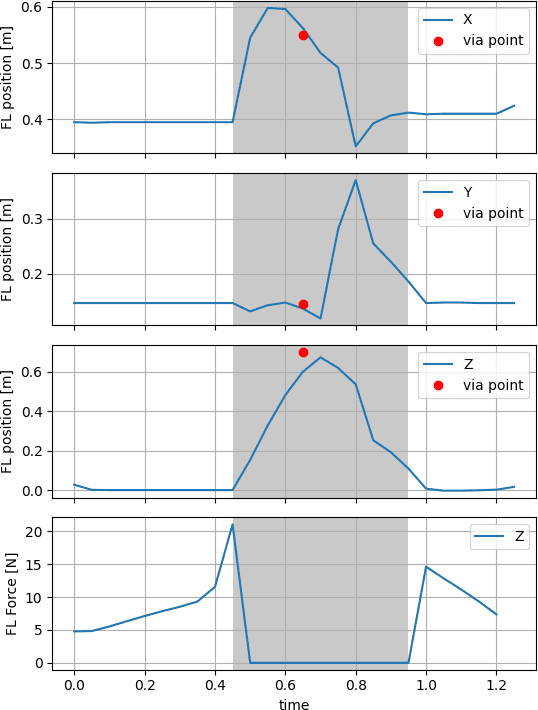
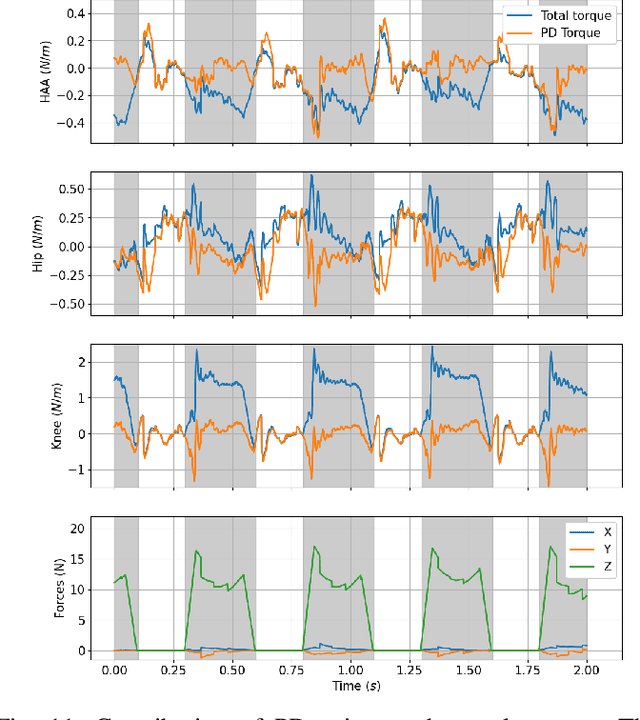
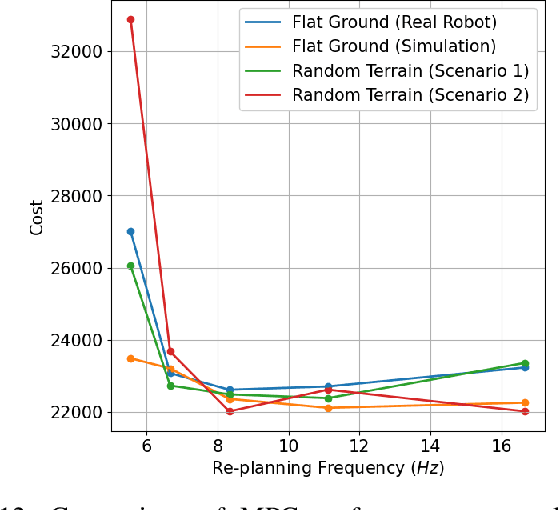
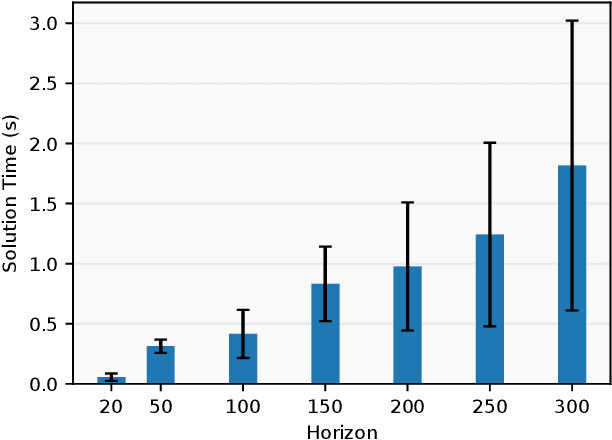
Online planning of whole-body motions for legged robots is challenging due to the inherent nonlinearity in the robot dynamics. In this work, we propose a nonlinear MPC framework, the BiConMP which can generate whole body trajectories online by efficiently exploiting the structure of the robot dynamics. BiConMP is used to generate various cyclic gaits on a real quadruped robot and its performance is evaluated on different terrain, countering unforeseen pushes and transitioning online between different gaits. Further, the ability of BiConMP to generate non-trivial acyclic whole-body dynamic motions on the robot is presented. Finally, an extensive empirical analysis on the effects of planning horizon and frequency on the nonlinear MPC framework is reported and discussed.

ValueNetQP: Learned one-step optimal control for legged locomotion

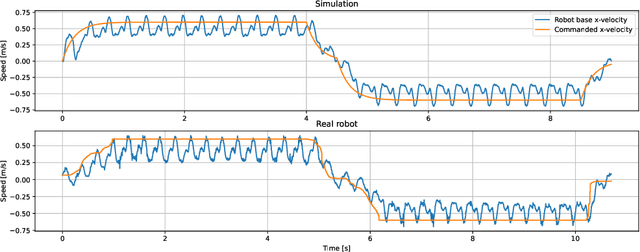
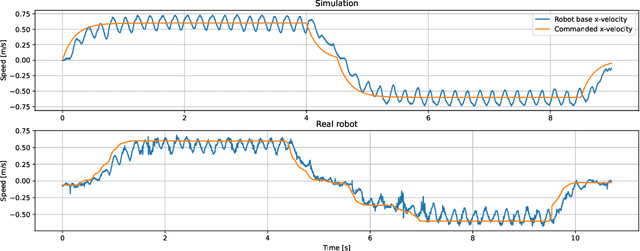
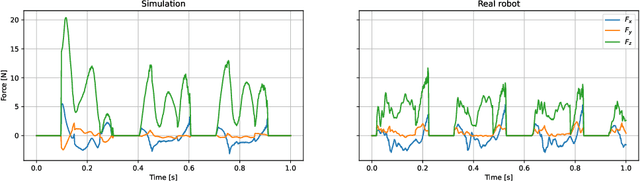
Optimal control is a successful approach to generate motions for complex robots, in particular for legged locomotion. However, these techniques are often too slow to run in real time for model predictive control or one needs to drastically simplify the dynamics model. In this work, we present a method to learn to predict the gradient and hessian of the problem value function, enabling fast resolution of the predictive control problem with a one-step quadratic program. In addition, our method is able to satisfy constraints like friction cones and unilateral constraints, which are important for high dynamics locomotion tasks. We demonstrate the capability of our method in simulation and on a real quadruped robot performing trotting and bounding motions.

Millimeter Wave Wireless Assisted Robot Navigation with Link State Classification

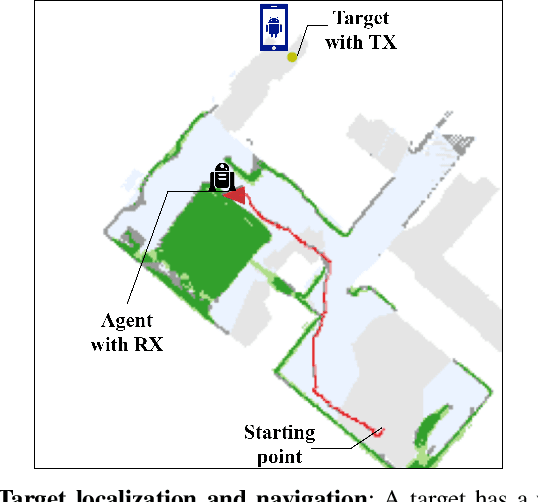
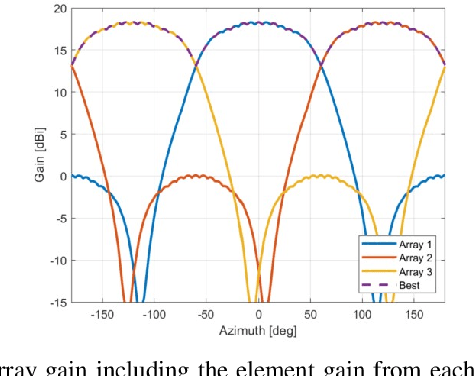
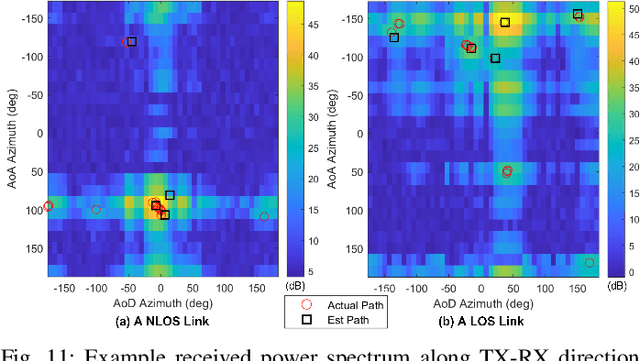
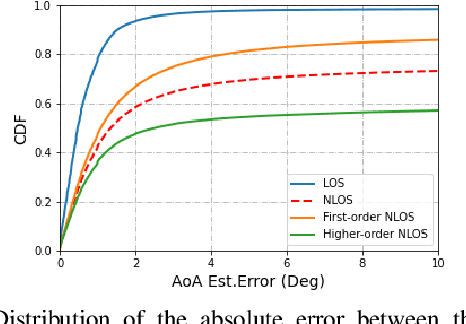
The millimeter wave (mmWave) bands have attracted considerable attention for high precision localization applications due to the ability to capture high angular and temporal resolution measurements. This paper explores mmWave-based positioning for a target localization problem where a fixed target broadcasts mmWave signals and a mobile robotic agent attempts to listen to the signals to locate and navigate to the target. A three strage procedure is proposed: First, the mobile agent uses tensor decomposition methods to detect the wireless paths and their angles. Second, a machine-learning trained classifier is then used to predict the link state, meaning if the strongest path is line-of-sight (LOS) or non-LOS (NLOS). For the NLOS case, the link state predictor also determines if the strongest path arrived via one or more reflections. Third, based on the link state, the agent either follows the estimated angles or explores the environment. The method is demonstrated on a large dataset of indoor environments supplemented with ray tracing to simulate the wireless propagation. The path estimation and link state classification are also integrated into a state-ofthe-art neural simultaneous localization and mapping (SLAM) module to augment camera and LIDAR-based navigation. It is shown that the link state classifier can successfully generalize to completely new environments outside the training set. In addition, the neural-SLAM module with the wireless path estimation and link state classifier provides rapid navigation to the target, close to a baseline that knows the target location.

A unified framework for walking and running of bipedal robots

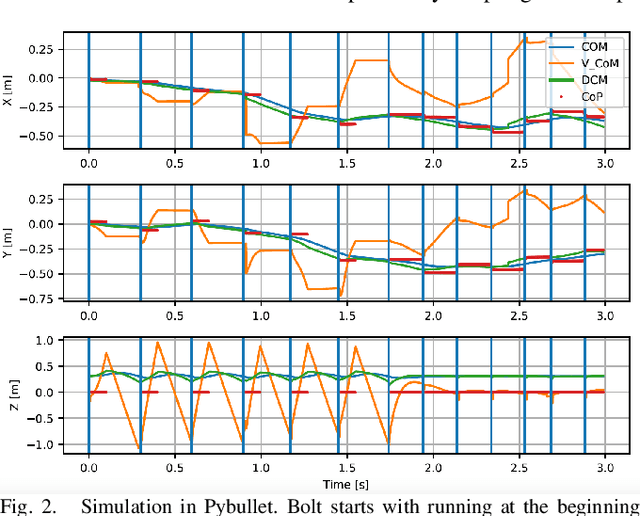
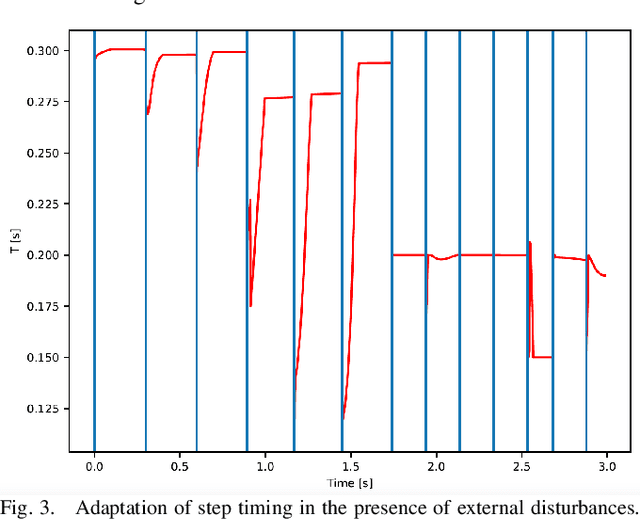
In this paper, we propose a novel framework capable of generating various walking and running gaits for bipedal robots. The main goal is to relax the fixed center of mass (CoM) height assumption of the linear inverted pendulum model (LIPM) and generate a wider range of walking and running motions, without a considerable increase in complexity. To do so, we use the concept of virtual constraints in the centroidal space which enables generating motions beyond walking while keeping the complexity at a minimum. By a proper choice of these virtual constraints, we show that we can generate different types of walking and running motions. More importantly, enforcing the virtual constraints through feedback renders the dynamics linear and enables us to design a feedback control mechanism which adapts the next step location and timing in face of disturbances, through a simple quadratic program (QP). To show the effectiveness of this framework, we showcase different walking and running simulations of the biped robot Bolt in the presence of both environmental uncertainties and external disturbances.

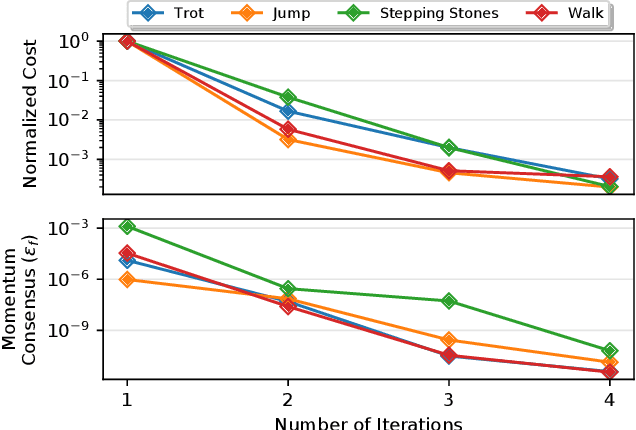
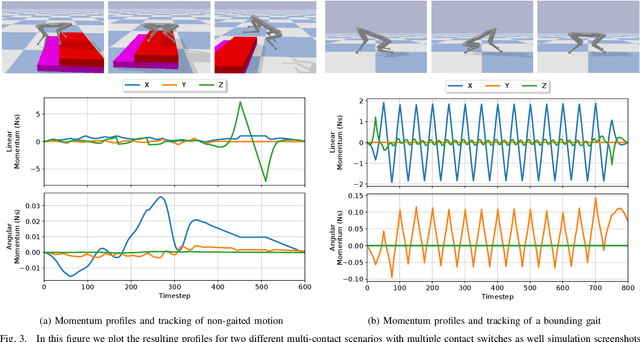
Rapid Convex Optimization of Centroidal Dynamics using Block Coordinate Descent

In this paper we explore the use of block coordinate descent (BCD) to optimize the centroidal momentum dynamics for dynamically consistent multi-contact behaviors. The centroidal dynamics have recently received a large amount of attention in order to create physically realizable motions for robots with hands and feet while being computationally more tractable than full rigid body dynamics models. Our contribution lies in exploiting the structure of the dynamics in order to simplify the original non-convex problem into two convex subproblems. We iterate between these two subproblems for a set number of iterations or until a consensus is reached. We explore the properties of the proposed optimization method for the centroidal dynamics and verify in simulation that motions generated by our approach can be tracked by the quadruped Solo12. In addition, we compare our method to a recently proposed convexification using a sequence of convex relaxations as well as a more standard interior point method used in the off- the-shelf solver IPOPT to show that our approach finds similar, if not better, trajectories (in terms of cost), and is more than four times faster than both approaches. Finally, compared to previous approaches, we note its practicality due to the convex nature of each subproblem which allows our method to be used with any off-the-shelf quadratic programming solver.

Model-free Reinforcement Learning for Robust Locomotion Using Trajectory Optimization for Exploration

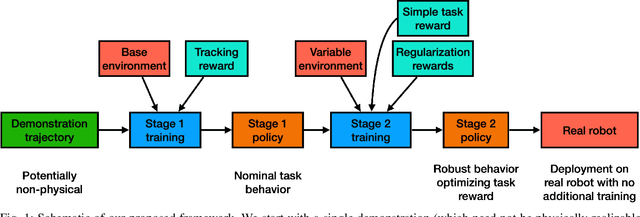
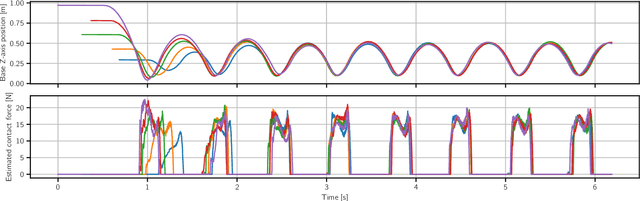
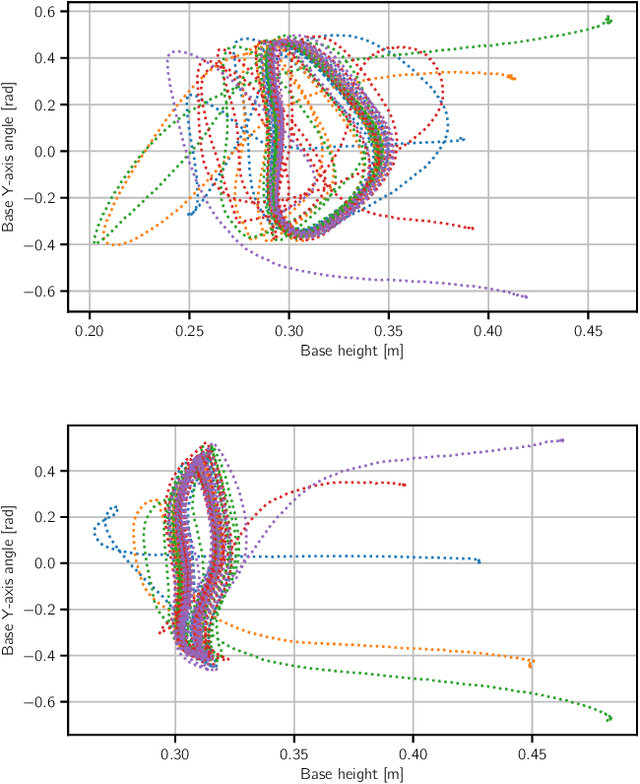
In this work we present a general, two-stage reinforcement learning approach for going from a single demonstration trajectory to a robust policy that can be deployed on hardware without any additional training. The demonstration is used in the first stage as a starting point to facilitate initial exploration. In the second stage, the relevant task reward is optimized directly and a policy robust to environment uncertainties is computed. We demonstrate and examine in detail performance and robustness of our approach on highly dynamic hopping and bounding tasks on a real quadruped robot.

$\mathcal{N}$IPM-HLSP: An Efficient Interior-Point Method for Hierarchical Least-Squares Programs

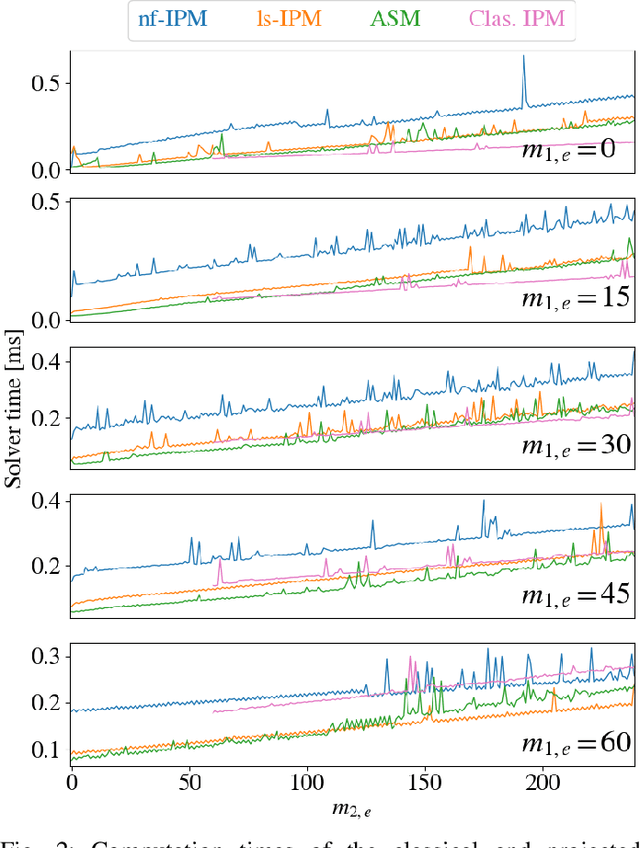
Hierarchical least-squares programs with linear constraints (HLSP) are a type of optimization problem very common in robotics. Each priority level contains an objective in least-squares form which is subject to the linear constraints of the higher priority hierarchy levels. Active-set methods (ASM) are a popular choice for solving them. However, they can perform poorly in terms of computational time if there are large changes of the active set. We therefore propose a computationally efficient primal-dual interior-point method (IPM) for HLSP's which is able to maintain constant numbers of solver iterations in these situations. We base our IPM on the null-space method which requires only a single decomposition per Newton iteration instead of two as it is the case for other IPM solvers. After a priority level has converged we compose a set of active constraints judging upon the dual and project lower priority levels into their null-space. We show that the IPM-HLSP can be expressed in least-squares form which avoids the formation of the quadratic Karush-Kuhn-Tucker (KKT) Hessian. Due to our choice of the null-space basis the IPM-HLSP is as fast as the state-of-the-art ASM-HLSP solver for equality only problems.

Learning Dynamical Systems from Noisy Sensor Measurements using Multiple Shooting

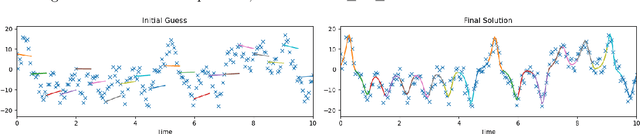
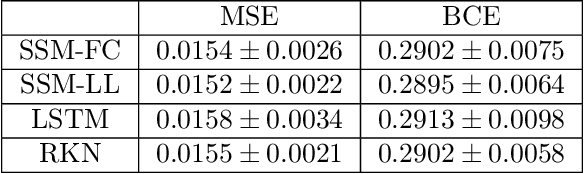
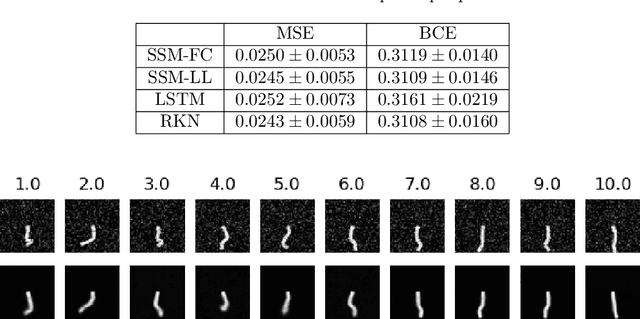
Modeling dynamical systems plays a crucial role in capturing and understanding complex physical phenomena. When physical models are not sufficiently accurate or hardly describable by analytical formulas, one can use generic function approximators such as neural networks to capture the system dynamics directly from sensor measurements. As for now, current methods to learn the parameters of these neural networks are highly sensitive to the inherent instability of most dynamical systems of interest, which in turn prevents the study of very long sequences. In this work, we introduce a generic and scalable method based on multiple shooting to learn latent representations of indirectly observed dynamical systems. We achieve state-of-the-art performances on systems observed directly from raw images. Further, we demonstrate that our method is robust to noisy measurements and can handle complex dynamical systems, such as chaotic ones.

A Robustness Analysis of Inverse Optimal Control of Bipedal Walking

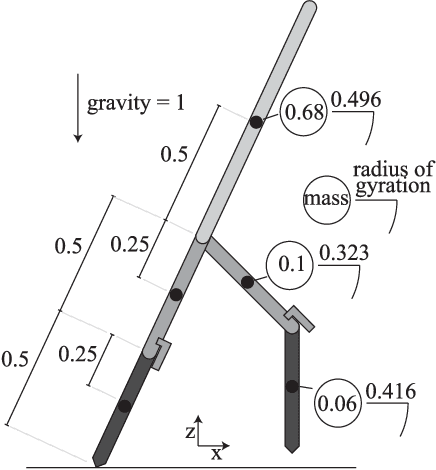
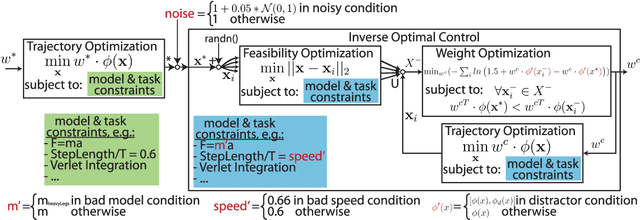
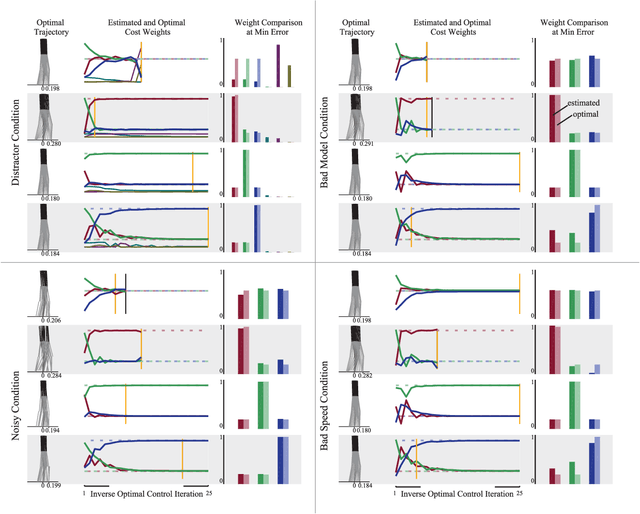
Cost functions have the potential to provide compact and understandable generalizations of motion. The goal of Inverse Optimal Control (IOC) is to analyze an observed behavior which is assumed to be optimal with respect to an unknown cost function, and infer this cost function. Here we develop a method for characterizing cost functions of legged locomotion, with the goal of representing complex humanoid behavior with simple models. To test this methodology we simulate walking gaits of a simple 5 link planar walking model which optimize known cost functions, and assess the ability of our IOC method to recover them. In particular, the IOC method uses an iterative trajectory optimization process to infer cost function weightings consistent with those used to generate a single demonstrated optimal trial. We also explore sensitivity of the IOC to sensor noise in the observed trajectory, imperfect knowledge of the model or task, as well as uncertainty in the components of the cost function used. With appropriate modeling, these methods may help infer cost functions from human data, yielding a compact and generalizable representation of human-like motion for use in humanoid robot controllers, as well as providing a new tool for experimentally exploring human preferences.

Simultaneous Navigation and Construction Benchmarking Environments

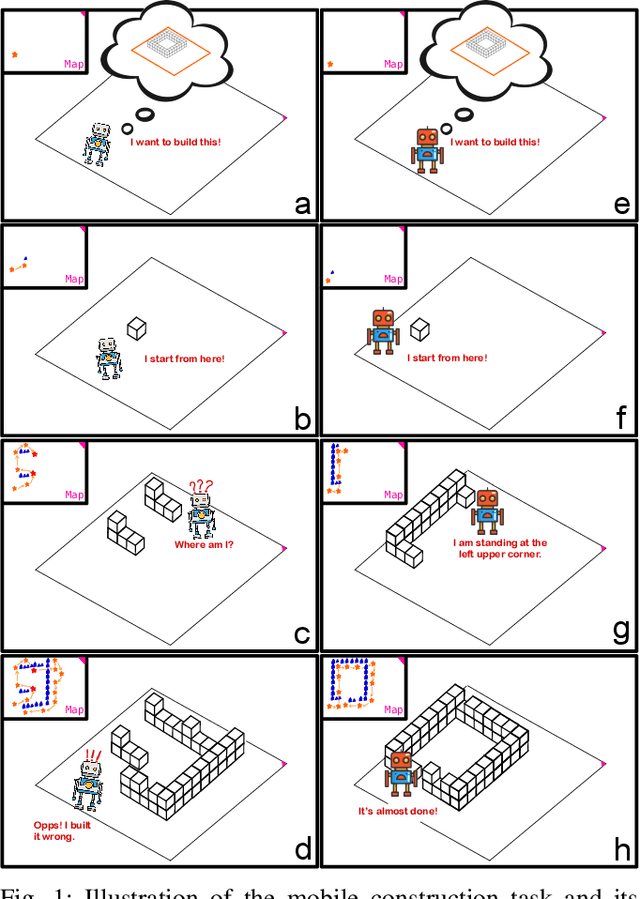
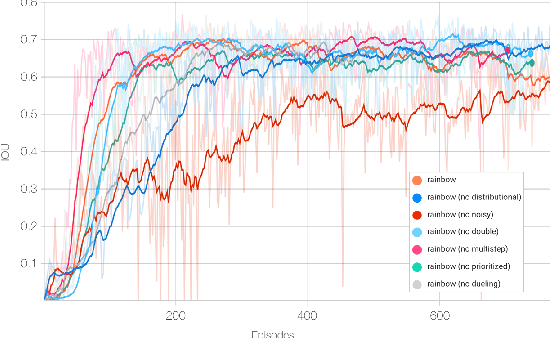
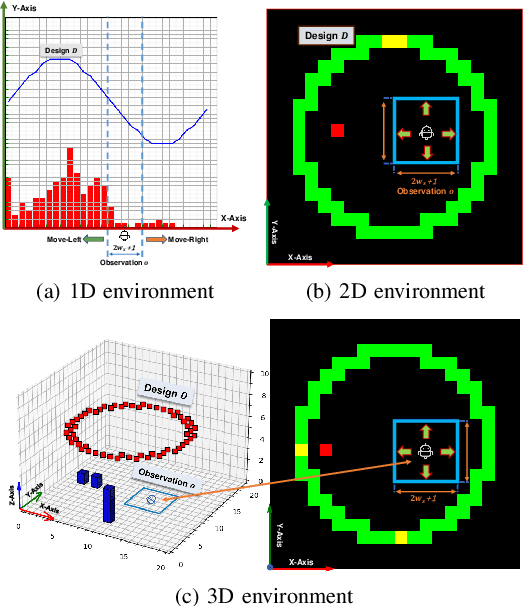
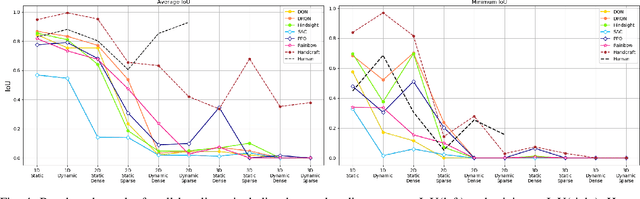
We need intelligent robots for mobile construction, the process of navigating in an environment and modifying its structure according to a geometric design. In this task, a major robot vision and learning challenge is how to exactly achieve the design without GPS, due to the difficulty caused by the bi-directional coupling of accurate robot localization and navigation together with strategic environment manipulation. However, many existing robot vision and learning tasks such as visual navigation and robot manipulation address only one of these two coupled aspects. To stimulate the pursuit of a generic and adaptive solution, we reasonably simplify mobile construction as a partially observable Markov decision process (POMDP) in 1/2/3D grid worlds and benchmark the performance of a handcrafted policy with basic localization and planning, and state-of-the-art deep reinforcement learning (RL) methods. Our extensive experiments show that the coupling makes this problem very challenging for those methods, and emphasize the need for novel task-specific solutions.