Evolutionary Contrastive Distillation for Language Model Alignment

The ability of large language models (LLMs) to execute complex instructions is essential for their real-world applications. However, several recent studies indicate that LLMs struggle with challenging instructions. In this paper, we propose Evolutionary Contrastive Distillation (ECD), a novel method for generating high-quality synthetic preference data designed to enhance the complex instruction-following capability of language models. ECD generates data that specifically illustrates the difference between a response that successfully follows a set of complex instructions and a response that is high-quality, but nevertheless makes some subtle mistakes. This is done by prompting LLMs to progressively evolve simple instructions to more complex instructions. When the complexity of an instruction is increased, the original successful response to the original instruction becomes a "hard negative" response for the new instruction, mostly meeting requirements of the new instruction, but barely missing one or two. By pairing a good response with such a hard negative response, and employing contrastive learning algorithms such as DPO, we improve language models' ability to follow complex instructions. Empirically, we observe that our method yields a 7B model that exceeds the complex instruction-following performance of current SOTA 7B models and is competitive even with open-source 70B models.

HYPO: Hyperspherical Out-of-Distribution Generalization

Out-of-distribution (OOD) generalization is critical for machine learning models deployed in the real world. However, achieving this can be fundamentally challenging, as it requires the ability to learn invariant features across different domains or environments. In this paper, we propose a novel framework HYPO (HYPerspherical OOD generalization) that provably learns domain-invariant representations in a hyperspherical space. In particular, our hyperspherical learning algorithm is guided by intra-class variation and inter-class separation principles -- ensuring that features from the same class (across different training domains) are closely aligned with their class prototypes, while different class prototypes are maximally separated. We further provide theoretical justifications on how our prototypical learning objective improves the OOD generalization bound. Through extensive experiments on challenging OOD benchmarks, we demonstrate that our approach outperforms competitive baselines and achieves superior performance. Code is available at https://github.com/deeplearning-wisc/hypo.

Training OOD Detectors in their Natural Habitats

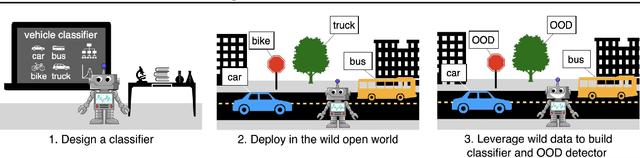
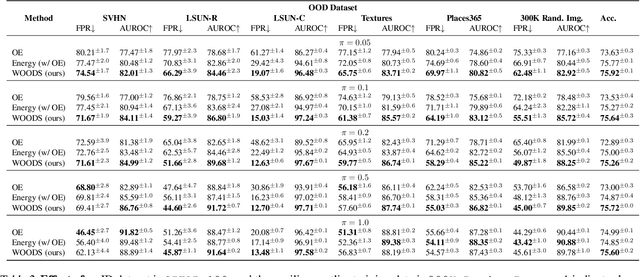
Out-of-distribution (OOD) detection is important for machine learning models deployed in the wild. Recent methods use auxiliary outlier data to regularize the model for improved OOD detection. However, these approaches make a strong distributional assumption that the auxiliary outlier data is completely separable from the in-distribution (ID) data. In this paper, we propose a novel framework that leverages wild mixture data -- that naturally consists of both ID and OOD samples. Such wild data is abundant and arises freely upon deploying a machine learning classifier in their \emph{natural habitats}. Our key idea is to formulate a constrained optimization problem and to show how to tractably solve it. Our learning objective maximizes the OOD detection rate, subject to constraints on the classification error of ID data and on the OOD error rate of ID examples. We extensively evaluate our approach on common OOD detection tasks and demonstrate superior performance.

GALAXY: Graph-based Active Learning at the Extreme

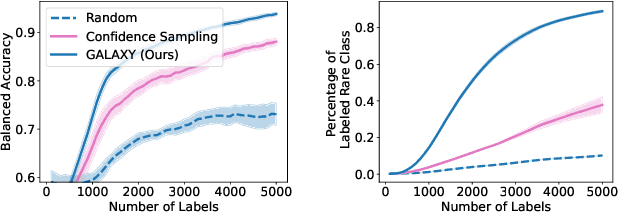
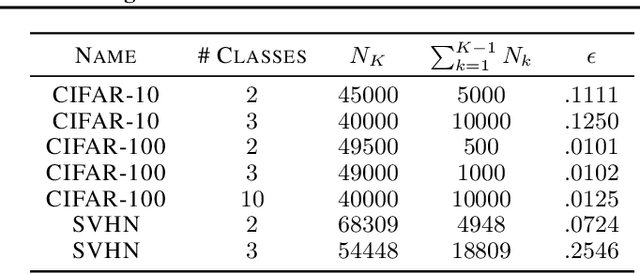
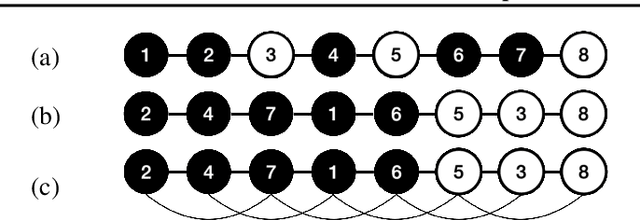
Active learning is a label-efficient approach to train highly effective models while interactively selecting only small subsets of unlabelled data for labelling and training. In "open world" settings, the classes of interest can make up a small fraction of the overall dataset -- most of the data may be viewed as an out-of-distribution or irrelevant class. This leads to extreme class-imbalance, and our theory and methods focus on this core issue. We propose a new strategy for active learning called GALAXY (Graph-based Active Learning At the eXtrEme), which blends ideas from graph-based active learning and deep learning. GALAXY automatically and adaptively selects more class-balanced examples for labeling than most other methods for active learning. Our theory shows that GALAXY performs a refined form of uncertainty sampling that gathers a much more class-balanced dataset than vanilla uncertainty sampling. Experimentally, we demonstrate GALAXY's superiority over existing state-of-art deep active learning algorithms in unbalanced vision classification settings generated from popular datasets.

Practical, Provably-Correct Interactive Learning in the Realizable Setting: The Power of True Believers

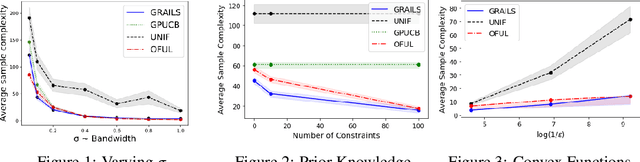
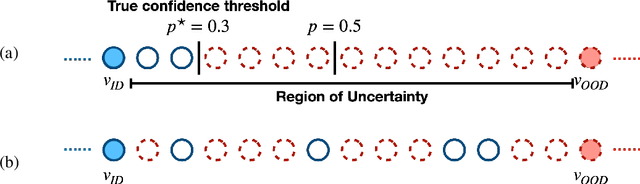
We consider interactive learning in the realizable setting and develop a general framework to handle problems ranging from best arm identification to active classification. We begin our investigation with the observation that agnostic algorithms \emph{cannot} be minimax-optimal in the realizable setting. Hence, we design novel computationally efficient algorithms for the realizable setting that match the minimax lower bound up to logarithmic factors and are general-purpose, accommodating a wide variety of function classes including kernel methods, H{\"o}lder smooth functions, and convex functions. The sample complexities of our algorithms can be quantified in terms of well-known quantities like the extended teaching dimension and haystack dimension. However, unlike algorithms based directly on those combinatorial quantities, our algorithms are computationally efficient. To achieve computational efficiency, our algorithms sample from the version space using Monte Carlo "hit-and-run" algorithms instead of maintaining the version space explicitly. Our approach has two key strengths. First, it is simple, consisting of two unifying, greedy algorithms. Second, our algorithms have the capability to seamlessly leverage prior knowledge that is often available and useful in practice. In addition to our new theoretical results, we demonstrate empirically that our algorithms are competitive with Gaussian process UCB methods.

Near Instance Optimal Model Selection for Pure Exploration Linear Bandits

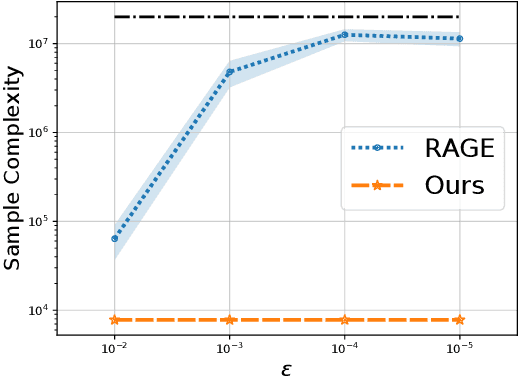
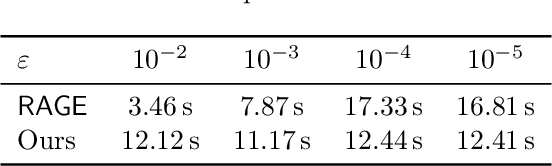
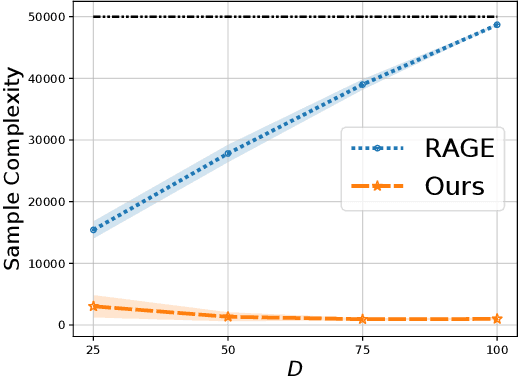
The model selection problem in the pure exploration linear bandit setting is introduced and studied in both the fixed confidence and fixed budget settings. The model selection problem considers a nested sequence of hypothesis classes of increasing complexities. Our goal is to automatically adapt to the instance-dependent complexity measure of the smallest hypothesis class containing the true model, rather than suffering from the complexity measure related to the largest hypothesis class. We provide evidence showing that a standard doubling trick over dimension fails to achieve the optimal instance-dependent sample complexity. Our algorithms define a new optimization problem based on experimental design that leverages the geometry of the action set to efficiently identify a near-optimal hypothesis class. Our fixed budget algorithm uses a novel application of a selection-validation trick in bandits. This provides a new method for the understudied fixed budget setting in linear bandits (even without the added challenge of model selection). We further generalize the model selection problem to the misspecified regime, adapting our algorithms in both fixed confidence and fixed budget settings.

Improved Algorithms for Agnostic Pool-based Active Classification

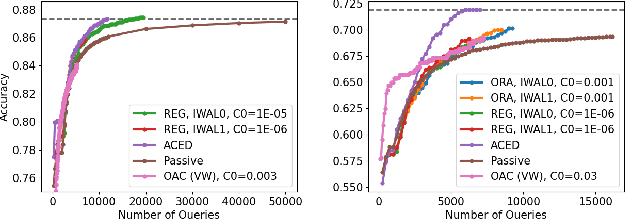
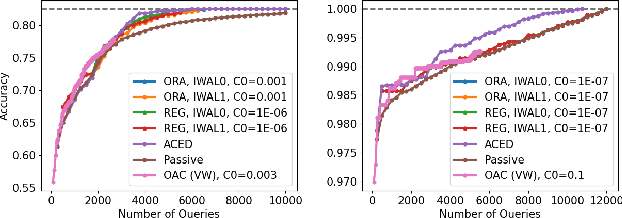
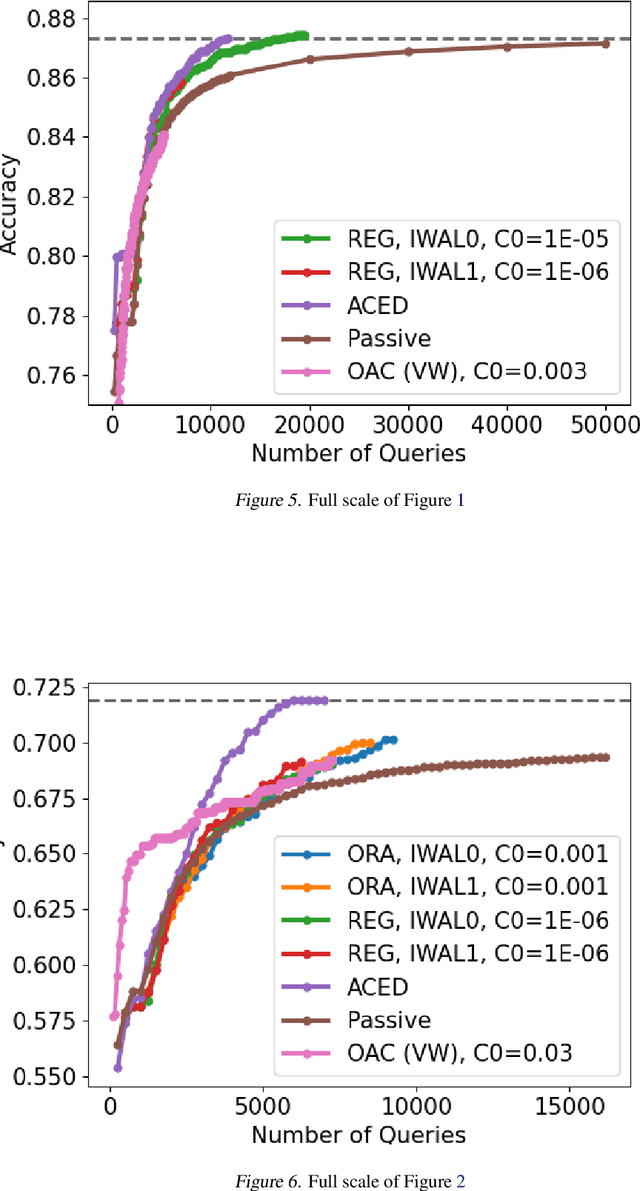
We consider active learning for binary classification in the agnostic pool-based setting. The vast majority of works in active learning in the agnostic setting are inspired by the CAL algorithm where each query is uniformly sampled from the disagreement region of the current version space. The sample complexity of such algorithms is described by a quantity known as the disagreement coefficient which captures both the geometry of the hypothesis space as well as the underlying probability space. To date, the disagreement coefficient has been justified by minimax lower bounds only, leaving the door open for superior instance dependent sample complexities. In this work we propose an algorithm that, in contrast to uniform sampling over the disagreement region, solves an experimental design problem to determine a distribution over examples from which to request labels. We show that the new approach achieves sample complexity bounds that are never worse than the best disagreement coefficient-based bounds, but in specific cases can be dramatically smaller. From a practical perspective, the proposed algorithm requires no hyperparameters to tune (e.g., to control the aggressiveness of sampling), and is computationally efficient by means of assuming access to an empirical risk minimization oracle (without any constraints). Empirically, we demonstrate that our algorithm is superior to state of the art agnostic active learning algorithms on image classification datasets.

High-Dimensional Experimental Design and Kernel Bandits

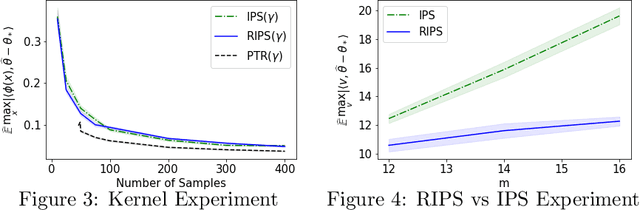
In recent years methods from optimal linear experimental design have been leveraged to obtain state of the art results for linear bandits. A design returned from an objective such as $G$-optimal design is actually a probability distribution over a pool of potential measurement vectors. Consequently, one nuisance of the approach is the task of converting this continuous probability distribution into a discrete assignment of $N$ measurements. While sophisticated rounding techniques have been proposed, in $d$ dimensions they require $N$ to be at least $d$, $d \log(\log(d))$, or $d^2$ based on the sub-optimality of the solution. In this paper we are interested in settings where $N$ may be much less than $d$, such as in experimental design in an RKHS where $d$ may be effectively infinite. In this work, we propose a rounding procedure that frees $N$ of any dependence on the dimension $d$, while achieving nearly the same performance guarantees of existing rounding procedures. We evaluate the procedure against a baseline that projects the problem to a lower dimensional space and performs rounding which requires $N$ to just be at least a notion of the effective dimension. We also leverage our new approach in a new algorithm for kernelized bandits to obtain state of the art results for regret minimization and pure exploration. An advantage of our approach over existing UCB-like approaches is that our kernel bandit algorithms are also robust to model misspecification.

Experimental Design for Regret Minimization in Linear Bandits

In this paper we propose a novel experimental design-based algorithm to minimize regret in online stochastic linear and combinatorial bandits. While existing literature tends to focus on optimism-based algorithms--which have been shown to be suboptimal in many cases--our approach carefully plans which action to take by balancing the tradeoff between information gain and reward, overcoming the failures of optimism. In addition, we leverage tools from the theory of suprema of empirical processes to obtain regret guarantees that scale with the Gaussian width of the action set, avoiding wasteful union bounds. We provide state-of-the-art finite time regret guarantees and show that our algorithm can be applied in both the bandit and semi-bandit feedback regime. In the combinatorial semi-bandit setting, we show that our algorithm is computationally efficient and relies only on calls to a linear maximization oracle. In addition, we show that with slight modification our algorithm can be used for pure exploration, obtaining state-of-the-art pure exploration guarantees in the semi-bandit setting. Finally, we provide, to the best of our knowledge, the first example where optimism fails in the semi-bandit regime, and show that in this setting our algorithm succeeds.

An Empirical Process Approach to the Union Bound: Practical Algorithms for Combinatorial and Linear Bandits

This paper proposes near-optimal algorithms for the pure-exploration linear bandit problem in the fixed confidence and fixed budget settings. Leveraging ideas from the theory of suprema of empirical processes, we provide an algorithm whose sample complexity scales with the geometry of the instance and avoids an explicit union bound over the number of arms. Unlike previous approaches which sample based on minimizing a worst-case variance (e.g. G-optimal design), we define an experimental design objective based on the Gaussian-width of the underlying arm set. We provide a novel lower bound in terms of this objective that highlights its fundamental role in the sample complexity. The sample complexity of our fixed confidence algorithm matches this lower bound, and in addition is computationally efficient for combinatorial classes, e.g. shortest-path, matchings and matroids, where the arm sets can be exponentially large in the dimension. Finally, we propose the first algorithm for linear bandits in the the fixed budget setting. Its guarantee matches our lower bound up to logarithmic factors.