Global Minimizers of $\ell^p$-Regularized Objectives Yield the Sparsest ReLU Neural Networks

Overparameterized neural networks can interpolate a given dataset in many different ways, prompting the fundamental question: which among these solutions should we prefer, and what explicit regularization strategies will provably yield these solutions? This paper addresses the challenge of finding the sparsest interpolating ReLU network -- i.e., the network with the fewest nonzero parameters or neurons -- a goal with wide-ranging implications for efficiency, generalization, interpretability, theory, and model compression. Unlike post hoc pruning approaches, we propose a continuous, almost-everywhere differentiable training objective whose global minima are guaranteed to correspond to the sparsest single-hidden-layer ReLU networks that fit the data. This result marks a conceptual advance: it recasts the combinatorial problem of sparse interpolation as a smooth optimization task, potentially enabling the use of gradient-based training methods. Our objective is based on minimizing $\ell^p$ quasinorms of the weights for $0 < p < 1$, a classical sparsity-promoting strategy in finite-dimensional settings. However, applying these ideas to neural networks presents new challenges: the function class is infinite-dimensional, and the weights are learned using a highly nonconvex objective. We prove that, under our formulation, global minimizers correspond exactly to sparsest solutions. Our work lays a foundation for understanding when and how continuous sparsity-inducing objectives can be leveraged to recover sparse networks through training.

The Effects of Multi-Task Learning on ReLU Neural Network Functions

This paper studies the properties of solutions to multi-task shallow ReLU neural network learning problems, wherein the network is trained to fit a dataset with minimal sum of squared weights. Remarkably, the solutions learned for each individual task resemble those obtained by solving a kernel method, revealing a novel connection between neural networks and kernel methods. It is known that single-task neural network training problems are equivalent to minimum norm interpolation problem in a non-Hilbertian Banach space, and that the solutions of such problems are generally non-unique. In contrast, we prove that the solutions to univariate-input, multi-task neural network interpolation problems are almost always unique, and coincide with the solution to a minimum-norm interpolation problem in a Sobolev (Reproducing Kernel) Hilbert Space. We also demonstrate a similar phenomenon in the multivariate-input case; specifically, we show that neural network learning problems with large numbers of diverse tasks are approximately equivalent to an $\ell^2$ (Hilbert space) minimization problem over a fixed kernel determined by the optimal neurons.

Training OOD Detectors in their Natural Habitats

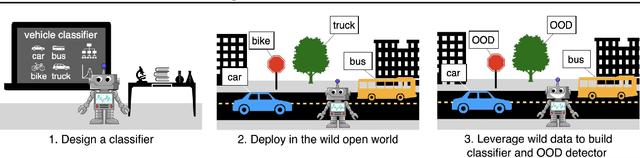
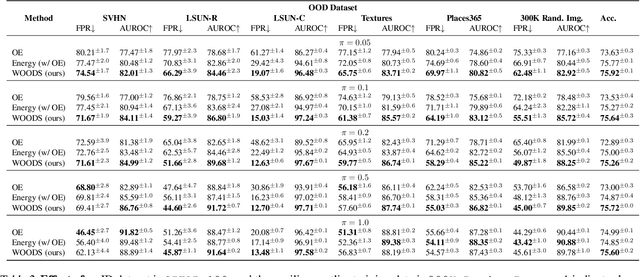
Out-of-distribution (OOD) detection is important for machine learning models deployed in the wild. Recent methods use auxiliary outlier data to regularize the model for improved OOD detection. However, these approaches make a strong distributional assumption that the auxiliary outlier data is completely separable from the in-distribution (ID) data. In this paper, we propose a novel framework that leverages wild mixture data -- that naturally consists of both ID and OOD samples. Such wild data is abundant and arises freely upon deploying a machine learning classifier in their \emph{natural habitats}. Our key idea is to formulate a constrained optimization problem and to show how to tractably solve it. Our learning objective maximizes the OOD detection rate, subject to constraints on the classification error of ID data and on the OOD error rate of ID examples. We extensively evaluate our approach on common OOD detection tasks and demonstrate superior performance.