Detect, Retrieve, Comprehend: A Flexible Framework for Zero-Shot Document-Level Question Answering

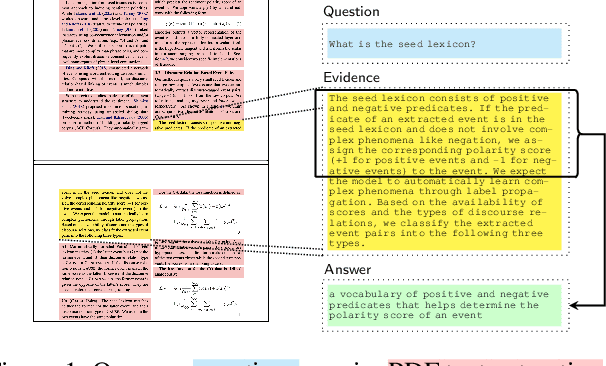
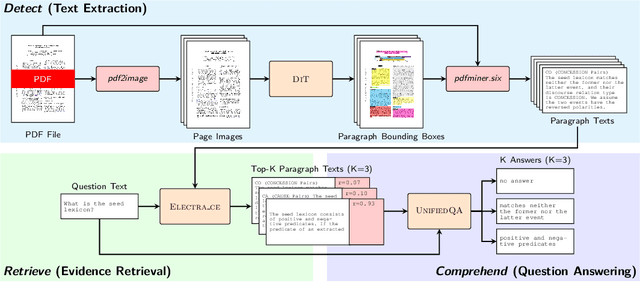
Businesses generate thousands of documents that communicate their strategic vision and provide details of key products, services, entities, and processes. Knowledge workers then face the laborious task of reading these documents to identify, extract, and synthesize information relevant to their organizational goals. To automate information gathering, question answering (QA) offers a flexible framework where human-posed questions can be adapted to extract diverse knowledge. Finetuning QA systems requires access to labeled data (tuples of context, question, and answer). However, data curation for document QA is uniquely challenging because the context (i.e., answer evidence passage) needs to be retrieved from potentially long, ill-formatted documents. Existing QA datasets sidestep this challenge by providing short, well-defined contexts that are unrealistic in real-world applications. We present a three-stage document QA approach: (1) text extraction from PDF; (2) evidence retrieval from extracted texts to form well-posed contexts; (3) QA to extract knowledge from contexts to return high-quality answers - extractive, abstractive, or Boolean. Using QASPER as a surrogate to our proprietary data, our detect-retrieve-comprehend (DRC) system achieves a +6.25 improvement in Answer-F1 over existing baselines while delivering superior context selection. Our results demonstrate that DRC holds tremendous promise as a flexible framework for practical document QA.

One for All: Simultaneous Metric and Preference Learning over Multiple Users

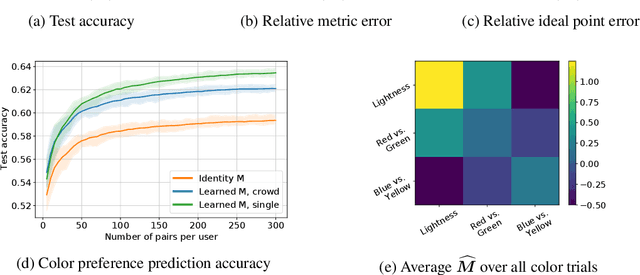
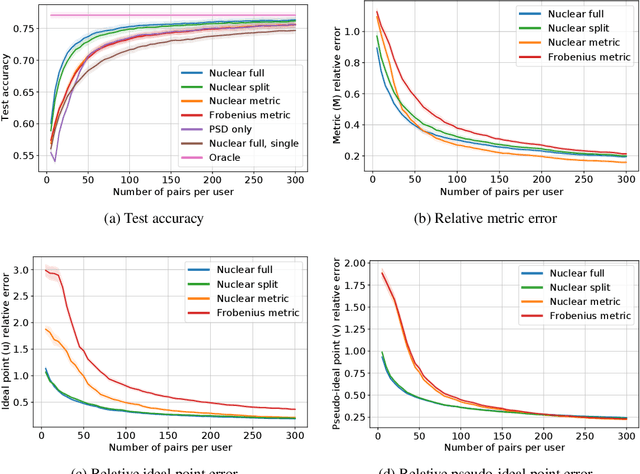
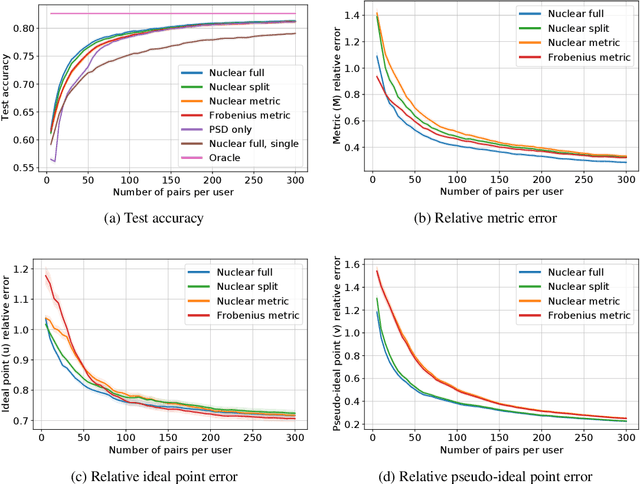
This paper investigates simultaneous preference and metric learning from a crowd of respondents. A set of items represented by $d$-dimensional feature vectors and paired comparisons of the form ``item $i$ is preferable to item $j$'' made by each user is given. Our model jointly learns a distance metric that characterizes the crowd's general measure of item similarities along with a latent ideal point for each user reflecting their individual preferences. This model has the flexibility to capture individual preferences, while enjoying a metric learning sample cost that is amortized over the crowd. We first study this problem in a noiseless, continuous response setting (i.e., responses equal to differences of item distances) to understand the fundamental limits of learning. Next, we establish prediction error guarantees for noisy, binary measurements such as may be collected from human respondents, and show how the sample complexity improves when the underlying metric is low-rank. Finally, we establish recovery guarantees under assumptions on the response distribution. We demonstrate the performance of our model on both simulated data and on a dataset of color preference judgements across a large number of users.

Benign Overparameterization in Membership Inference with Early Stopping

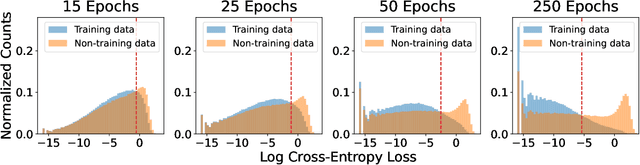
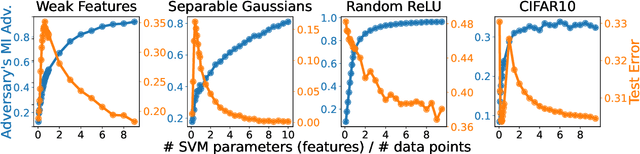
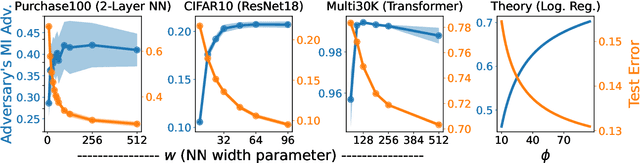
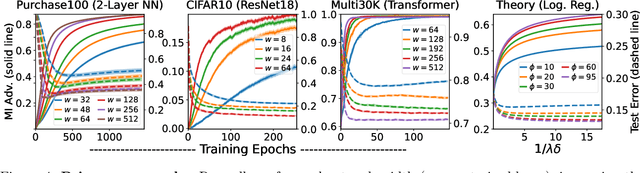
Does a neural network's privacy have to be at odds with its accuracy? In this work, we study the effects the number of training epochs and parameters have on a neural network's vulnerability to membership inference (MI) attacks, which aim to extract potentially private information about the training data. We first demonstrate how the number of training epochs and parameters individually induce a privacy-utility trade-off: more of either improves generalization performance at the expense of lower privacy. However, remarkably, we also show that jointly tuning both can eliminate this privacy-utility trade-off. Specifically, with careful tuning of the number of training epochs, more overparameterization can increase model privacy for fixed generalization error. To better understand these phenomena theoretically, we develop a powerful new leave-one-out analysis tool to study the asymptotic behavior of linear classifiers and apply it to characterize the sample-specific loss threshold MI attack in high-dimensional logistic regression. For practitioners, we introduce a low-overhead procedure to estimate MI risk and tune the number of training epochs to guard against MI attacks.

An Experimental Design Approach for Regret Minimization in Logistic Bandits

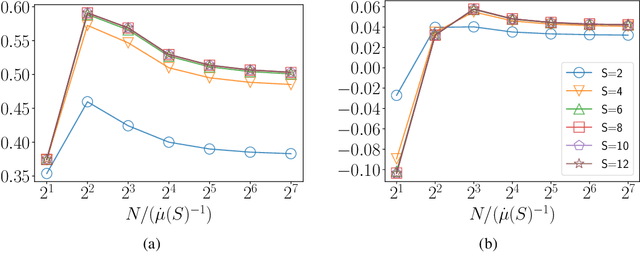
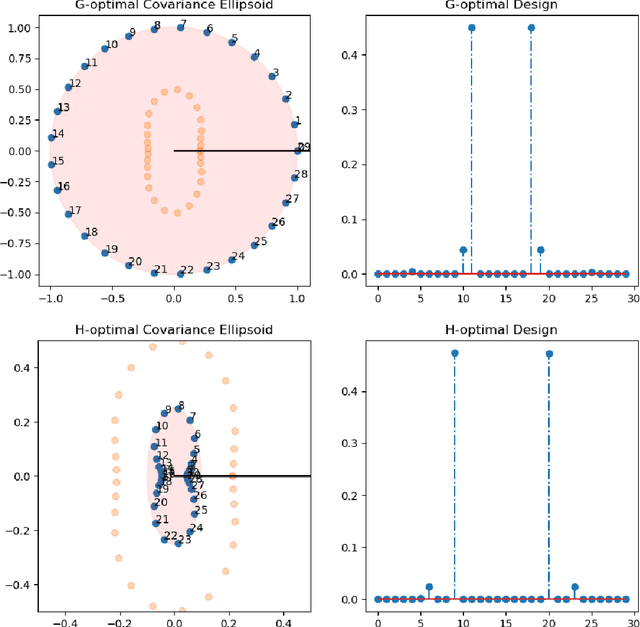
In this work we consider the problem of regret minimization for logistic bandits. The main challenge of logistic bandits is reducing the dependence on a potentially large problem dependent constant $\kappa$ that can at worst scale exponentially with the norm of the unknown parameter $\theta_{\ast}$. Abeille et al. (2021) have applied self-concordance of the logistic function to remove this worst-case dependence providing regret guarantees like $O(d\log^2(\kappa)\sqrt{\dot\mu T}\log(|\mathcal{X}|))$ where $d$ is the dimensionality, $T$ is the time horizon, and $\dot\mu$ is the variance of the best-arm. This work improves upon this bound in the fixed arm setting by employing an experimental design procedure that achieves a minimax regret of $O(\sqrt{d \dot\mu T\log(|\mathcal{X}|)})$. Our regret bound in fact takes a tighter instance (i.e., gap) dependent regret bound for the first time in logistic bandits. We also propose a new warmup sampling algorithm that can dramatically reduce the lower order term in the regret in general and prove that it can replace the lower order term dependency on $\kappa$ to $\log^2(\kappa)$ for some instances. Finally, we discuss the impact of the bias of the MLE on the logistic bandit problem, providing an example where $d^2$ lower order regret (cf., it is $d$ for linear bandits) may not be improved as long as the MLE is used and how bias-corrected estimators may be used to make it closer to $d$.

Parameters or Privacy: A Provable Tradeoff Between Overparameterization and Membership Inference

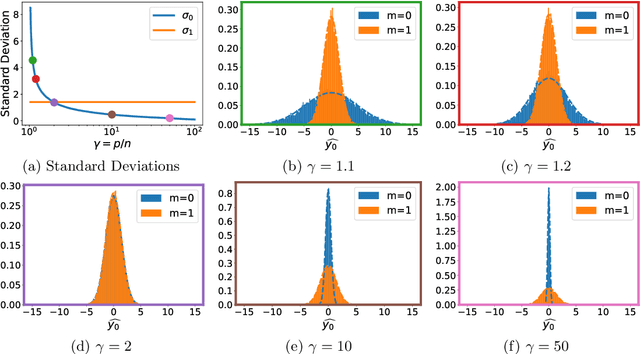
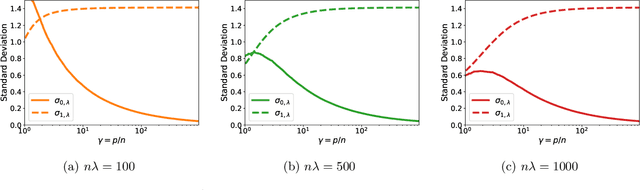
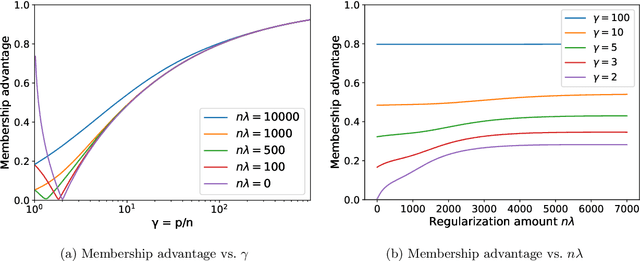
A surprising phenomenon in modern machine learning is the ability of a highly overparameterized model to generalize well (small error on the test data) even when it is trained to memorize the training data (zero error on the training data). This has led to an arms race towards increasingly overparameterized models (c.f., deep learning). In this paper, we study an underexplored hidden cost of overparameterization: the fact that overparameterized models are more vulnerable to privacy attacks, in particular the membership inference attack that predicts the (potentially sensitive) examples used to train a model. We significantly extend the relatively few empirical results on this problem by theoretically proving for an overparameterized linear regression model with Gaussian data that the membership inference vulnerability increases with the number of parameters. Moreover, a range of empirical studies indicates that more complex, nonlinear models exhibit the same behavior. Finally, we study different methods for mitigating such attacks in the overparameterized regime, such as noise addition and regularization, and conclude that simply reducing the parameters of an overparameterized model is an effective strategy to protect it from membership inference without greatly decreasing its generalization error.

Practical, Provably-Correct Interactive Learning in the Realizable Setting: The Power of True Believers

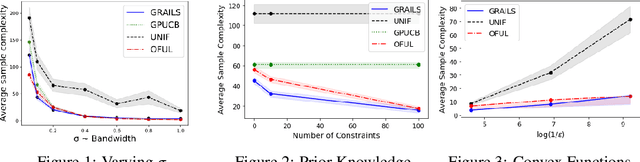
We consider interactive learning in the realizable setting and develop a general framework to handle problems ranging from best arm identification to active classification. We begin our investigation with the observation that agnostic algorithms \emph{cannot} be minimax-optimal in the realizable setting. Hence, we design novel computationally efficient algorithms for the realizable setting that match the minimax lower bound up to logarithmic factors and are general-purpose, accommodating a wide variety of function classes including kernel methods, H{\"o}lder smooth functions, and convex functions. The sample complexities of our algorithms can be quantified in terms of well-known quantities like the extended teaching dimension and haystack dimension. However, unlike algorithms based directly on those combinatorial quantities, our algorithms are computationally efficient. To achieve computational efficiency, our algorithms sample from the version space using Monte Carlo "hit-and-run" algorithms instead of maintaining the version space explicitly. Our approach has two key strengths. First, it is simple, consisting of two unifying, greedy algorithms. Second, our algorithms have the capability to seamlessly leverage prior knowledge that is often available and useful in practice. In addition to our new theoretical results, we demonstrate empirically that our algorithms are competitive with Gaussian process UCB methods.

Nearly Optimal Algorithms for Level Set Estimation

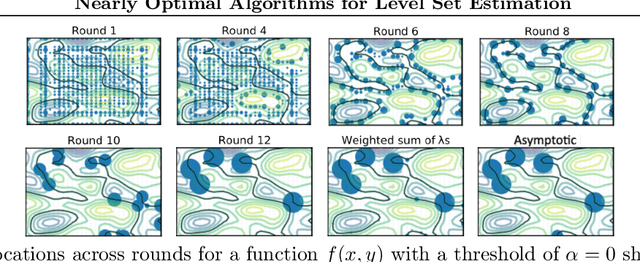
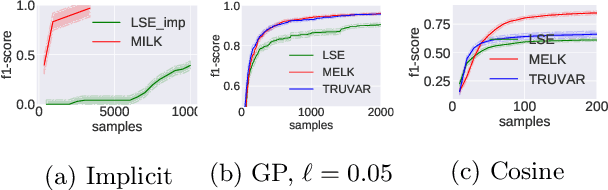
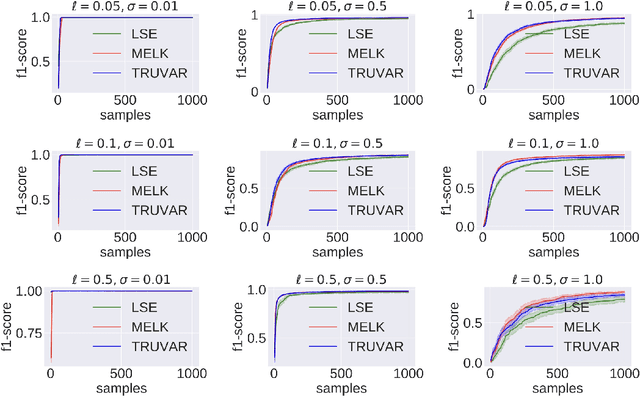
The level set estimation problem seeks to find all points in a domain ${\cal X}$ where the value of an unknown function $f:{\cal X}\rightarrow \mathbb{R}$ exceeds a threshold $\alpha$. The estimation is based on noisy function evaluations that may be acquired at sequentially and adaptively chosen locations in ${\cal X}$. The threshold value $\alpha$ can either be \emph{explicit} and provided a priori, or \emph{implicit} and defined relative to the optimal function value, i.e. $\alpha = (1-\epsilon)f(x_\ast)$ for a given $\epsilon > 0$ where $f(x_\ast)$ is the maximal function value and is unknown. In this work we provide a new approach to the level set estimation problem by relating it to recent adaptive experimental design methods for linear bandits in the Reproducing Kernel Hilbert Space (RKHS) setting. We assume that $f$ can be approximated by a function in the RKHS up to an unknown misspecification and provide novel algorithms for both the implicit and explicit cases in this setting with strong theoretical guarantees. Moreover, in the linear (kernel) setting, we show that our bounds are nearly optimal, namely, our upper bounds match existing lower bounds for threshold linear bandits. To our knowledge this work provides the first instance-dependent, non-asymptotic upper bounds on sample complexity of level-set estimation that match information theoretic lower bounds.

NFT-K: Non-Fungible Tangent Kernels

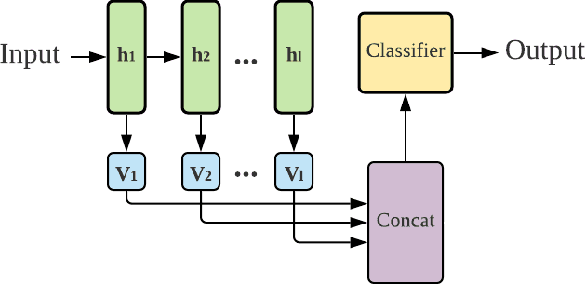
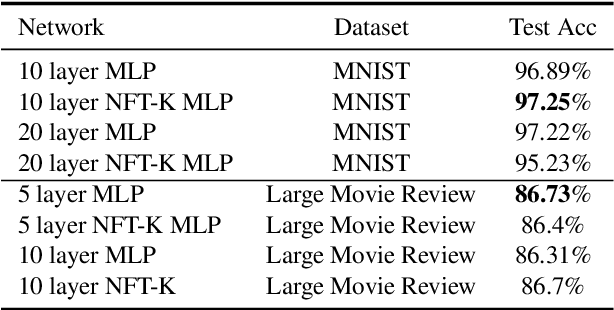
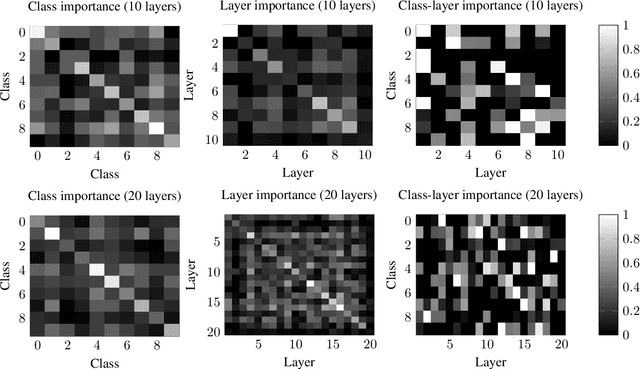
Deep neural networks have become essential for numerous applications due to their strong empirical performance such as vision, RL, and classification. Unfortunately, these networks are quite difficult to interpret, and this limits their applicability in settings where interpretability is important for safety, such as medical imaging. One type of deep neural network is neural tangent kernel that is similar to a kernel machine that provides some aspect of interpretability. To further contribute interpretability with respect to classification and the layers, we develop a new network as a combination of multiple neural tangent kernels, one to model each layer of the deep neural network individually as opposed to past work which attempts to represent the entire network via a single neural tangent kernel. We demonstrate the interpretability of this model on two datasets, showing that the multiple kernels model elucidates the interplay between the layers and predictions.

Nearest Neighbor Search Under Uncertainty

Nearest Neighbor Search (NNS) is a central task in knowledge representation, learning, and reasoning. There is vast literature on efficient algorithms for constructing data structures and performing exact and approximate NNS. This paper studies NNS under Uncertainty (NNSU). Specifically, consider the setting in which an NNS algorithm has access only to a stochastic distance oracle that provides a noisy, unbiased estimate of the distance between any pair of points, rather than the exact distance. This models many situations of practical importance, including NNS based on human similarity judgements, physical measurements, or fast, randomized approximations to exact distances. A naive approach to NNSU could employ any standard NNS algorithm and repeatedly query and average results from the stochastic oracle (to reduce noise) whenever it needs a pairwise distance. The problem is that a sufficient number of repeated queries is unknown in advance; e.g., a point maybe distant from all but one other point (crude distance estimates suffice) or it may be close to a large number of other points (accurate estimates are necessary). This paper shows how ideas from cover trees and multi-armed bandits can be leveraged to develop an NNSU algorithm that has optimal dependence on the dataset size and the (unknown)geometry of the dataset.

Finding All ε-Good Arms in Stochastic Bandits

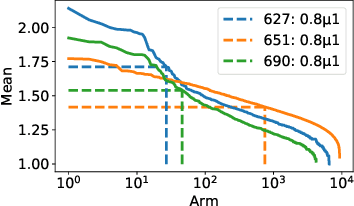
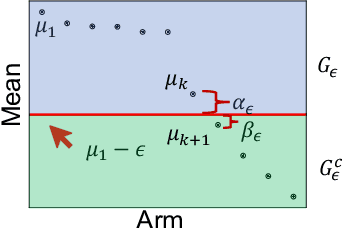
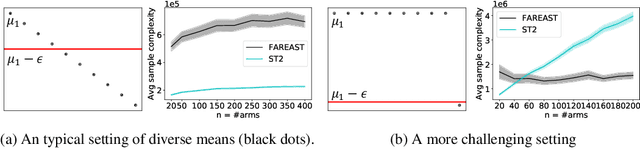
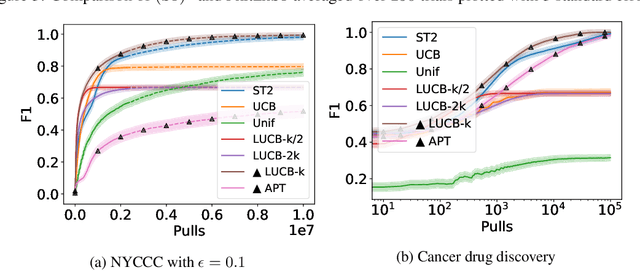
The pure-exploration problem in stochastic multi-armed bandits aims to find one or more arms with the largest (or near largest) means. Examples include finding an {\epsilon}-good arm, best-arm identification, top-k arm identification, and finding all arms with means above a specified threshold. However, the problem of finding all {\epsilon}-good arms has been overlooked in past work, although arguably this may be the most natural objective in many applications. For example, a virologist may conduct preliminary laboratory experiments on a large candidate set of treatments and move all {\epsilon}-good treatments into more expensive clinical trials. Since the ultimate clinical efficacy is uncertain, it is important to identify all {\epsilon}-good candidates. Mathematically, the all-{\epsilon}-good arm identification problem presents significant new challenges and surprises that do not arise in the pure-exploration objectives studied in the past. We introduce two algorithms to overcome these and demonstrate their great empirical performance on a large-scale crowd-sourced dataset of 2.2M ratings collected by the New Yorker Caption Contest as well as a dataset testing hundreds of possible cancer drugs.